Herramientas de usuario
Barra lateral
clase:iabd:pia:2eval:tema07.metricas
Tabla de Contenidos
7.e Métricas clasificación (Bayes)
En este apartado vamos a ver las métricas asociadas a problemas de clasificación en las redes neuronales. Como el tema es muy amplio son muchas, seguiremos en 7.f Más métricas de clasificación y 7.g Apéndices.
Métricas de clasificación con 2 posibles valores
Clasificación con 2 posibles valores es cuando la salida de nuestra red neuronal solo puede tener 2 posibles valores.
Antes de entrar a ver las métricas , es necesario entender lo que son:
- True Positives o TP o Verdaderos Positivos: Cuando la red neuronal a predicho que es positivo y realmente es positivo
- True Negatives o TN o Verdaderos Negativos: Cuando la red neuronal a predicho que es negativo y realmente es negativo
- False Positives o FP o Falsos positivos: Cuando la red neuronal a predicho que es positivo pero es falso ya que realmente es negativo
- False Negatives o FN o Falsos negativos: Cuando la red neuronal a predicho que es negativo pero es falso ya que realmente es positivo
Estos 4 valores se pueden representar en una matriz llamada matriz de confusión.
Para distinguir:
- predicho que es positivo de realmente es positivo
- predicho que es negativo de realmente es negativo
para ello vamos a seguir la siguiente nomenclatura basada en un ejemplo de red neuronal que detectara enfermedades:
- Predicho que es positivo=Positivo
- Predicho que es negativo=Negativo
- Realmente es positivo=Enfermo
- Realmente es negativo=Sano
Por lo que podemos rehacer la lista inicial como:
- TP: Positivo y Enfermo
- TN: Negativo y Sano
- FP: Positivo y Sano
- FN: Negativo y Enfermo
| Predicción | |||
|---|---|---|---|
| Positivo | Negativo | ||
| Realidad | Enfermo | TP | FN |
| Sano | FP | TN | |
Más información:
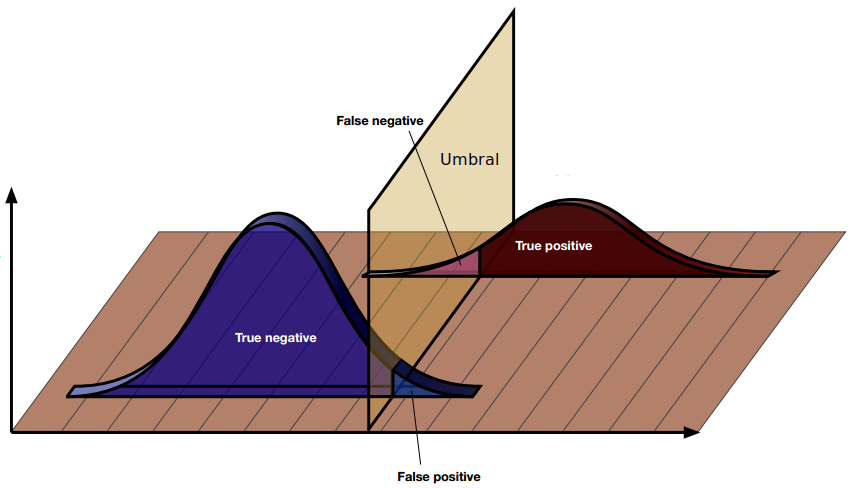
Umbral o Threshold
En la clasificación binaria los posibles valores son 1 y 0 o True y False. Sin embargo nuestra red neuronal suele sacar un valor entre 0 y 1.
A ese valor se le llama y_score y en función de un threshold lo transformamos en el valor predicho o y_pred.
Si el valor del score es mayor que el threshold el valor predicho será un True mientras que si el valor del score es menor que el threshold el valor predicho será un False
Veamos un ejemplo de ello:
y_score=np.array([0.27, 0.45, 0.76, 0.55, 0.28, 0.04, 0.34,0.4, 0.66, 0.88, 0.94,0.47,0.2]) y_pred=y_score>0.5 print(y_pred)
Siendo el resultado
[False False True True False False False False True True True False False]
Por ello la mayoría de nuestras métricas son dependientes del valor que indiquemos de threshold. Excepto la métrica de AUC que es independiente del valor de threshold.
Un ejemplo de lo que acabamos de ver está en las métricas de f1-score y AUC de sklearn.
En https://scikit-learn.org/stable/modules/generated/sklearn.metrics.f1_score.html los parámetros de entrada son y_true e y_pred
mientras que en https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_auc_score.html los parámetros de entrada son y_true e y_score ya que no necesita el umbral
Probabilidad condicional
La probabilidad condicional se expresa de la siguiente forma $P(A|B)$ que significa , la probabilidad de que ocurra A sabiendo que ya ocurrido B. ¿Y que tiene que ver ésto con las métricas? Realmente las métricas se pueden expresar como probabilidades condicionales. Lo bueno de usar probabilidades condicionales es que se entienden mejor.
Para explicar las métricas vamos a imaginar los test de COVID que comprobamos en las farmacias , que nos decían si teníamos o no COVID. El ejemplo es igual que si fuera una red neuronal que dado una radiografía nos dijera si teníamos o no COVID. Pero se usa el test de farmacia de COVID para hacer más comprensible la explicación.
Para poner la probabilidad condicional vamos a con la nomenclatura anterior
- $Positivo$: El test ha dado un valor positivo. Umbral >= 0.5
- $Negativo$: El test ha dado un valor negativo. Umbral < 0.5
- $Enfermo$: El paciente está enfermo ya que se ha usado el test de referencia (distinta a nuestro test) que sabemos que acierta el 100% de las veces.
- $Sano$: El paciente está sano ya que se ha usado el test de referencia (distinta a nuestro test) que sabemos que acierta el 100% de las veces.
Veamos ahora unas probabilidades condicionales.
- $P(Positivo|Enfermo)$: Sabiendo que una persona ya está enferma y le hacemos el test, obtendríamos la probabilidad de que el test de positivo para esa persona.
- $P(Enfermo|Positivo)$: Sabiendo que la persona ha dado positivo en el test obtendríamos la probabilidad de que la persona esté enferma.
Detengámonos un momento. ¿Cual de las 2 probabilidades nos interesa?. $P(Positivo|Enferma)$ o $P(Enferma|Positivo)$. Si lo pensamos , ¿para que queremos saber $P(Positivo|Enferma)$? Si ya sabemos que la persona está enferma, ¿para que querríamos usar el test? ¡¡Ya sabemos que está enferma!!!! Así que realmente nos interesa $P(Enferma|Positivo)$
Cálculo de las métricas
Pongamos ahora todas las combinaciones de probabilidades posibles de las métricas que realmente nos interesan.
- $P(Enfermo|Positivo)$: Sabiendo que es test da Positivo , obtendríamos la probabilidad de que la persona esté Enfermo.
- $P(Sano|Positivo)$: Sabiendo que es test da Positivo , obtendríamos la probabilidad de que la persona esté Sano.
- $P(Sano|Negativo)$: Sabiendo que es test da Negativo , obtendríamos la probabilidad de que la persona esté Sano.
- $P(Enfermo|Negativo)$: Sabiendo que es test da Negativo , obtendríamos la probabilidad de que la persona esté Enfermo.
Mientras que las 4 siguientes aparentemente no nos interesan lo más mínimo:
- $P(Positivo|Enfermo)$: Sabiendo que la persona esté Enfermo, obtendríamos la probabilidad de que el test de Positivo.
- $P(Negativo|Enfermo)$: Sabiendo que la persona esté Enfermo, obtendríamos la probabilidad de que el test de Negativo.
- $P(Negativo|Sano)$: Sabiendo que la persona esté Sano, obtendríamos la probabilidad de que el test de Negativo.
- $P(Positivo|Sano)$: Sabiendo que la persona esté Sano, obtendríamos la probabilidad de que el test de Positivo.
Volvamos a la matriz de confusión:
| Predicción | |||
|---|---|---|---|
| Positivo (PP) | Negativo (PN) | ||
| Realidad | Enfermo (P) | TP | FN |
| Sano (N) | FP | TN | |
$$ \begin{array} \\ E&=&TP+FN&=&Nº \; de \; enfermos \\ S&=&FP+TN&=&Nº \; de \; sanos \\ PP&=&TP+FP&=&Nº \; predichos \; positivos \\ PN&=&FN+TN&=&Nº \; predichos \; negativos \\ \end{array} $$
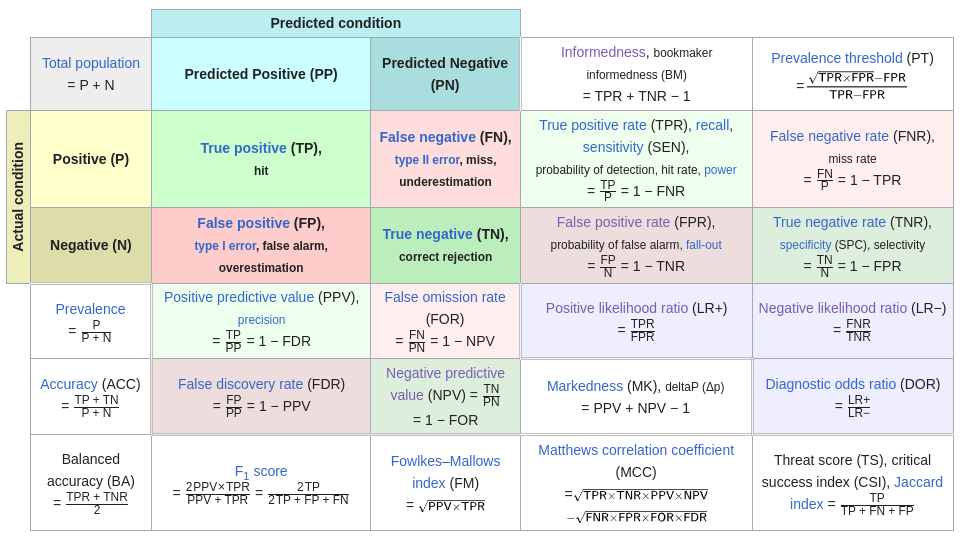
Y siendo un poco perspicaces podremos ver como se calculan las 8 probabilidades y los nombres que tienen:
$$
\begin{array}
\\
P(Enfermo|Positivo)&=&\frac{TP}{PP}&=&\frac{TP}{TP+FP}&=&Positive \; Predictive \; Value \; (PPV)&=&Precisión&
\\
P(Sano|Positivo)&=&\frac{FP}{PP}&=&\frac{FP}{TP+FP}&=&False \; Discovery \; Rate \; (FDR)&=&1-Precisión
\\
\\
P(Sano|Negativo)&=&\frac{TN}{PN}&=&\frac{TN}{FN+TN}&=&Negative \; Predictive \; Value \; (NPV)&&
\\
P(Enfermo|Negativo)&=&\frac{FP}{PN}&=&\frac{FP}{FN+TN}&=&False \; Omission \; Rate \; (FOR)&=&1-NPV
\\
\end{array}
$$
$$
\begin{array}
\\
P(Positivo|Enfermo)&=&\frac{TP}{E}&=&\frac{TP}{TP+FN}&=&True \; Positive \; Rate (TPR) &=&Sensibilidad
\\
P(Negativo|Enfermo)&=&\frac{FN}{E}&=&\frac{FN}{TP+FN}&=&False \; Negative \; Rate \; (FNR)&=&1-Sensibilidad
\\
\\
P(Negativo|Sano)&=&\frac{TN}{S}&=&\frac{TN}{FP+TN}&=&True \; Negative \; Rate (TNR) &=&Especificidad
\\
P(Positivo|Sano)&=&\frac{FP}{S}&=&\frac{FP}{FP+TN}&=&False \; Positive \; Rate \; (FPR)&=&1-Especificidad
\\
\end{array}
$$
| Predicción | |||||
|---|---|---|---|---|---|
| Positivo (PP) | Negativo (PN) | Métricas | |||
| Realidad | Enfermo (E) | TP | FN | $P(Positivo|Enfermo)=\frac{TP}{E}$ | $P(Negativo|Enfermo)=\frac{FN}{E}$ |
| Sano (S) | FP | TN | $P(Positivo|Sano)=\frac{FP}{S}$ | $P(Negativo|Sano)=\frac{TN}{S}$ | |
| Métricas | $P(Enfermo|Positivo)=\frac{TP}{PP}$ | $P(Enfermo|Negativo)=\frac{FN}{PN}$ | |||
| $P(Sano|Positivo)=\frac{FP}{PP}$ | $P(Sano|Negativo)=\frac{TN}{PN}$ | ||||
| Predicción | |||||
|---|---|---|---|---|---|
| Positivo (PP) | Negativo (PN) | Métricas | |||
| Realidad | Enfermo (E) | TP | FN | $TPR=\frac{TP}{E}$ | $FNR=\frac{FN}{E}$ |
| Sano (S) | FP | TN | $FPR=\frac{FP}{S}$ | $TNR=\frac{TN}{S}$ | |
| Métricas | $PPV=\frac{TP}{PP}$ | $FOR=\frac{FN}{PN}$ | |||
| $FDR=\frac{FP}{PP}$ | $NPV=\frac{TN}{PN}$ | ||||
| Predicción | |||||
|---|---|---|---|---|---|
| Positivo (PP) | Negativo (PN) | Métricas | |||
| Realidad | Enfermo (E) | TP | FN | $Sensibilidad=\frac{TP}{E}$ | $FNR=\frac{FN}{E}$ |
| Sano (S) | FP | TN | $FPR=\frac{FP}{S}$ | $Especificidad=\frac{TN}{S}$ | |
| Métricas | $Precisión=\frac{TP}{PP}$ | $FOR=\frac{FN}{PN}$ | |||
| $FDR=\frac{FP}{PP}$ | $NPV=\frac{TN}{PN}$ | ||||
Selección de métricas
Volvamos ahora a recapacitar otra vez sobre el significado de las métricas. En un test perfecto realmente lo que nos interesa es:
- $P(Enfermo|Positivo)=1$: Si el test da Positivo que la probabilidad de estar Enfermo sea 1.
- $P(Sano|Negativo)=1$: Si el test da Negativo que la probabilidad de estar Sano sea 1.
A esas 2 métricas se les llama:
- $P(Enfermo|Positivo)=Valor \; Predictivo \; Positivo \; (VPP)=Positive \; Predictive \; Value \; (PPV)=Precisión$
- $P(Sano|Negativo)=Valor \; Predictivo \; Negativo \; (VPN)=Negative \; Predictive \; Value \; (NPV)$
Se llaman así porque realmente son las 2 métricas que predicen si estás enfermo o sano cuando el test da positivo o negativo respectivamente. Y a la primera de ellas se le llama también precisión
Teorema de Bayes
El problema de calcular la precisión y el VPN es que sus valores dependen de la cantidad de enfermos y de sanos que tengamos al entrenar nuestra red. Por lo tanto del valor de E y S. Es decir que dependen de lo balanceados que tengamos nuestras clases.
Para calcular como de balanceadas están las clases se usa la $Prevalencia \; o \; P(Enfermo)$ , y es un dato muy importante que se calcula de la siguiente forma:
$$ Prevalencia=P(Enfermo)=\frac{TP+FN}{TP+FN+FP+TN}=\frac{E}{E+S} $$
Además están otras probabilidades que son:
$$ \begin{array} \\ P(Enfermo)&=&\frac{TP+FN}{TP+FN+FP+TN}&=&\frac{E}{E+S}&=&Prevalencia \\ P(Sano)&=&\frac{FP+TN}{TP+FN+FP+TN}&=&\frac{S}{E+S}&=&1-Prevalencia \\ P(Positivo)&=&\frac{TP+FP}{TP+FN+FP+TN}&=&\frac{PP}{PP+PN} \\ P(Negativo)&=&\frac{FN+TN}{TP+FN+FP+TN}&=&\frac{PN}{PP+PN}&=&1-P(Positivo) \end{array} $$
Recordar que: $$ E+S=PP+PN=Total $$
En la siguiente imagen vamos a obtener las métricas y vamos a ver como varían las métricas si aumenta o disminuye el número de positivos. Es decir vamos a ver como dependen la precisión y el VPN según la prevalencia.
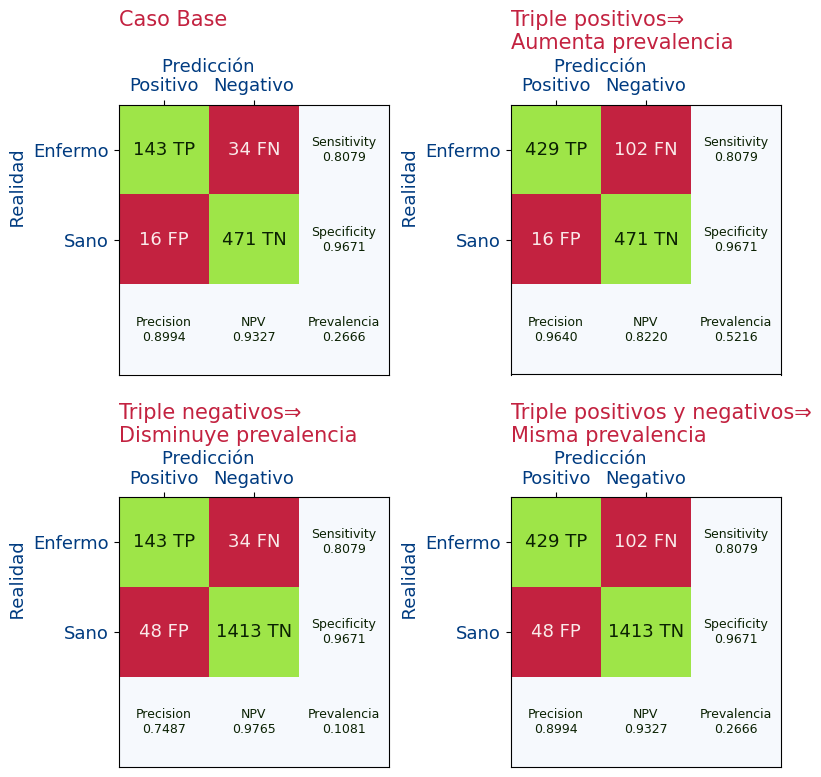
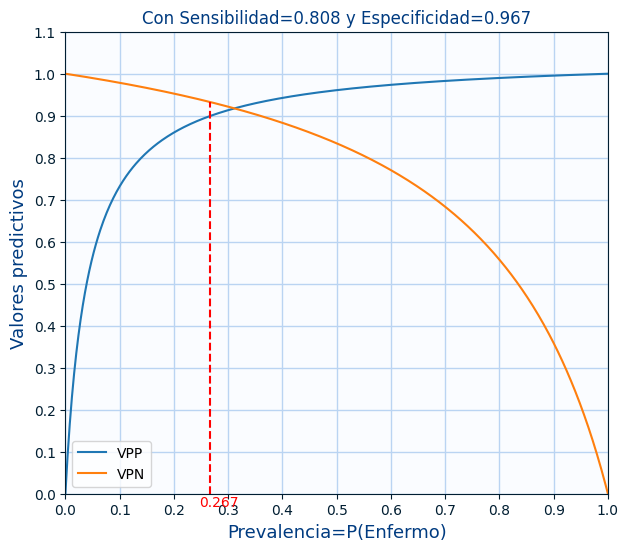
Vemos que si aumentamos el número de positivos (por lo tanto aumentando la prevalencia), se modifican las métricas de Precisión (VPP) y VPN de la siguiente forma:
- Si aumentamos la prevalencia:
- Mejora la precisión (VPP) ya que ha pasado de 0.89 a 0.96
- Empeora el VPN ya que ha pasado de 0.93 a 0.82
- Si disminuimos la prevalencia:
- Empeora la precisión (VPP) ya que ha pasado de 0.89 a 0.74
- Mejora el VPN ya que ha pasado de 0.93 a 0.97
En la gráfica se puede ver como varían el VPP y el VPN según la prevalencia. Y la línea roja es con la prevalencia de los datos.
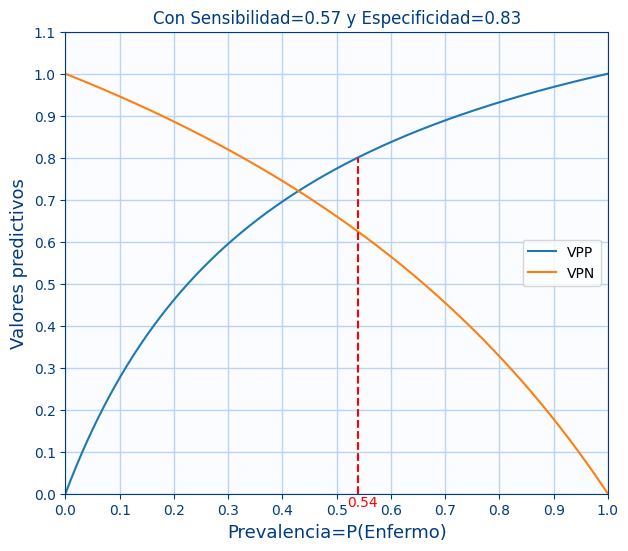
En la siguiente gráfica se ven varios ejemplos de $VPP$ y $VPN$ en función de la $Prevalencia$ para varios valores de $sensibilidad$ y la $especificidad$
Por lo tanto se podría hacer trampa y sin modificar el modelo pero variando la prevalencia de los datos de validación, conseguir mejorar el VPP o el PPN.
¿Cual es entonces la solución? Pues usar métricas que no dependan de la prevalencia. Y esas métricas son la $sensibilidad$ y la $especificidad$ que habíamos descartado. ¿Y para que las queremos? Pues esas 2 métricas nos dicen lo bueno que es nuestro modelo cuando lo estamos desarrollando ya que nos decían cuanto acertaban o fallaban cuando sabíamos lo que debía dar y son métricas independientes de la prevalencia de nuestros datos. Podemos ver que esas métricas no han variado aunque se haya modificado la prevalencia.
Vale, pero nosotros lo que queremos es saber la precisión y la VPN. Pues resulta que el teorema de bayes es una fórmula matemática que nos calcula la precisión y la VPN en base a la sensibilidad y la especificidad y además según la prevalencia. 😍😍😍😍😍😍
$$ P(Enfermo|Positivo)=\frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo|Enfermo)*P(Enfermo)+P(Positivo|Sano)*P(Sano)} $$
$$ P(Sano|Negativo)=\frac{P(Negativo|Sano)*P(Sano)}{P(Negativo|Sano)*P(Sano)+P(Negativo|Enfermo)*P(Enfermo)} $$
y usando los nombres normales de las métricas las fórmulas quedarían así:
$$ Precisión=VPP=\frac{Sensibilidad*Prevalencia}{Sensibilidad*Prevalencia+(1-Especificidad)*(1-Prevalencia)} $$
$$ VPN=\frac{Especificidad*(1-Prevalencia)}{Especificidad*(1-Prevalencia)+(1-sensibilidad)*Prevalencia} $$
Todo ellos nos lleva a que al desarrollar nuestra red neuronal solo nos interesan que los valores de $Sensibilidad$ y de $Especificidad$ sean lo más altos posibles. Y cuando vayamos a predecir, nos tendrán que indicar el valor de la prevalencia y en ese caso podremos calcular si ha salid positivo el valor de $Precisión \; (VPP)$ y si ha salido negativo calcularemos el valor de $VPN$.
Por ello en los prospectos de los test de covid, los valores que siempre se calculaban son el de $Sensibilidad$ y de $Especificidad$: sars-cov-2_rapid_antigen_test_es.pdf
¿Y como sabemos el valor de la prevalencia? Pues nos lo tiene que dar el que hace la predicción o sino en el peor de los casos usar la prevalencia que usamos en nuestros datos. Por lo que en ese caso serían los fórmulas originales de precisión y VPN.
En los siguientes 2 artículos vemos investigaciones para calcular la prevalencia del COVID según distintas circunstancias:
Mejores valores de las métricas
Ahora ya sabemos que VPP y VPN son las métricas que nos interesan realmente y que sus valores deben ser lo más cercanas a 1. Pero también sabemos que esas métricas dependen de la Prevalencia (que no depende de lo bueno que sea nuestro modelo ) y de las métricas de Sensibilidad y Especificidad (Que si que dependen de lo bueno que sea nuestro modelo). Así que para obtener los mejores valores del VPP y VPN tenemos que conseguir en nuestro modelo consigamos los mejores valores de Sensibilidad y Especificidad.
Como ya hemos visto hay las siguientes relaciones entre métricas:
$$
FNR=1-Sensibilidad
$$
$$
FPR=1-Especificidad
$$
Además de
$$
FDR=1-VPP
$$
$$
FOR=1-VPN
$$
Como esas métricas no son independientes de las anteriores, volvamos ahora a poner la tabla de confusión únicamente con las métricas que nos interesan y además los valores ideales que nos interesarían.
| Predicción | |||||
|---|---|---|---|---|---|
| Positivo (PP) | Negativo (PN) | Métricas | |||
| Realidad | Enfermo (E) | TP | FN | $Sensibilidad=1$ | |
| Sano (S) | FP | TN | $Especificidad=1$ | ||
| Métricas | $VPP=1$ | ||||
| $VPN=1$ | |||||
Y por lo tanto el resto de las métricas nos interesarían que fueran 0 pero al depender de la que hemos mostrado , ni las mediremos.
Resumen
Metricas en Keras
Veamos como calcular en Keras las métricas que necesitamos
Sensibilidad
La sensibilidad en inglés es Sensibility pero también se llama Recall que es como se usa en Keras.
Su uso en Keras es
metrics=[tf.keras.metrics.Recall()] metrics=["Recall"]
y usarla como
history.history['recall'] history.history['val_recall']
Ejemplo:
y_true = np.array([1,1,1,1,1]) y_pred = np.array([0.9, 0.2, 0.3, 0.8,0.6]) metric = tf.keras.metrics.Recall() metric(y_true, y_pred).numpy()
0.6
Más información:
Especificidad
Inexplicablemente esta métrica no existe en keras. Pero la podemos definir con el siguiente código:
def specificity(y_true, y_score):
threshold=0.5
y_pred = tf.cast(tf.greater(y_score, threshold), tf.float32)
true_negatives = tf.logical_and(tf.equal(y_true, 0), tf.equal(y_pred, 0))
num_true_negatives=tf.reduce_sum(tf.cast(true_negatives, tf.float32))
negatives =tf.equal(y_true, 0)
num_negatives= tf.reduce_sum(tf.cast(negatives, tf.float32))
specificity = num_true_negatives / (num_negatives + tf.keras.backend.epsilon())
return specificity
Su uso en Keras es
metrics=[specificity]
y usarla como
history.history['specificity'] history.history['val_specificity']
Ejemplo:
y_true = np.array([0,0,0,0,0]) y_pred = np.array([0.9, 0.7, 0.3, 0.3,0.6]) specificity(y_true, y_pred).numpy()
0.4
Métricas de clasificación con más de 2 posibles valores
Categorical Accuracy
Accuracy nos indica la proporción de aciertos que ha tenido. Es decir el porcentaje (en tanto por uno) de verdaderos positivos y verdaderos negativos
Su uso en keras es:
metrics=[tf.keras.metrics.CategoricalAccuracy()] metrics=["categorical_accuracy"]
y usarla como
history.history['categorical_accuracy'] history.history['val_categorical_accuracy']
Mas información:
Ejercicios
Para mostrar la matriz de confusión se usará la siguiente función que usa de
matplotlib
def plot_matriz_confusion(axes,TP=0,TN=0,FP=0,FN=0,fontsize=15,vpp=None,vpn=None,sensibilidad=None,especificidad=None,f1_score=None,mcc=None,auc=None,prevalencia=None):
success_color=matplotlib.colors.to_rgb('#9EE548')
failure_color=matplotlib.colors.to_rgb("#C32240")
blanco_color=matplotlib.colors.to_rgb("#FFFFFF")
if ((vpp is not None) |
(vpn is not None) |
(sensibilidad is not None) |
(especificidad is not None) |
(prevalencia is not None) |
(f1_score is not None) |
(mcc is not None) |
(auc is not None) ):
show_metrics=True
else:
show_metrics=False
if show_metrics==False:
axes.imshow([[success_color,failure_color],[failure_color,success_color]])
else:
axes.imshow([[success_color,failure_color,blanco_color],[failure_color,success_color,blanco_color],[blanco_color,blanco_color,blanco_color]])
labels = ['Positivo','Negativo']
xaxis = np.arange(len(labels))
axes.set_xticks(xaxis)
axes.set_yticks(xaxis)
axes.set_xticklabels(labels, fontsize=13, color="#003B80")
axes.set_yticklabels(labels, fontsize=13, color="#003B80")
axes.text(0, 0, str(TP)+" TP",ha="center", va="center", color="#0A2102",fontsize=fontsize)
axes.text(0, 1, str(FP)+" FP",ha="center", va="center", color="#FAEAEA",fontsize=fontsize)
axes.text(1, 0, str(FN)+" FN",ha="center", va="center", color="#FAEAEA",fontsize=fontsize)
axes.text(1, 1, str(TN)+" TN",ha="center", va="center", color="#0A2102",fontsize=fontsize)
axes.xaxis.tick_top()
axes.set_xlabel('Predicción', fontsize=fontsize, color="#003B80")
axes.xaxis.set_label_position('top')
axes.set_ylabel('Realidad', fontsize=fontsize, color="#003B80")
if show_metrics==True:
if (vpp is not None):
axes.text(0, 2, f"Precision\n{vpp:.2f}",ha="center", va="center", color="#0A2102",fontsize=fontsize-4)
if (vpn is not None):
axes.text(1, 2, f"VPN\n{vpn:.2f}",ha="center", va="center", color="#0A2102",fontsize=fontsize-4)
if (sensibilidad is not None):
axes.text(2, 0, f"Sensibilidad\n{sensibilidad:.2f}",ha="center", va="center", color="#0A2102",fontsize=fontsize-4)
if (especificidad is not None):
axes.text(2, 1, f"Especificidad\n{especificidad:.2f}",ha="center", va="center", color="#0A2102",fontsize=fontsize-4)
metricas_generales=""
if (prevalencia is not None):
metricas_generales=metricas_generales+f"Prevalencia\n{prevalencia:.2f}\n"
if (f1_score is not None):
metricas_generales=metricas_generales+f"F1-score\n{f1_score:.2f}\n"
if (mcc is not None):
metricas_generales=metricas_generales+f"MCC\n{mcc:.2f}\n"
if (auc is not None):
metricas_generales=metricas_generales+f"AUC\n{auc:.2f}"
axes.text(2, 2, metricas_generales,ha="center", va="center", color="#0A2102",fontsize=fontsize-4)
Ejercicio 1
Si una red neuronal para detectar si una radiografía es de un tórax ha predicho lo siguiente:
- Para 13 radiografías que eran de tórax , en 8 ha dicho que era un tórax y en 5 ha dicho que no lo era.
- Para 7 radiografías que no eran un tórax , en 4 ha dicho que no era un tórax y en 3 ha dicho que lo era.
Indica el nº de:
- Verdaderos Positivos (TP)
- Verdaderos Negativos (TN)
- Falsos Positivos (FP)
- Falsos Negativos (FN)
Dibuja la matriz de confusión
Ejercicio 2.A
Seguimos con la red neuronal que predice si una radiografía es de tórax.
Si para 10 imágenes ha sacado los siguientes resultados:
y_score=np.array([0.27, 0.45, 0.76, 0.55, 0.28, 0.04, 0.34,0.4, 0.66, 0.88, 0.94,0.47,0.2])
Indica para cada valor predicho , si ha predicho que era una imagen de tórax o no.
Ejercicio 2.B
Seguimos con la red neuronal que predice si una radiografía es de tórax.
Si para 10 imágenes ha sacado los siguientes resultados:
y_score=np.array([0.27, 0.45, 0.76, 0.55, 0.28, 0.04, 0.34,0.4, 0.66, 0.88, 0.94,0.47,0.2])
Pero los valores verdaderos son los siguientes:
y_true=np.array([1,0,1,0,0,0,1,0,1,1,1,1,0])
Indica el nº de:
- Verdaderos Positivos (TP)
- Verdaderos Negativos (TN)
- Falsos Positivos (FP)
- Falsos Negativos (FN)
Dibuja la matriz de confusión
Ejercicio 2.C
Siguiendo con los datos anteriores y suponiendo que el umbral es 0.5:
y_true=np.array([1,0,1,0,0,0,1,0,1,1,1,1,0]) y_score=np.array([0.27, 0.45, 0.76, 0.55, 0.28, 0.04, 0.34,0.4, 0.66, 0.88, 0.94,0.47,0.2])
Calcula directamente las siguientes métricas:
- Prevalencia
- Sensibilidad
- Especificidad
- VPP
- VPN
Ejercicio 2.D
Calcula ahora los valores de:
- VPP
- VPN
pero usando el teorema de bayes en base a los valores de:
- Prevalencia
- Sensibilidad
- Especificidad
Ejercicio 2.E
Muestra ahora una gráfica con matplolib en la que se vea como evolucionan los valores de VPP y VPN según la prevalencia.
Esa misma gráfica se puede mostrar en Bayesian Clinical Diagnostic Model
Ejercicio 3.A
Crea una red neuronal con los datos de bread cancer con las siguientes características:
- neuronas por capa:
[30,64,32,16,8,1] - Función de activation:
ELU - Nº de epocas:
20 - Optimizador:
Adamcon tasa de aprendizaje de0,0001
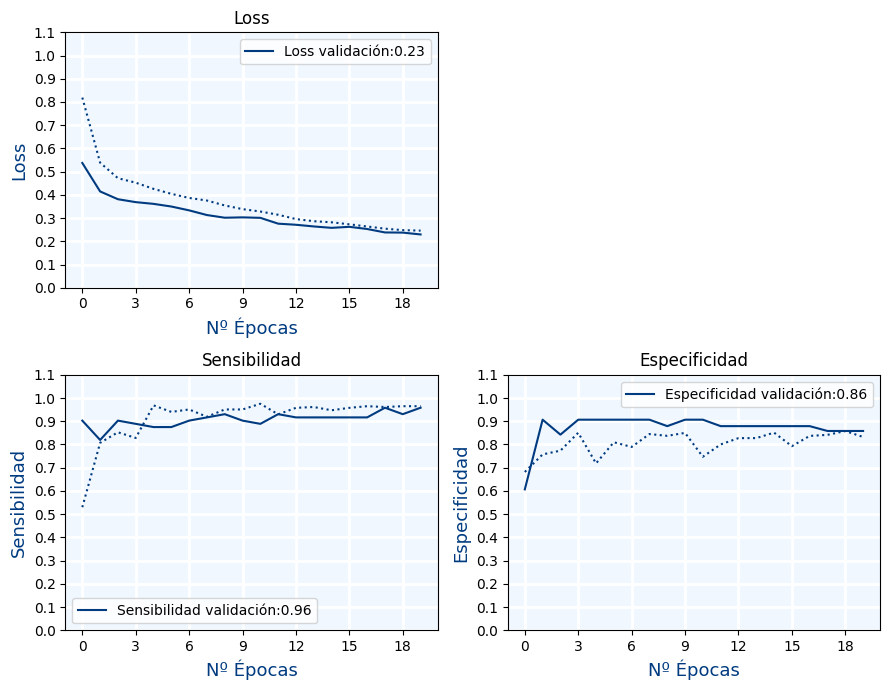
Muestra las siguientes métricas durante el entrenamiento (para cada una de las épocas):
- Loss
- Sensibilidad
- Especificidad
Ejercicio 3.B
En este ejercicio vamos a mostrar la matriz de confusión de la red que acabamos de crear.
Para ello vamos a usar los valores de test que los tenemos en las siguientes variables del ejercicio anterior:
x_testy_test
La variable y_test es lo que llamamos y_true mientras que con x_test obtendremos y_score.
Para ello sigue los siguientes pasos:
- Crea una función llamada
get_matriz_confusion(y_true,y_score,threshold)que retorneTP,TN,FPyFN - Calcula
y_scoreusando el métodopredictdel modelo y usando la variablex_test - Haz que
y_truesea igual ay_test - Llama a la función
get_matriz_confusion - Muestra la matriz de confusión
Ejercicio 3.C
Crea una función llamada get_metrics(TP,TN,FP,FN,Prevalencia=None) que retorne las siguientes métricas:
- Sensibilidad
- Especificidad
- VPP
- VPN
- Prevalencia
Para calcular VPP y VPN se debe usar la prevalencia. Si no se pasa el valor de prevalencia ( Es decir 'prevalencia==None', se usará el de los datos y sino se usará la prevalencia que se pase como argumento.
Usando los valores de TP ,TN, FP y FN del ejercicio anterior, muestra las métricas que retorna get_metrics
Muestra todo en la matriz de confusión.
Ejercicio 3.D
Guarda el modelo a disco
Ejercicio 3.E
En un nuevo jupyter notebook, carga el modelo y con los datos de test , vuelve a mostrar la matriz de confusión con todas las métricas.
Ejercicio 3.F
Muestra ahora 1 gráfica, en la que se mostrará:
- El valor de la sensibilidad y la especificidad según el valor del umbral
¿Que valor de umbral dejarías?
Ejercicio 3.G
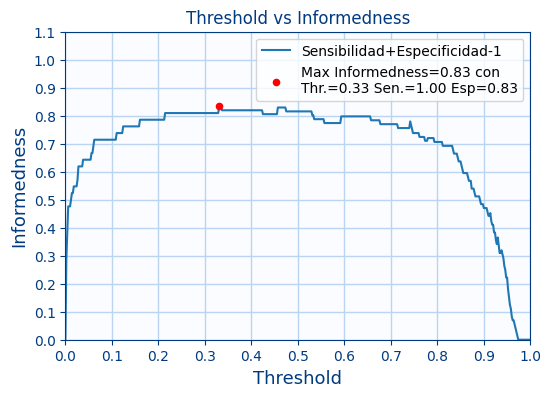
Muestra una gráfica similar a las anteriores pero ahora sea la suma los valores de sensibilidad y la especificidad menos 1.
A la suma de los 2 valores para obtener el máximo pero restando 1 se le llama $Informedness$
$$ Informedness=Sensibilidad+Especificidad-1 $$
Muestra un punto con el máximo de la gráfica y el threshold correspondiente al máximo.Además para ese nivel de threshold, imprime la sensibilidad y la especificidad
Ejercicio 4
Indica en los siguientes problemas si subirías o bajarías el umbral
- Una IA que detecta si hay petroleo en el subsuelo
- Una IA que predice si un usuario en Amazon está cometiendo fraude
- Una IA que decide si te concede un préstamo
- Una IA que decide una persona en un juicio es inocente
- Una IA que corrige automáticamente un examen y te dice si has aprobado
Ejercicio 5.A
Crea una nueva red neuronal para el problema del bread cancer
Ahora razona con cual de las 2 redes te quedarías y que threshold elegirías para cada uno de ellos.
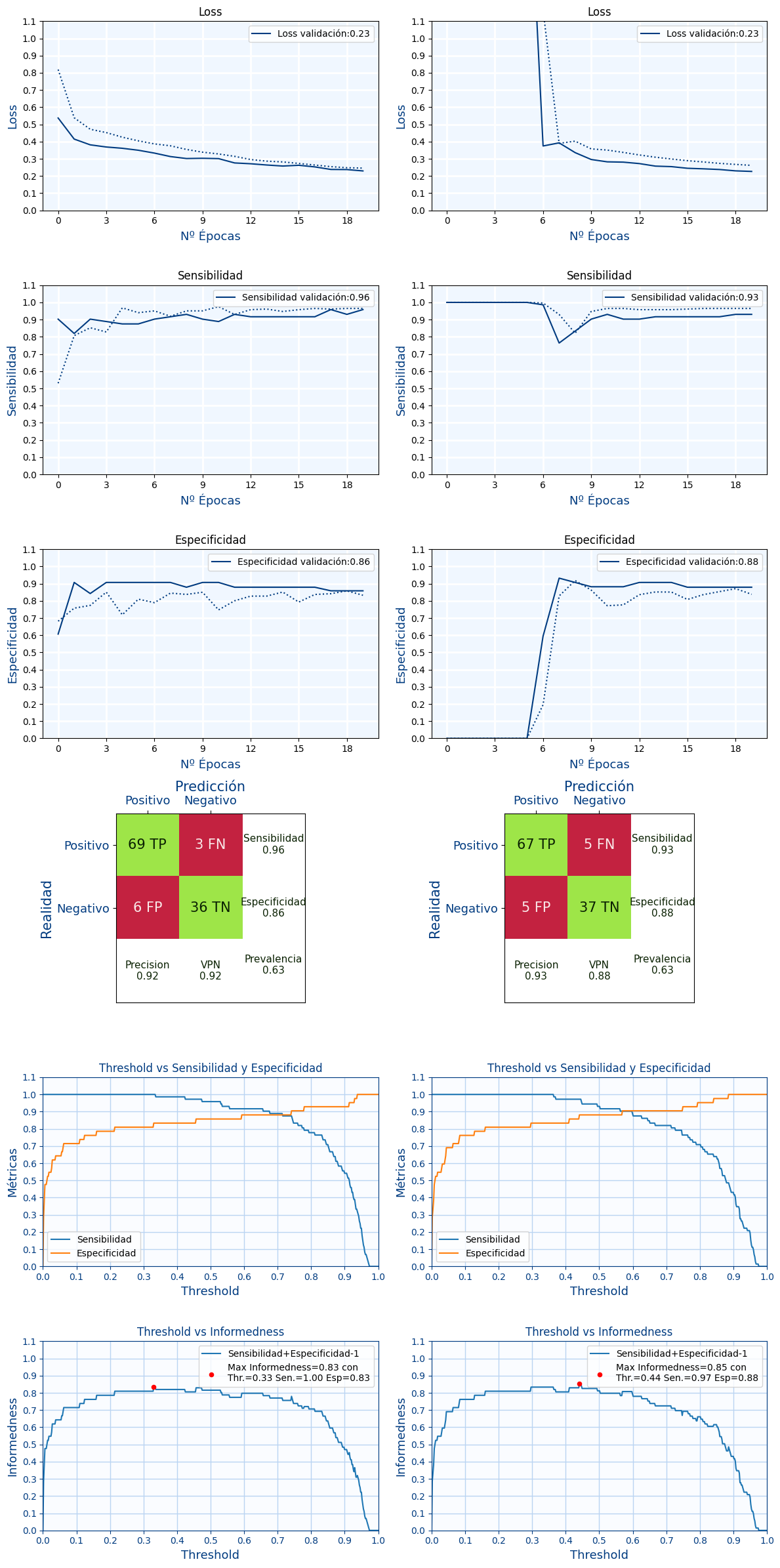
Para elegir debes mostrar gráficas , una al lado de la otra para comparar lo siguiente:
- Gráficos de perdida, sensibilida y especificidad durante el entrenamiento
- Matriz de confusión con las métricas: Sensibilidad, Especificidad, VPP, VPN, Prevalencia
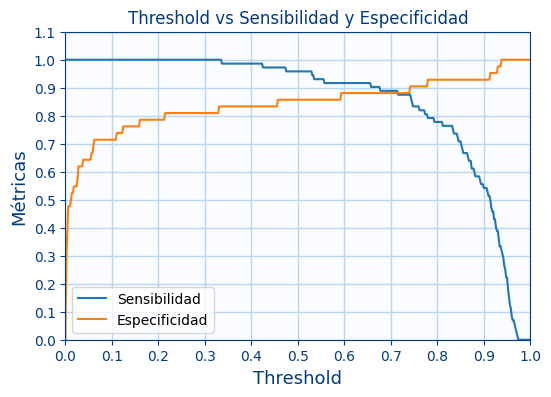
- Threshold vs (Sensibilidad y Especificidad)
- Threshold vs Informedness (Muestra en el label el máximo)
¿Con que red te quedarías?
Además para el nivel de threshold de la red que ha "ganado", imprime la sensibilidad y la especificidad
Ejercicio 5.B
Con el modelo elegido, guarda el modelo a disco
Ejercicio 5.C
Con modelo que has elegido, cárgalo desde disco en otro Jupyter notebook y realiza inferencia de 10 pacientes.
Para cada paciente:
- Indica su prevalencia (te la tienes que inventar de forma aleatoria)
- Indica la probabilidad de que la red haya acertado.
clase/iabd/pia/2eval/tema07.metricas.txt · Última modificación: 2024/10/16 10:03 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3