Herramientas de usuario
Ocultar Menú
−Barra lateral
clase:iabd:pia:2eval:tema07.backpropagation_descenso_gradiente
−Tabla de Contenidos
7.b Descenso de gradiente
El Descenso de gradiente es el algoritmo que usamos para entrenar la red neuronal.
¿Que era entrenar la red neuronal? Pues simplemente pasarle muchos x e y para que obtenga o aprenda los mejores parámetros posibles de pesos (weight) y sesgos (bias) de forma que la función de coste sea mínima.
Sabemos que: y=Salidaverdadera.Laquedeberíahabergeneradolaredneuronal.Sondatosquetenemosrealesdesalida ˆy=Salidapredicha.Laquehageneradolaredneuronal
loss=1NN∑i=1|yi−ˆyi|
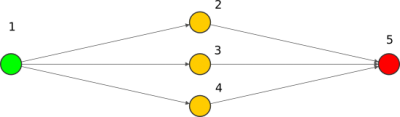
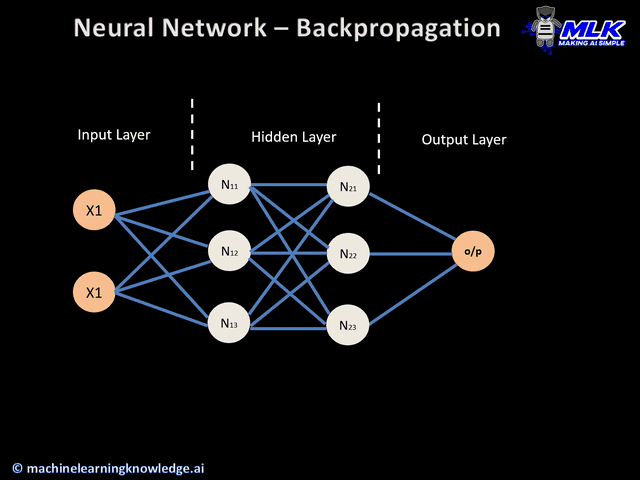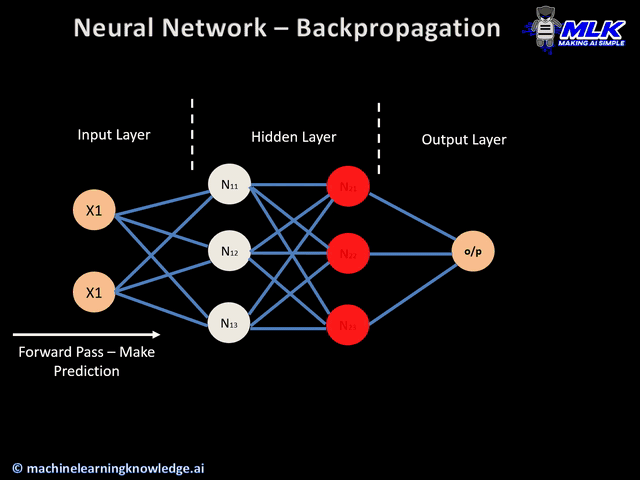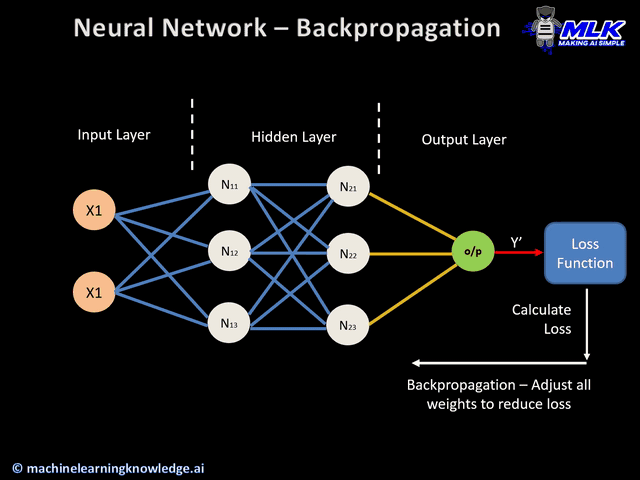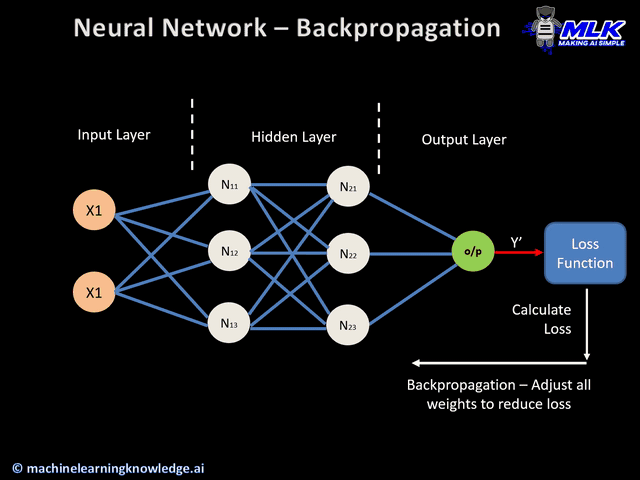
Seguimos con la red neuronal que usamos de ejemplo:
Dedujimos que corresponde a la siguiente fórmula:
ˆy=11+e−(w5,211+e−(w2x+b2)+w5,311+e−(w3x+b3)+w5,411+e−(w4x+b4)+b5)
Ya hemos visto que la siguiente función matemática nos dice los buena que es nuestra red neuronal, al resta el valor real de y la salida de la red neuronal ˆy es decir y−ˆy
loss(x,y,parametros)=1NN∑i=1|yi−11+e−(w5,211+e−(w2xi+b2)+w5,311+e−(w3xi+b3)+w5,411+e−(w4xi+b4)+b5)|
loss(x,y,parametros)=loss(x,y,w2,w3,w4,w5,2,w5,3,w5,4,b4,b2,b3,b5)
Por lo que los parámetros a entrenar son los siguientes: w2,w3,w4,w5,2,w5,3,w5,4,b4,b2,b3,b5.
Es decir que realmente entrenar consiste en averiguar los valores de los parámetros (w2,w3,b2, etc) que hacen que el valor de loss tenga un valor mínimo.
Lo siguiente es saber el algoritmo para averiguar los parámetros. De forma didáctica expongo 3 métodos aunque solo se gasta el último.
- Aleatoriamente: Se podrían elegir aleatoriamente y ver si son bueno y así probar muchas veces hasta encontrar los bueno. Obviamente es una forma malísima ya que la probabilidad de que todos a la vez fueran buenos es extremadamente baja. Por lo que tardaríamos muchísimo tiempo en obtener los parámetros adecuados.
- Todas las combinaciones: Se podrían probar todas las posibles combinaciones, pero hay tantísimas que el coste es prohibitivo y también los hace inviable.
- Descenso de gradiente: El algoritmo consiste en buscar el mínimo de la función ajustando siempre los parámetros un poco de forma que el valor de la función disminuya un poco y repetirlo muchas veces.
Durante este tema la función a minimizar va a ser loss y siguiendo con nuestro ejemplo el código es el siguiente:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def sigmoid(z): return 1/(1 + np.exp(-z))def predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): part1=w_52*sigmoid(w_2*x+b_2) part2=w_53*sigmoid(w_3*x+b_3) part3=w_54*sigmoid(w_4*x+b_4) part4=b_5 z=part1+part2+part3+part4 return sigmoid(z)def loss_mae(y_true,y_pred): error=np.abs(np.subtract(y_true,y_pred)) mean_error=np.sum(error)/len(y_true) return mean_errordef loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): y_pred=predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5) return loss_mae(y_true,y_pred) |
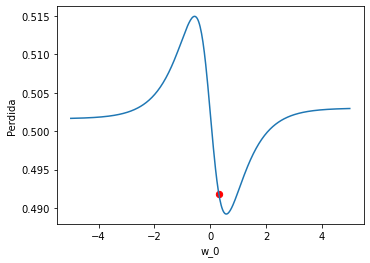
Lo siguiente que vamos a hacer es una gráfica para ver como variaría el valor de loss , es decir la pérdida, en caso de ir variando el valor del peso w_2.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
iris=load_iris()x=iris.data[0:99,2]y_true=iris.target[0:99] model=get_model("mae")w_2_original,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original=get_parameters_from_model(model)perdida=loss(x,y_true,w_2_original,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original)rango_w_2=np.linspace(-5,5,400)perdidas_w_2=[]for w_2 in rango_w_2: perdidas_w_2.append( loss(x,y_true,w_2,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original))figure=plt.figure(figsize=(5.5,4))axes = figure.add_subplot()axes.plot(rango_w_2,perdidas_w_2)axes.scatter(w_2_original,perdida,color="red",s=40)axes.set_xlabel("w_2")axes.set_ylabel('Perdida') |
En la gráfica , el punto rojo es el valor actual de w_2 y la pérdida de la red, es decir el resultado de la función loss.
La curva nos permite ver como evoluciona la pérdida, si vamos variando el valor de w_2.
En nuestro caso, viendo la gráfica podemos encontrar rápidamente el valor de w_2 que haría que fuera mínimo y podríamos darle ese valor
pero debemos tener en cuenta que si variamos mucho w_2 cambiaría totalmente la pérdida para el resto de pesos por lo que hacemos es ir variando poco a poco el valor de cada peso.
En nuestro ejemplo, para hacer que la pérdida sea la mínima, ¿que es mejor que w_2 se haga un poquito más grande o un poquito más pequeño? La respuesta es que lo mejor es que se haga un poquito más grande.
En la siguiente gráfica podemos ver como varia la pérdida para todos los pesos de nuestro ejemplo.
Es decir que como nuestra función de loss tiene muchos parámetros, no podemos encontrar el mínimo de cada parámetro por separado sino que hay que buscar poco a poco el mínimo de cada parámetro.
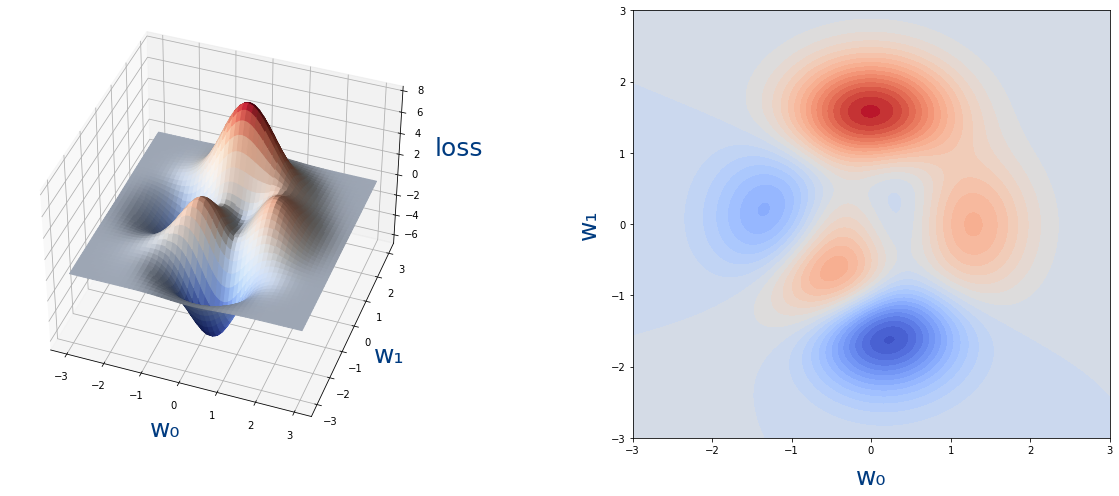
Veamos ahora un ejemplo de una función de loss con dos parámetros:
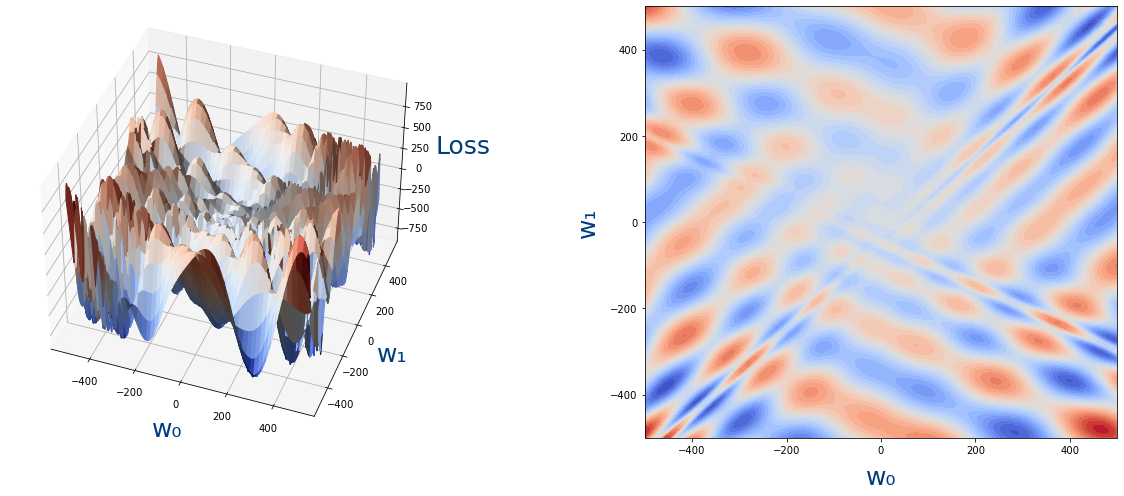
Las dos imágenes son la misma función pero la de la derecha está representada en 2D, donde al "altura" se representa con colores.
Como vemos no podríamos encontrar el mínimo para w_0 y luego para w_1.Así que los haremos poco a poco usando el algoritmo de descenso de gradiente.
Matemáticas en el descenso de gradiente
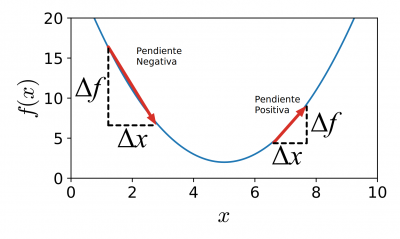
Ahora que vemos la necesidad de encontrar el mínimo de una función pasemos a ver como se encuentra el mínimo. Pues es tan sencillo como imaginarse que estamos en una montaña y para encontrar la parte mas baja solo hay que ir descendiendo por la montaña. Es decir que hay que ver si la función (la montaña) crece y en ese caso ir hacia el lado contrario.
La siguiente imagen ilustra la idea.
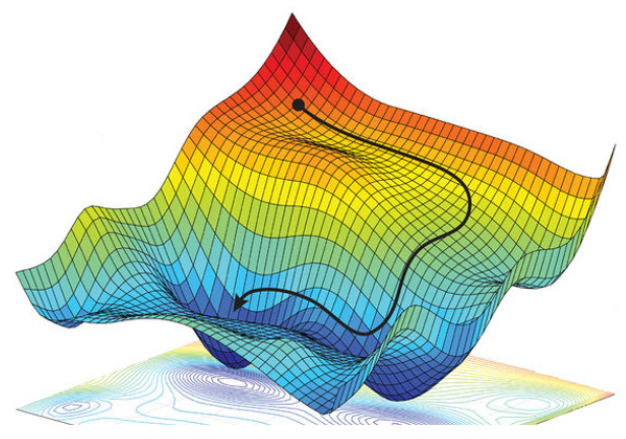
Y podemos jugar con un simulador de descenso de gradiente en Loss Landscape Explorer
Y ver un video de como funciona en LR COASTER | learning rate in machine learning | Loss Landscape visualization | Deep Learning
¿Como hacemos eso matemáticamente? Pues lo primero es pensar que cuando se inicializa la red neuronal, a los parámetros (w0 y w1) se les da un valor aleatorio, por lo que estamos en un punto cualquiera de esa montaña. ¿Como sabemos en que dirección debemos movernos? Pues muy fácil, incrementamos un poquito el valor del parámetro (a ese incremento lo llamaremos h o Δx) y vemos como se incrementa con respecto del valor original, (a ese incremento de la función lo llamamos Δf) . Es decir los restamos (aunque también lo dividimos entre el valor del incremento).
gradientedef(x)=derivadadef(x)=ΔfΔx=limh→0f(x+h)−f(x)h=∂f(x)∂x
Ese valor es lo que se llama la derivada de una función y si:
- Si el resultado de la derivada el positivo, es que la función crece en se punto. Y como estamos buscando el mínimo, deberemos decrementar el valor de x proporcionalmente al valor del gradiente.
- Si el resultado de la derivada el negativo, es que la función decrece en se punto. Y como estamos buscando el mínimo, deberemos incrementar el valor de x proporcionalmente al valor del gradiente.
Una explicación mas detallada de la fórmula se puede ver en el siguiente video: DERIVADAS - Clase Completa: Explicación Desde Cero | El Traductor
En el contexto del descenso de gradiente no se suele hablar que el resultado de la fórmula es la derivada sino el gradiente. Ya que para eso estamos en el descenso de gradente
Para entender la derivada podemos usar estos 2 recursos de Gecebra:
- Pendiente de una recta: La pendiente es el valor de las derivada.
- Cálculo gráfico de derivadas: Se puede ver la derivada (pendiente) en cada punto de una curva
La siguiente fórmula del gradiente queda así con respecto w0 en el punto (w0,w1). La segunda fórmula, es simplemente lo mismo pero expresado de forma mas compacta visto como derivadas.
gradientedew0=limh→0loss(w0+h,w1)−loss(w0,w1)h=∂loss(w0,w1)∂w0
La siguiente fórmula es lo mismo pero para w1
gradientedew1=limh→0loss(w0,w1+h)−loss(w0,w1)h=∂loss(w0,w1)∂w1
Ya sabemos si crece pues en ese caso soy hay que moverse justo para el lado contrario de ahí el "menos" de la siguiente fórmula.
w0=w0−α⋅gradientedew0=w0−α⋅∂loss(w0,w1)∂w0
y
w1=w1−α⋅gradientedew1=w1−α⋅∂loss(w0,w1)∂w1
Si ésto lo repetimos muchas veces es justamente el algoritmo del descenso de gradiente.
La formula general de lo que es el descenso de gradiente se podría expresar así:
wt+1i=wti−α⋅∂loss(wti)∂wti
Expliquemos un poco la fórmula:
- wi es cada uno de los parámetros es decir
w_0,w_1, etc. - El superíndice t el instante de tiempo,ya que vamos a aplicar varias veces la fórmula. Es realmente cada una de las épocas o
epochs. - La variable α es lo que llamamos la tasa de apredizaje o
learning_ratee indica cuanto queremos que varíen los parámetros en cada época.Este valor es muy importante ya que lo que nos dice es "como" de largo vamos a dar los pasos en nuestro descenso de la montaña ya que si damos pasos muy largos en una dirección puede que nos pasemos de largo. En este caso podemos imaginar que podemos ser gigantes que si damos pasos muy largos, nos llegaremos a la parte interior de la montaña. Pero si damos los pasos muy pequeños, no llegaremos a la parte inferior de la montaña antes de acabar las épocas.
Descenso de gradiente en Python
Pasemos ahora a ver como se programa todo ésto en Python.Siguiendo con nuestro ejemplo de:
Ya teníamos el siguiente código:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
import numpy as npimport pandas as pdimport tensorflow as tffrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Densefrom sklearn.datasets import load_iris def get_model(loss,learning_rate): np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() model.add(Dense(3, input_dim=1,activation="sigmoid")) model.add(Dense(1,activation="sigmoid")) model.compile(loss=loss,optimizer=tf.keras.optimizers.SGD(learning_rate=learning_rate)) return modeldef get_w(model,layer,neuron,index): layer=model.layers[layer] return layer.get_weights()[0][index,neuron] def get_b(model,layer,neuron): layer=model.layers[layer] return layer.get_weights()[1][neuron] def get_parameters_from_model(model): w_2 =get_w(model,0,0,0) w_3 =get_w(model,0,1,0) w_4 =get_w(model,0,2,0) w_52=get_w(model,1,0,0) w_53=get_w(model,1,0,1) w_54=get_w(model,1,0,2) b_2 =get_b(model,0,0) b_3 =get_b(model,0,1) b_4 =get_b(model,0,2) b_5 =get_b(model,1,0) return w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5def print_params(cabecera,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): decimals=8 print(cabecera) print("w_2=",round(w_2,decimals)," ","b_2=",round(b_2,decimals)) print("w_3=",round(w_3,decimals)," ","b_3=",round(b_3,decimals)) print("w_4=",round(w_4,decimals)," ","b_4=",round(b_4,decimals)) print("w_52=",round(w_52,decimals)," ","w_53=",round(w_53,decimals),"w_54=",round(w_54,decimals)," ","b_5=",round(b_5,decimals)) def sigmoid(x): return 1/(1 + np.exp(-x)) def predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): part1=w_52*sigmoid(w_2*x+b_2) part2=w_53*sigmoid(w_3*x+b_3) part3=w_54*sigmoid(w_4*x+b_4) part4=b_5 z=part1+part2+part3+part4 return sigmoid(z)def loss_mae(y_true,y_pred): error=np.abs(np.subtract(y_true,y_pred)) mean_error=np.sum(error)/len(y_true) return mean_errordef loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): y_pred=predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5) return loss_mae(y_true,y_pred) |
y ahora añadimos el código de los métodos descenso_gradiente y fit.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
def descenso_gradiente(x,y_true,learning_rate,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): h=0.000003 gradiente_w_2 =(loss(x,y_true,w_2+h,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_w_3 =(loss(x,y_true,w_2,w_3+h,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_w_4 =(loss(x,y_true,w_2,w_3,w_4+h,w_52,w_53,w_54,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_w_52=(loss(x,y_true,w_2,w_3,w_4,w_52+h,w_53,w_54,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_w_53=(loss(x,y_true,w_2,w_3,w_4,w_52,w_53+h,w_54,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_w_54=(loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54+h,b_2,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_b_2 =(loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2+h,b_3,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_b_3 =(loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3+h,b_4,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_b_4 =(loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4+h,b_5)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h gradiente_b_5 =(loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5+h)-loss(x,y_true,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5))/h w_2 =w_2 -learning_rate*gradiente_w_2 w_3 =w_3 -learning_rate*gradiente_w_3 w_4 =w_4 -learning_rate*gradiente_w_4 w_52=w_52-learning_rate*gradiente_w_52 w_53=w_53-learning_rate*gradiente_w_53 w_54=w_54-learning_rate*gradiente_w_54 b_2 =b_2 -learning_rate*gradiente_b_2 b_3 =b_3 -learning_rate*gradiente_b_3 b_4 =b_4 -learning_rate*gradiente_b_4 b_5 =b_5 -learning_rate*gradiente_b_5 return w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5def fit(x, y_true,epochs,learning_rate,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): for epoch in range(epochs): w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5=descenso_gradiente(x,y_true,learning_rate,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5) return w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5 |
Por último usamos todo el código para ver si entrena igual con nuestro código que en Keras.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
learning_rate=0.001epochs=50iris=load_iris()x=iris.data[0:99,2]y_true=iris.target[0:99]model=get_model('mae',learning_rate)w_2_original,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original=get_parameters_from_model(model)print_params("Valor de los pesos antes del entrenamiento:",w_2_original,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original)history=model.fit(x, y_true,epochs=epochs,verbose=False,batch_size=len(x),shuffle=False)w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5=get_parameters_from_model(model)print_params("Valor de los pesos tras entrenamiento usando Keras:",w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5)w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5=fit(x,y_true,epochs,learning_rate,w_2_original,w_3_original,w_4_original,w_52_original,w_53_original,w_54_original,b_2_original,b_3_original,b_4_original,b_5_original)print_params("Valor de los pesos tras entrenamiento Manualmente:",w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Valor de los pesos antes del entrenamiento:w_2= 0.30959857 b_2= 0.0w_3= 0.07310068 b_3= 0.0w_4= 0.63308823 b_4= 0.0w_52= 0.49408045 w_53= -1.1185157 w_54= 0.14808941 b_5= 0.0Valor de los pesos tras entrenamiento usando Keras:w_2= 0.31066534 b_2= -0.00022871w_3= 0.06847349 b_3= 6.122e-05w_4= 0.6330435 b_4= -0.00013335w_52= 0.49511436 w_53= -1.1182635 w_54= 0.14937088 b_5= -9.583e-05Valor de los pesos tras entrenamiento Manualmente:w_2= 0.31066538 b_2= -0.00022871w_3= 0.06847351 b_3= 6.122e-05w_4= 0.63304377 b_4= -0.00013335w_52= 0.49511434 w_53= -1.11826369 w_54= 0.14937088 b_5= -9.583e-05 |
Mas información:
Entrenamiento en Keras
Ya hemos visto como el método fit de Keras realiza el entrenamiento pero veamos un poco más en detalle lo que hay que hacer.
Para el entrenamiento debemos establecer parámetros tanto en fit como en compile. Veamos un ejemplo.
1 2 |
model.compile(loss=loss,optimizer=tf.keras.optimizers.SGD(learning_rate=learning_rate))model.fit(x, y_true,epochs=epochs,verbose=False,batch_size=len(x),shuffle=False) |
compileloss: Ya vimos en el tema anterior que es la fórmula que se usa para calcular la pérdida o coste de la red neuronaloptimizer: Indica el algoritmo de descenso de gradiente que vamos a usar junto con la tasa de aprendizaje olearning_rate. Más adelante en este tema vamos a ver que hay variaciones del algoritmo del descenso de gradiente.
fitepochs: Indicamos cuantas veces se va a aplicar el algoritmo del descenso de gradiente.batch_size: En este tema aun no vamos a ver el significado de este parámetro pero simplemente decir que lo hemos incluido para que el resultado fuera el mismo que con Python.shuffle: Este parámetro no se suele usar y solo lo hemos incluido para que el resultado fuera el mismo que con Python.
Cuando entrenamos por defecto fit nos muestra el resultado del entrenamiento de cada época, indicando el valor de loss en cada una de ellas.
Epoch 1/50 1/1 [==============================] - 0s 282ms/step - loss: 0.4918 Epoch 2/50 1/1 [==============================] - 0s 7ms/step - loss: 0.4917 Epoch 3/50 1/1 [==============================] - 0s 5ms/step - loss: 0.4917 ... ... ... Epoch 48/50 1/1 [==============================] - 0s 3ms/step - loss: 0.4913 Epoch 49/50 1/1 [==============================] - 0s 4ms/step - loss: 0.4913 Epoch 50/50 1/1 [==============================] - 0s 4ms/step - loss: 0.4913
Tanto el método fit como compile tienen muchos más parámetros pero aquí hemos visto únicamente los básicos.
Mas información:
Profundizando en el descenso de gradiente
Vamos ahora a ver de una forma más gráfica como funciona el descenso de gradiente y algunos problemas que tiene.
En este apartado a modo de ejemplo, vamos a usar como función de coste:
loss(w0,w1)=3(1−w0)2e−w20−(w1+1)2−10(w05−w30−w51)e−w20−w21−13e−(w0+1)2−w21
y en Python:
1 2 |
def loss_function(w_0,w_1): return 3*(1 - w_0)**2 * np.exp(-w_0**2 - (w_1 + 1)**2) - 10*(w_0/5 - w_0**3 - w_1**5)*np.exp(-w_0**2 - w_1**2) - 1./3*np.exp(-(w_0 + 1)**2 - w_1**2) |
En los apéndices de este tema está el código que vamos a usar que se usa así:
1 2 3 4 5 6 7 8 9 |
figure=plt.figure(figsize=(16,15))axes = figure.add_subplot()plot_loss_function(axes)epochs=5learning_rate=0.03w_0_original=-0.35w_1_original=-0.67plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(epochs,learning_rate,w_0_original,w_1_original)) |
La función get_puntos_descenso_gradiente tiene los siguientes parámetros:
epochs: El nº de épocas a aplicarlearning_rate: La tasa de aprendizaje a aplicar.w_0_original: El peso inicial dew_0w_1_original: El peso inicial dew_1
Que genera la siguiente gráfica
- La estrella roja es desde donde empieza el algoritmo.Es decir, el valor inicial de los parámetros w0,w1
- La estrella azul es donde acaba el algoritmo.Es decir, el valor tras el entrenamiento de los parámetros w0,w1
- Los puntos amarillo son los pasos por lo que se va moviendo el algoritmo. Cada uno de los valores intermedios de los parámetros durante el entrenamiento.
Optimizadores de Keras
Podemos mejorar nuestro código en Python haciendo que podamos usar directamente los Optimizers de Keras y de esa forma ver como funciona cada uno de ellos. Para poder usarlos directamente vamos a creas las nuevas funciones loss_tf y get_puntos_descenso_gradiente_optimizer adecuadas a TensorFlow y Keras.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def loss_tf(w_0,w_1): return 3*(1 - w_0)**2 * tf.exp(-w_0**2 - (w_1 + 1)**2) - 10*(w_0/5 - w_0**3 - w_1**5)*tf.exp(-w_0**2 - w_1**2) - 1./3*tf.exp(-(w_0 + 1)**2 - w_1**2) def get_puntos_descenso_gradiente_optimizer(epochs,optimizer_function,w_0_init,w_1_init): puntos_descenso_gradiente=np.array([[w_0_init,w_1_init]]) w_0=w_0_init w_1=w_1_init for epoch in range(epochs): var_w_0=tf.Variable(w_0) var_w_1=tf.Variable(w_1) optimizer_function.minimize(lambda: loss_tf(var_w_0,w_1), var_list=[var_w_0]) optimizer_function.minimize(lambda: loss_tf(w_0,var_w_1), var_list=[var_w_1]) w_0=var_w_0.numpy() w_1=var_w_1.numpy() puntos_descenso_gradiente=np.append(puntos_descenso_gradiente,[[w_0,w_1]], axis=0) return puntos_descenso_gradiente |
Lo que ha cambiado principalmente es la función get_puntos_descenso_gradiente_optimizer no hace cálculo del gradiente (derivada) ni actualiza los parámetros, sino que llama a la función de Keras de optimización.
Si usamos get_puntos_descenso_gradiente_optimizer ahora con tf.keras.optimizers.SGD
1 |
get_puntos_descenso_gradiente_optimizer(5,tf.keras.optimizers.SGD(learning_rate=0.03),-0.35,-0.67) |
array([[-0.35 , -0.67 ],
[-0.269319 , -0.72470832],
[-0.13292952, -0.83883744],
[ 0.06544246, -1.06462073],
[ 0.24086528, -1.40752137],
[ 0.26578248, -1.59573841]])
Vamos que el resultado es prácticamente el mismo que cuando lo hicimos manualmente.
Y podemos generar de la misma forma el gráfico:
1 2 3 4 5 |
figure=plt.figure(figsize=(16,15))axes = figure.add_subplot()plot_loss_function(axes)plot_descenso_gradiente(axes,get_puntos_descenso_gradiente_optimizer(5,tf.keras.optimizers.SGD(learning_rate=0.03),-0.35,-0.67)) |
Y obviamente el resultado es el mismo
Learning rate y epochs
Veamos ahora como influye el learning_rate en el funcionamiento del algoritmo de gradiente.
Comparemos la gráfica anterior con un learning_rate de 0.03 con este otro ejemplo con learning_rate de 0.07
1 |
plot_descenso_gradiente(get_puntos_descenso_gradiente(5,0.07,-0.35,-0.67)) |
Podemos ver que ahora que damos pasos demasiado largos y no llegamos hasta el mínimo de la función.
Sigamos con otro ejemplo:
1 |
plot_descenso_gradiente(get_puntos_descenso_gradiente(11,0.1,-0.35,-0.67)) |
El valor de learning_rate es mayor aun , siendo de 0.1 por lo que damos pasos tan grandes que nos salimos de mínimo de la función y eso que hemos pasado de 5 épocas a 11 épocas.
Es decir, si el learning_rate es elevado, no llegará al mínimo aunque pongamos muchas épocas.
Sigamos con otro ejemplo en el que el learning_rate es pequeño, concretamente de 0.006
1 |
plot_descenso_gradiente(get_puntos_descenso_gradiente(11,0.006,-0.35,-0.67)) |
Vemos que al dar pasos tan pequeños nos quedamos a mitad de camino y eso que también hemos puesto 11 épocas. En este caso para solucionarlo solo habría que aumentar el número de épocas.
Así que en el siguiente ejemplo, vamos a aumentar el número de épocas de 11 a 30.
1 |
plot_descenso_gradiente(get_puntos_descenso_gradiente(30,0.006,-0.35,-0.67)) |
Y ahora ya ha llegado hasta el mínimo.
En general nos interesa valores bajos de
learning_rate y altos de epochs.
Mínimos locales y mínimos globales
Ahora vamos a simular distintos valores iniciales de w0 y w1 es decir, suponiendo que el generador de números aleatorios genera unos valores iniciales distintos. Y vamos a comparar que ocurre con los distintos valores iniciales.
1 2 3 4 |
plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(10, 0.03, 0.3 , 1.3))plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(10, 0.03, -0.35, -0.67))plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(10, 0.03, -0.4 , -0.5 ))plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(10, 0.03, -0.3 , -0.5 )) |
Esta última gráfica es muy interesante. No hay que perder de vista que las estrellas rojas es el valor inicial de los pesos que tenemos en nuestra red neuronal. Es decir , son esos pesos aleatorios con los que de inicializa la red neuronal. Pues lo interesante es que según los valores iniciales aleatorios que elijamos, puede que no lleguemos al mínimo de la función (mínimo global), sino a lo que llamamos un mínimo local.
Se puede ver mejor en esta gráfica:
Es decir que el algoritmo del descenso de gradiente no nos garantiza que encontremos el mínimo global de la función sino solo un mínimo local. Lo que conlleva que quizás no encontramos los mejores valores de los parámetros (weight y bias) para nuestra red neuronal.
Para intentar solventar los problemas del algoritmo del descenso de gradiente existen diversas variaciones del mismo que vamos a ver en el siguiente apartado.
Punto de silla
Al entrenar redes neuronales, existe el concepto de "Punto de silla". Es un punto en el que para cada parámetro estaría en un mínimo o máximo local. Su nombre viene de que parece una silla de montar a caballo.
No debe preocuparnos los puntos de silla ya que al actualizar los parámetros, la "forma" de la función de coste cambiará y lo fácil es que se salga del punto de silla.
Usando optimizadores en Keras
Ya hemos visto como funciona el algoritmo del descenso de gradiente pero resulta que existe muchas variaciones sobre el algoritmo básico. Es lo que en Keras se llaman Optimizers.
Lo que pretenden estos optimizadores es hacer que se llegue lo más rápido posible al mínimo además de evitar mínimos locales, etc. El descenso de gradiente que hemos visto es lo que en Keras se llama Stochastic gradient descent (SGD).
Al igual que pasaba otras veces en Keras, los optimizadores se pueden usar de 2 formas distintas y se usan en el método compile con el argumento optimizer:
- Mediante la clase que retorna la función
1 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=0.03)) |
- Mediante un String
1 |
model.compile(loss="binary_crossentropy",optimizer="sgd") |
Notar que el optimizador se define en el método
compile pero donde se usa es con el método fit.
Tipos de optimizadores en Keras
Veamos ahora los distintos tipos de optimizadores que hay en Keras.
Mas información:
Stochastic gradient descent o SGD
Es el que hemos usado hasta ahora. Se llama "Stochastic gradient descent".
- Tiene además los siguientes parámetros:
momentum: Se usa para que tenga en cuenta valores anteriores del gradiente. Valor adecuado si de desea momentum es de 0.9nesterov: Si valeTruese utiliza el algoritmo de Nesterov para el momentum
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="sgd") |
Mas información:
Adagrad
Es como SGD pero intenta aprender el learning_rate
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adagrad(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="adagrad") |
Más información:
RMSprop
Es como AdraGrad pero aprende el learning_rate.
- Tiene además los siguientes parámetros:
rho: Se usa para ver como se aprende ellearning_ratemomentum: Es la tasa de decaimiento dellearning_rate
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.RMSprop(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="rmsprop") |
Más información:
Adadelta
Es como AdraGrad pero learning_rate la aprende sola.
- Tiene además los siguientes parámetros:
learning_rate: Debería valor 1 o un valor elevado ya que siempre va bajando.rho: Se usa para ver como se aprende ellearning_rate
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adadelta(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="adadelta") |
Más información:
Adam
RMSprop + Momentum
- Tiene además los siguientes parámetros:
amsgrad: Si valeTruese comporta como el algoritmo de AMSGrad que es bastante moderno (2018)
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adam(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="adam") |
Más información:
Adamax
Como Adam pero mas estable a ruido del gradiente
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adamax(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="adamax") |
Más información:
Nadam
Como Adam pero se utiliza el algoritmo de Nesterov para el momentum
- Su uso en Keras:
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Nadam(learning_rate=0.03))model.compile(loss="binary_crossentropy",optimizer="nadam") |
Más información:
En nuestros proyectos, solemos necesitar mostrar por pantalla el optimizador que estamos usando y normalmente pasa ésto:
1 2 |
print(tf.keras.optimizers.Adam(learning_rate=0.001))print(tf.keras.optimizers.Adamax(learning_rate=0.00000001)) |
<keras.optimizer_v2.adam.Adam object at 0x7fc4c0d16b60> <keras.optimizer_v2.adamax.Adamax object at 0x7fc4c1db1810>
Pero hay un truco para que se muestre de forma más amigable, que es sobre escribir la función str de la clase Optimizer:
1 |
tf.keras.optimizers.Optimizer.__str__=lambda self: f'{self._name} lr=' + f'{self.learning_rate.numpy():.10f}'.rstrip('0') |
Y si volvemos a ejecutar de nuevo el código:
1 2 |
print(tf.keras.optimizers.Adam(learning_rate=0.001))print(tf.keras.optimizers.Adamax(learning_rate=0.00000001)) |
Adam lr=0.001 Adamax lr=0.00000001
Elección del optimizador.
Al igual que pasaba con las funciones de activación, según el problema, puede ser mejor uno u otro.
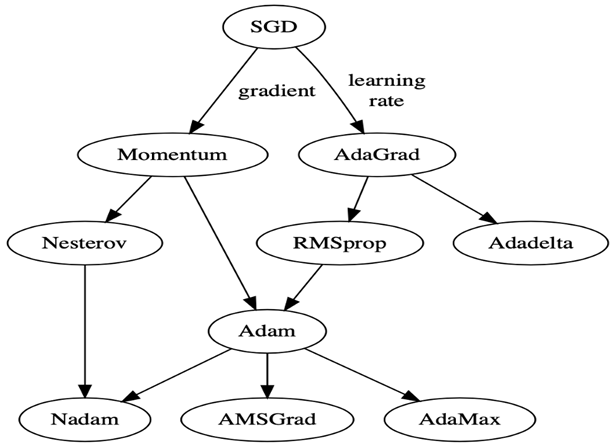
En el siguiente esquema se puede ver la relación entre unos y otros y así ver cual es más moderno.
Usando las funciones que ya tenemos de get_puntos_descenso_gradiente, plot_loss_function, etc. he creado a crear un video para que se vea de la velocidad a la que se mueve cada optimizador.
El objetivo del vídeo no es decir que optimizador es mejor sino hacer ver que hay mejores y peores. En otro problema y con otros parámetros el resultado puede ser distinto.
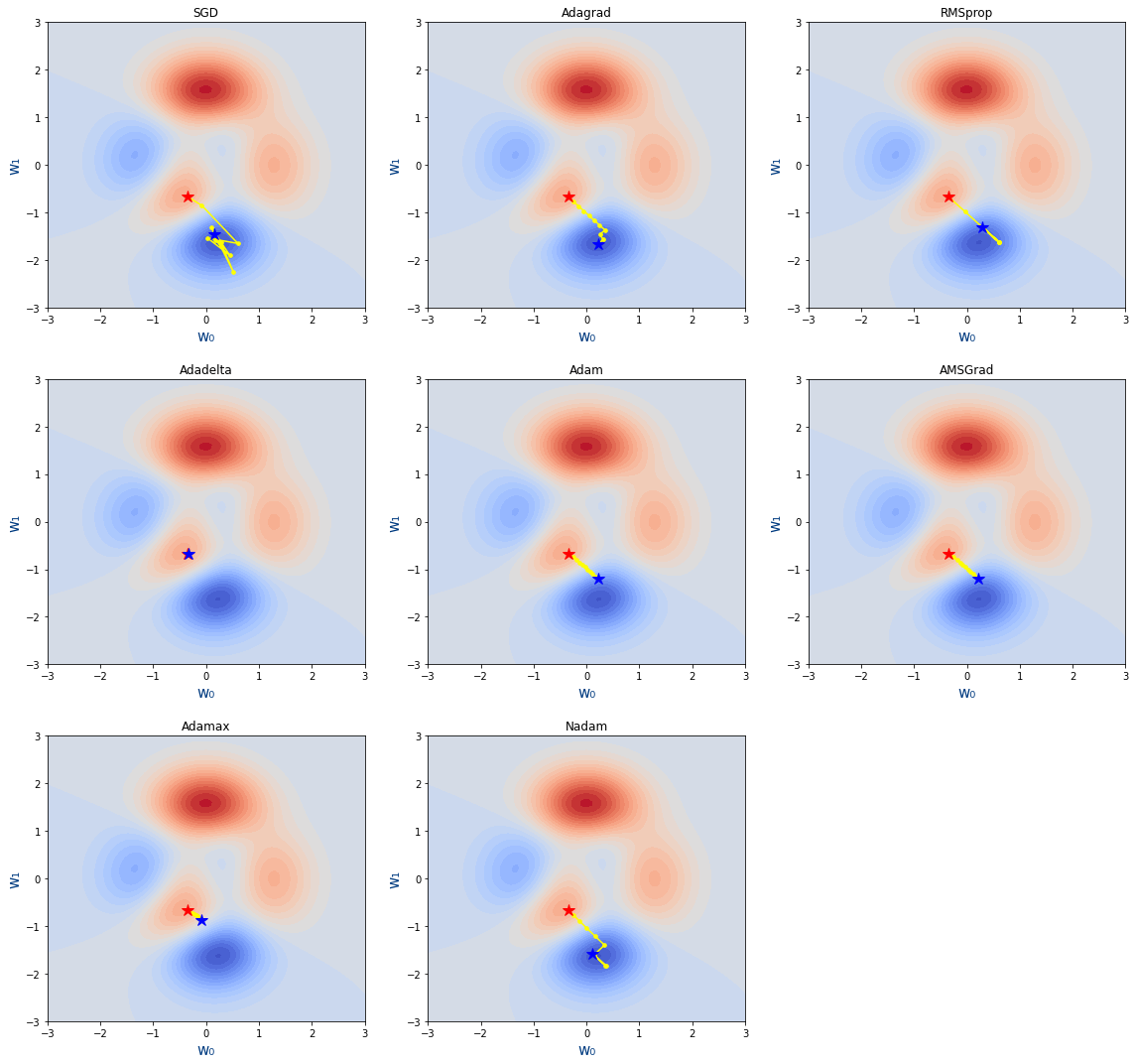
Veamos ahora un ejemplo con código de como funcionan
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
figure=plt.figure(figsize=(16,15))learning_rate=0.1epochs=10optimizers=[ [tf.keras.optimizers.SGD(learning_rate=learning_rate),"SGD"], [tf.keras.optimizers.Adagrad(learning_rate=learning_rate),"Adagrad"], [tf.keras.optimizers.RMSprop(learning_rate=learning_rate),"RMSprop"], [tf.keras.optimizers.Adadelta(learning_rate=1),"Adadelta"], [tf.keras.optimizers.Adam(learning_rate=learning_rate),"Adam"], [tf.keras.optimizers.Adam(learning_rate=learning_rate,amsgrad=True),"AMSGrad"], [tf.keras.optimizers.Adamax(learning_rate=learning_rate),"Adamax"], [tf.keras.optimizers.Nadam(learning_rate=learning_rate),"Nadam"] ]for index,(optimizer,title) in enumerate(optimizers): axes = figure.add_subplot(3,3,index+1) plot_loss_function(axes,15,title) plot_descenso_gradiente(axes,get_puntos_descenso_gradiente_optimizer(epochs,optimizer,-0.35,-0.67)) |
Mas información:
- Dissecting Optimization Algorithms: Contiene gráficas de rendimiento de los distintos algoritmo
- Optimizer: diving deep into Neural Networks: Gráficas buenas.
- Deep study of a not very deep neural network. Part 3b: Choosing an optimizer: Dice que en cada problema hay que elegir un optimizador adecuado.
- Gradient Descent Algorithm — a deep dive: Explicación del descenso de gradiente
- RMSprop saviour of Adagrad: Lo que intenta mejorar RMSprop de Adagrad
- A 2021 Guide to improving CNNs-Optimizers: Adam vs SGD: Las fórmulas de los optimizadores
Backpropagation
El Backpropagation es el algoritmo que optimiza el entrenamiento de la red. Calcular el gradiente (o derivada) de toda la red es muy costoso. Se basa en la idea de que los parámetros de una capa no dependen de la capa anterior.
Si volvemos a ver nuestra red neuronal de ejemplo, podemos calcular los pesos de la neurona 5 sin que influya en como van a ser los pesos de las neuronas 2, 3 y 4. Es decir que empezamos con las neuronas de las capas más hacía la salida y una vez calculados sus pesos , calculamos los parámetros de las capa anterior (más hacia la entrada) , y eso significa ir hacia atrás o backpropagation.
Con backpropagation acabamos de ver el orden en el que se calculan los parámetros de cada neurona y a continuación vamos a ver con el descenso de gradiente como calculamos los parámetros de una neurona.
Junto con el backpropagation aparece otro concepto llamado regla de la cadena o chain rule que se usa para junto al backpropagation para hacer menos cálculos. Está relacionado con el cálculo de derivadas.
En los siguientes videos está explicado perfectamente el backpropagation y la chain rule:
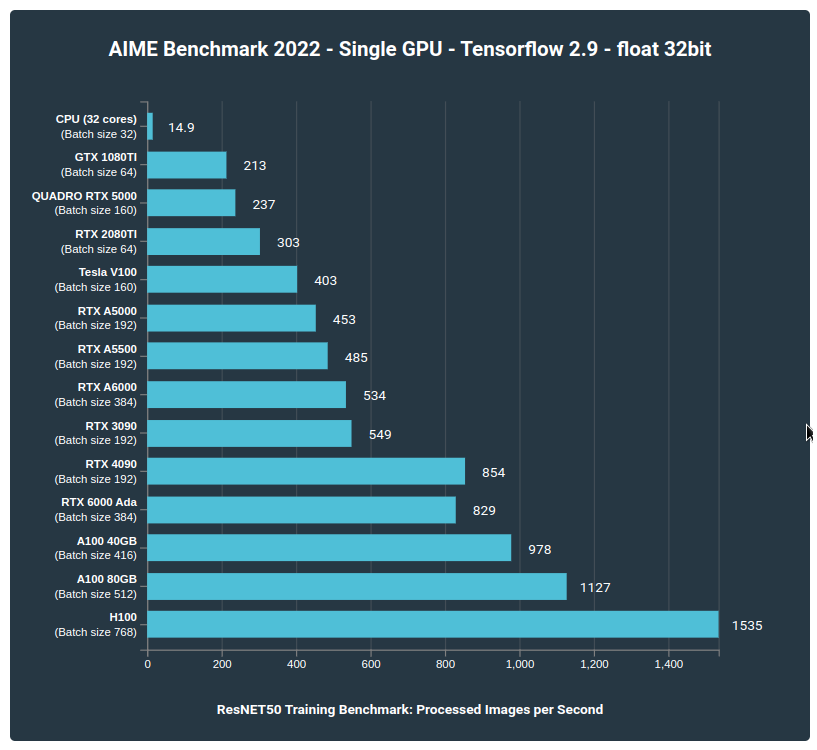
Hardware entrenamiento
Mas información
Ejercicios
Ejercicio 1
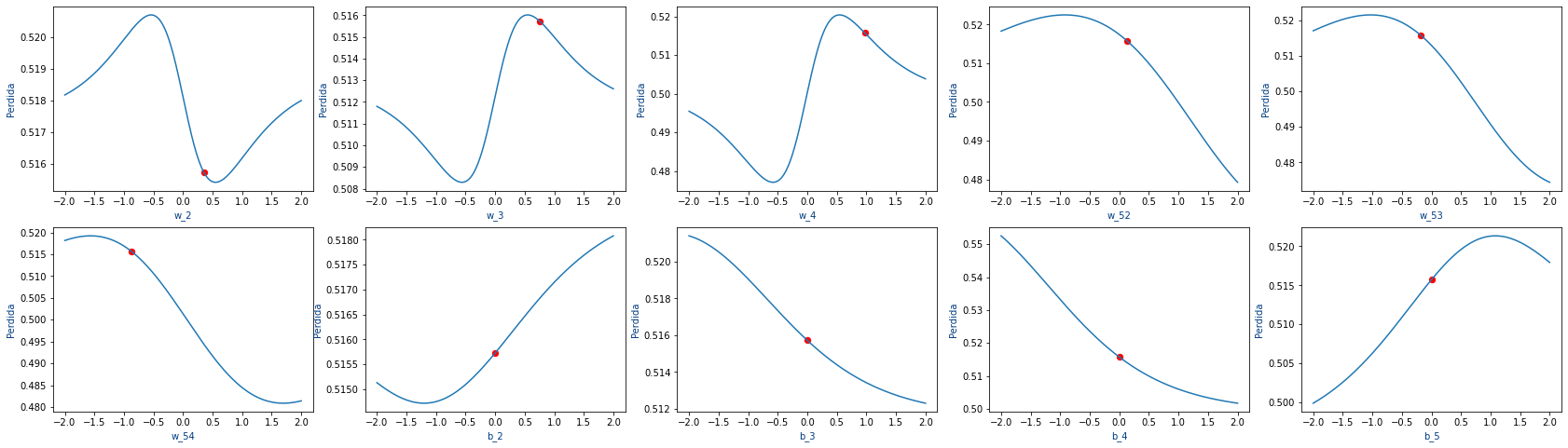
Dado las gráficas de las funciones de coste de una red neuronal:
Indica para cada parámetro: Si la función crece o decrece, el valor de su derivada (positiva o negativa) y por lo tanto si se debe incrementar el valor del parámetro o decremenarlo.
Ejercicio 2
Dado la siguiente función matemática:
f(x)=x1+e−x
- Indica en valor de la función en los puntos -2,-1 y 1
- Indica el valor de la derivada en los puntos anteriores
- Según el valor de la derivada de los puntos anteriores indica si la función crece o decrece y "cuanto"
- Averigua en qué valor la
xtendría el valor mínimo.
Ejercicio 3
Copia el siguiente código python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 |
#Código base de varios ejercicios. import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import load_irisfrom matplotlib.ticker import MaxNLocatorfrom matplotlib.ticker import MultipleLocator def sigmoid(z): return 1/(1 + np.exp(-z)) def predict_formula(x,w,b): return sigmoid(w*x+b) def loss_mae(y_true,y_pred): error=np.abs(np.subtract(y_true,y_pred)) mean_error=np.sum(error)/len(y_true) return mean_error def loss(x,y_true,w,b): y_pred=predict_formula(x,w,b) return loss_mae(y_true,y_pred) def plot_loss(x,y_true,perdida_original,valor_parametro_inicial,rango,perdidas,xlabel,axes): axes.set_ylim(ymin=0.0,ymax=0.7) axes.plot(rango,perdidas) axes.scatter(valor_parametro_inicial,perdida_original,color="#ff0000",s=40) axes.set_xlabel(xlabel) axes.set_ylabel('loss') axes.vlines(x = valor_parametro_inicial, ymin = perdida_original, ymax = 0.7,colors = '#ff0000',linestyle="dashed") axes.text(valor_parametro_inicial+0.1,0.72,f'{xlabel}={valor_parametro_inicial:0.2f}',c="#ff0000") min_x=rango[np.argmin(perdidas)] min_y=np.min(perdidas) axes.vlines(x = min_x, ymin = 0, ymax = min_y,colors = '#00ff00',linestyle="dashed") axes.text(min_x+0.1,0.015,f'{min_x:0.2f}',c="#00ff00") def plot_simple_metrics(axes,history,title): axes.plot(history,linestyle="dotted",label=f"loss :{history[-1]:.2f}",c="#003B80") axes.set_xlabel('Nº Épocas', fontsize=13,color="#003B80") axes.xaxis.set_major_locator(MaxNLocator(integer=True)) axes.set_ylabel('Métricas', fontsize=13,color="#003B80") axes.set_ylim(ymin=0,ymax=1.1) axes.yaxis.set_major_locator(MultipleLocator(0.1)) axes.set_title(title) axes.set_facecolor("#F0F7FF") axes.grid(visible=True, which='major', axis='both',color="#FFFFFF",linewidth=2) axes.legend() def plot_losses(x,y_true,w_inicial,b_inicial,subfigure): perdida_original=loss(x,y_true,w_inicial,b_inicial) kk=subfigure subfigure.suptitle(f'loss={perdida_original:0.2f}',c="#ff0000") axes_w=subfigure.add_subplot(1,2,1) axes_b=subfigure.add_subplot(1,2,2) rango=np.linspace(-5,5,400) perdidas_w=[] perdidas_b=[] for parametro in rango: perdidas_w.append(loss(x,y_true,parametro,b_inicial)) perdidas_b.append(loss(x,y_true,w_inicial,parametro)) plot_loss(x,y_true,perdida_original,w_inicial,rango,perdidas_w,"w",axes_w) plot_loss(x,y_true,perdida_original,b_inicial,rango,perdidas_b,"b",axes_b) return perdida_original def plot_evolucion_parametros(axes,ws,bs): axes.plot(ws,linestyle="solid",label="w",c="#6ABF40") axes.plot(bs,linestyle="solid",label="b",c="#BF9140") axes.set_xlabel('Nº Épocas', fontsize=13,color="#003B80") axes.xaxis.set_major_locator(MaxNLocator(integer=True)) axes.set_ylabel('Valor de los parámetros', fontsize=13,color="#003B80") axes.set_ylim(ymin=-5,ymax=5) axes.yaxis.set_major_locator(MultipleLocator(1)) axes.set_title("Evolución de los parámetros en cada época") axes.set_facecolor("#F0F7FF") axes.grid(visible=True, which='major', axis='both',color="#FFFFFF",linewidth=2) axes.legend() def plot_parametros(x,y_true,parametros): figure=plt.figure(figsize=(8,3.5*(len(parametros)+1)),layout='constrained') figure.suptitle("$y=\\frac{1}{1 + e^{-( w \\cdot x+b )}}$") subfigures = figure.subfigures(nrows=len(parametros)+1, ncols=1) ws=[] bs=[] history=[] for index,(w,b) in enumerate(parametros): subfigure=subfigures[index] loss=plot_losses(x,y_true,w,b,subfigure) ws.append(w) bs.append(b) history.append(loss) axes=subfigures[-1].add_subplot(1,2,1) plot_simple_metrics(axes,history,"loss") axes=subfigures[-1].add_subplot(1,2,2) plot_evolucion_parametros(axes,ws,bs) def descenso_gradiente(x,y_true,learning_rate,w,b): h=0.000003 gradiente_w =(loss(x,y_true,w+h,b)-loss(x,y_true,w,b))/h gradiente_b =(loss(x,y_true,w,b+h)-loss(x,y_true,w,b))/h w=w-learning_rate*gradiente_w b=b-learning_rate*gradiente_b return w,b def plot_descenso_gradiente(x,y_true,w_inicial,b_inicial,learning_rate,epochs): figure=plt.figure(figsize=(8,3.5*epochs),layout='constrained') figure.suptitle("$y=\\frac{1}{1 + e^{-( w \\cdot x+b )}}$") subfigures = figure.subfigures(nrows=epochs+1, ncols=1) w=w_inicial b=b_inicial ws=[] bs=[] history=[] for epoch in range(epochs): if (epochs>1): subfigure=subfigures[epoch] else: subfigure=subfigures loss=plot_losses(x,y_true,w,b,subfigure) ws.append(w) bs.append(b) history.append(loss) w,b=descenso_gradiente(x,y_true,learning_rate,w,b) axes=subfigures[-1].add_subplot(1,2,1) plot_simple_metrics(axes,history,"loss") axes=subfigures[-1].add_subplot(1,2,2) plot_evolucion_parametros(axes,ws,bs) |
Vamos a trabajar con una red neuronal correspondiente a una única neurona y función de activación sigmoide, que corresponde a la siguiente fórmula:
y=11+e−(w⋅x+b)
Lo que debe hacer es entrenar tu manualmente la red , es decir, encontrar los mejores valores de w y b.
Para ello ejecuta el siguiente código:
1 2 3 |
iris=load_iris()x=iris.data[0:99,2]y_true=iris.target[0:99] |
1 2 |
parametros=[(-0.3,0),(0.1,-0.2),(0.4,-0.4),(0.8,-2)]plot_parametros(x,y_true,parametros) |
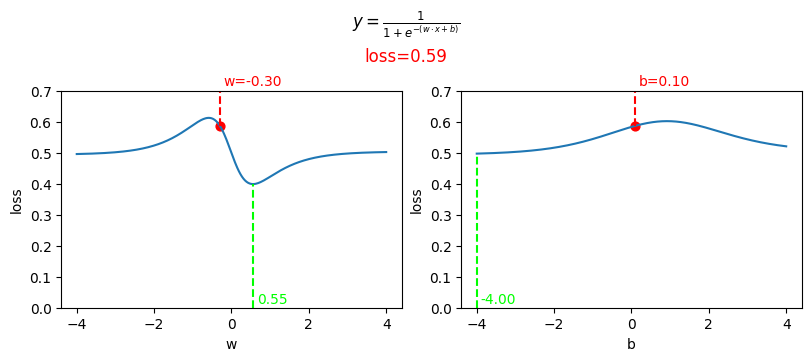
Que muestra la siguiente figura:
Cada par de valores del array parametros son los parámetros en cada una de las épocas.
En las 2 primeras gráficas se muestra en rojo que con los valores de w=-0.3 y b=0 el valor de la pérdida de la red es 0.58. loss=0.50.
Mientras que en verde se muestra los valores que harían mínima cada una de las funciones w=0.56 y b=-5.
Y así sucesivamente con el resto de parámetros
En las últimas gráficas se muestra a la izquierda cada uno de los "loss" que ha habido en cada "época" y a la derecha como han evolucionado los parámetros en cada "época".
Modifica el array parametros añadiendo mas pares de valores de w y b para ver si consigues obtener un valor de loss lo más cercano a 0 que sea posible. Deberás ir modificando poco a poco los valores de w y b.
Ejercicio 4
Entrena ahora la red neuronal usando el descenso de gradiente. Para ello ejecuta el siguiente código:
1 2 3 4 5 6 7 8 9 |
iris=load_iris()x=iris.data[0:99,2]y_true=iris.target[0:99]w_inicial=-0.3b_inicial=0.1learning_rate=0.3epochs=5plot_descenso_gradiente(x,y_true,w_inicial,b_inicial,learning_rate,epochs) |
Modifica los valores de learning_rate y epochs para que la red se entrene sola para obtener un valor de loss lo más cercano a 0 que sea posible.
Ejercicio 5.A
Crea una red neuronal para entrenar las flores. La red tendrá las siguientes características:
- Capas: [4,8,3]
- Función de activación:
selu - Épocas: 400
Y con todas las combinaciones de:
- Optimizadores
- tf.keras.optimizers.SGD
- tf.keras.optimizers.Adagrad
- tf.keras.optimizers.RMSprop
- tf.keras.optimizers.Adam
- tf.keras.optimizers.Adamax
- tf.keras.optimizers.Nadam
- Tasa de aprendizaje
- 0.1
- 0.01
- 0.001
- 0.0001
Muestra las gráficas de la pérdida en función de las épocas de forma que por filas estén los optimizadores y por columnas las tasas de aprendizaje.
Responde las siguientes cuestiones:
- ¿Cual ha resultado ser el mejor optimizador?
- ¿Cual ha sido la mejor tasa de aprendizaje para el mejor optimizador?
- Indica para cada optimizador cual es la mejor tasa de aprendizaje
- Explica que problema tiene en general la tasa de aprendizaje de 0.1
- ¿Que problema tiene en general tasas de aprendizaje altas?
Ejercicio 5.B
Repite el ejercicio anterior pero ahora solo con 20 épocas.
¿Que tasas de aprendizaje y optimizadores se ve que van a generar redes inestables?
Ejercicio 6.A
Haz una red neuronal que averigüe un dígito que se ha escrito a mano. Para ello obtén los datos con el siguiente código:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from sklearn.datasets import load_digitsdef get_datos(): datos=load_digits() x=datos.data y=datos.target label_binarizer = LabelBinarizer() label_binarizer.fit(range(max(y)+1)) y = label_binarizer.transform(y) x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42,stratify=y) return x_train, x_test, y_train, y_test |
La red debería ser realmente una red convolucional pero en este ejemplo usaremos una red neuronal complemente conectada
La red tendrá las siguientes características:
- Neuronas por capa:
64,128,64,32,16,10 - Función de activación de las capas ocultas:
selu
Prueba únicamente con 20 épocas con todas las combinaciones de lo siguiente:
- Optimizadores
- tf.keras.optimizers.SGD
- tf.keras.optimizers.Adagrad
- tf.keras.optimizers.RMSprop
- tf.keras.optimizers.Adam
- tf.keras.optimizers.Adamax
- tf.keras.optimizers.Nadam
- Tasa de aprendizaje
- 0.1
- 0.01
- 0.001
- 0.0005
Muestra las gráficas de la pérdida en función de las épocas de forma que por filas estén los optimizadores y por columnas las tasas de aprendizaje.
Indica para cada tasa de aprendizaje y para cada optimizador si la entrenarías o no y el motivo.
Ejercicio 6.B
Siguiendo con el ejercicio anterior, entrena ahora la red con 300 épocas pero ahora solo con los optimizadores/tasas de aprendizaje que seleccionaste en el ejercicio anterior
Ejercicio 6.C
Repite el ejercicio anterior pero ahora con TODAS las combinaciones de optimizadores y tasas de aprendizaje.
¿Fue adecuada la selección que hiciste en el ejercicio anterior?
clase/iabd/pia/2eval/tema07.backpropagation_descenso_gradiente.txt · Última modificación: 2025/01/22 18:28 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3