Herramientas de usuario
Barra lateral
clase:iabd:pia:2eval:tema07-apendices
Tabla de Contenidos
7. Entrenamiento de redes neuronales e) Apéndices
Tipos de funciones de coste
Huber
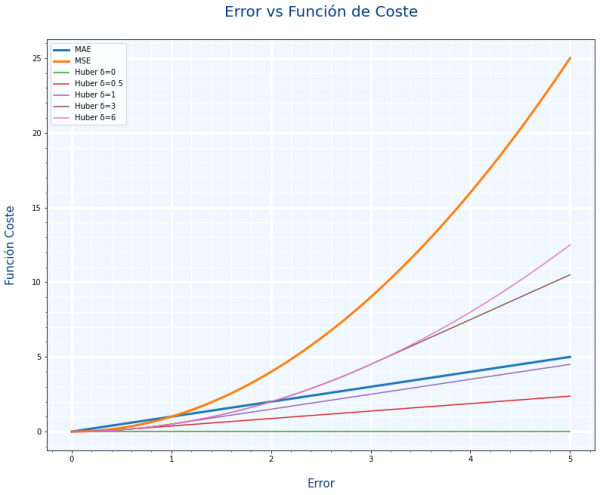
La función de coste Huber es un compromiso entre MAE y MSE, ese compromiso se define con un parámetro llamado delta $\delta$. La siguiente gráfica compara MAE, MSE y distintos valores de delta.
- Si delta tiene en valor cercano a 1, tenderá a parecerse a MAE
- Si delta tiene un valor elevado, tenderá a parecerse a MSE
Como decíamos con MAE y MSE. ¿queremos que los valores extremos se tengan en cuenta. Pues con el parámetro delta podemos hacer un ajuste mas fino
Su uso en Keras es:
model.compile(loss=tf.keras.losses.Huber(delta=3))
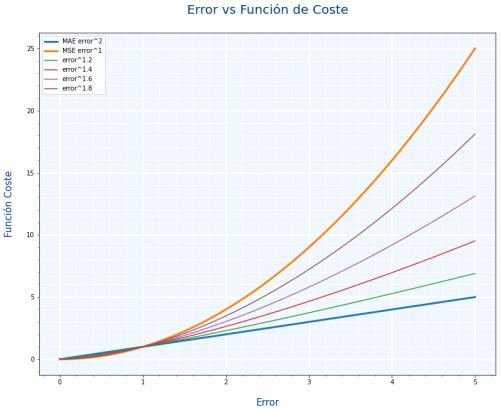
Pensando en la gráfica de Huber he pensado si $MAE=|y-\hat{y}|^1 $ y $MSE=|y-\hat{y}|^2$, en vez de usar Huber, ¿No podríamos usar como función de coste algo también intermedio como $MSE=|y-\hat{y}|^{1.5}$
Y he creado una gráfica similar para ver los resultados y no están mal
He mirado un poco por internet para ver si alguien los usaba y no he encontrado nada, supongo que será porque hacer el cálculo de una potencia con decimales es bastante costoso en tiempo.
Mas información:
Backpropagation
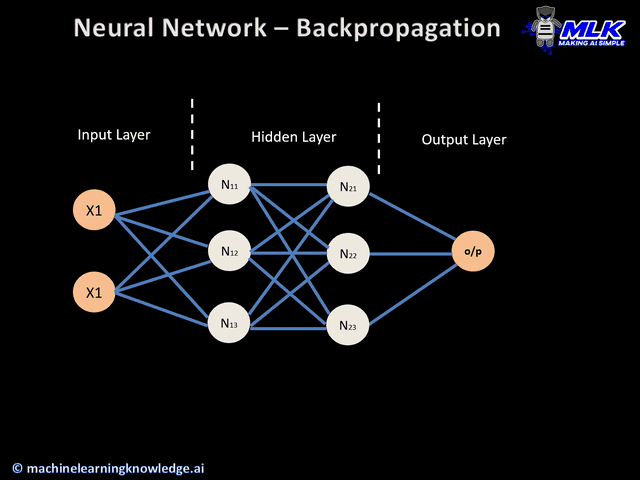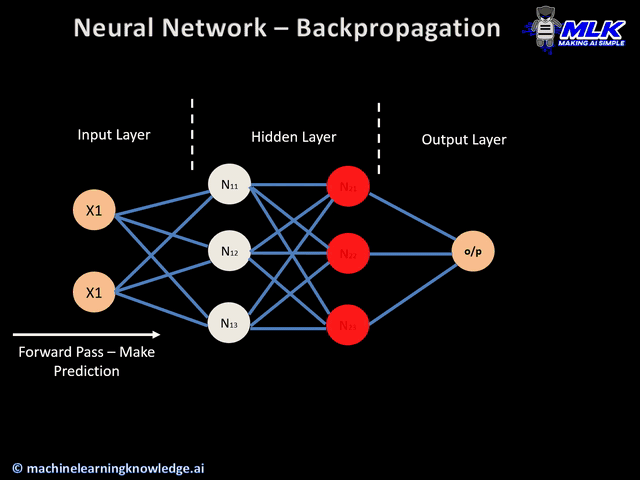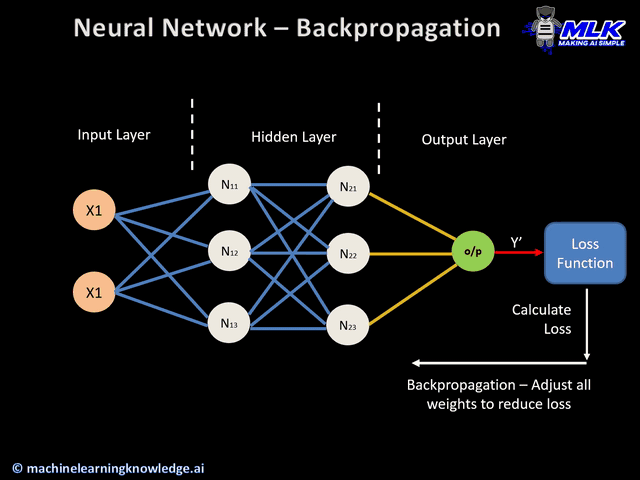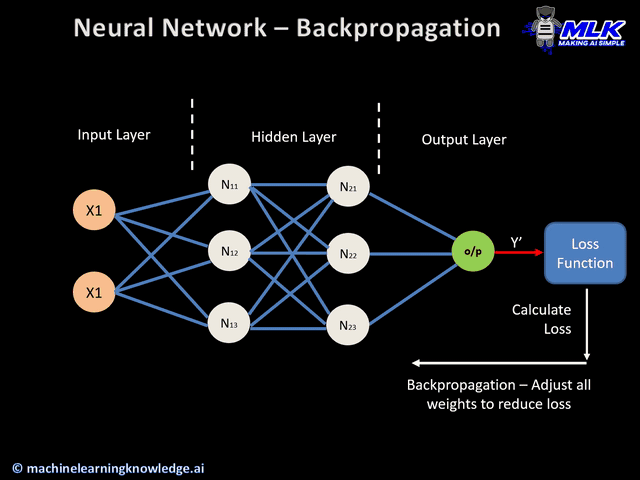
El Backpropagation es el algoritmo que optimiza el entrenamiento de la red. Calcular el gradiente (o derivada) de toda la red es muy costoso. Se basa en la idea de que los parámetros de una capa no dependen de la capa anterior.
Si volvemos a ver nuestra red neuronal de ejemplo, podemos calcular los pesos de la neurona 5 sin que influya en como van a ser los pesos de las neuronas 2, 3 y 4. Es decir que empezamos con las neuronas de las capas más hacía la salida y una vez calculados sus pesos , calculamos los parámetros de las capa anterior (más hacia la entrada) , y eso significa ir hacia atrás o backpropagation.
Con backpropagation acabamos de ver el orden en el que se calculan los parámetros de cada neurona y a continuación vamos a ver con el descenso de gradiente como calculamos los parámetros de una neurona.
Junto con el backpropagation aparece otro concepto llamado regla de la cadena o chain rule que se usa para junto al backpropagation para hacer menos cálculos. Está relacionado con el cálculo de derivadas.
En los siguientes videos está explicado perfectamente el backpropagation y la chain rule:
Creación de los gráficos del descenso de gradiente
Durante el tema hemos visto los gráficos que explican el descenso de gradiente. Veamos ahora como se pueden hacer dichos gráficos en Python.
La función que coste que hemos usado es la siguiente
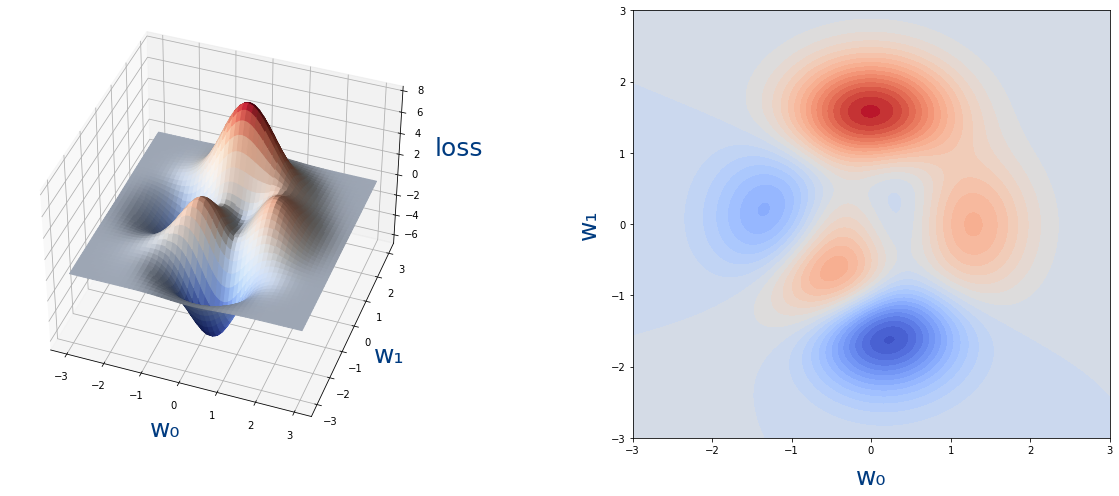
$$ loss(w_0,w_1)=3(1-w_0)^2e^{-w_0^2-(w_1+1)^2}-10(\frac{w_0}{5}-w_0^3-w_1^5)e^{-w_0^2-w_1^2}-\frac{1}{3}e^{-(w_0+1)^2-w_1^2} $$
cuya gráfica es la siguiente:
En python la función $loss(w_0,w_1)$ con NumPy sería así:
def loss(w_0,w_1):
return 3*(1 - w_0)**2 * np.exp(-w_0**2 - (w_1 + 1)**2) - 10*(w_0/5 - w_0**3 - w_1**5)*np.exp(-w_0**2 - w_1**2) - 1./3*np.exp(-(w_0 + 1)**2 - w_1**2)
Y el algoritmo que calcula cada uno de los $w_0,w_1$ del descenso de gradiente es el siguiente:
def get_puntos_descenso_gradiente(epochs,learning_rate,w_0_original,w_1_original):
w_0=w_0_original
w_1=w_1_original
puntos_descenso_gradiente=np.array([[w_0,w_1]])
for epoch in range(epochs):
h=0.00001
gradiente_w_0=(loss(w_0+h,w_1)-loss(w_0,w_1))/h
gradiente_w_1=(loss(w_0,w_1+h)-loss(w_0,w_1))/h
#Nuevos valores de los pesos
w_0=w_0-learning_rate*gradiente_w_0
w_1=w_1-learning_rate*gradiente_w_1
puntos_descenso_gradiente=np.append(puntos_descenso_gradiente,[[w_0,w_1]], axis=0)
return puntos_descenso_gradiente
Si ejecutamos lo siguiente:
get_puntos_descenso_gradiente(5,0.03,-0.35,-0.67)
El resultado es:
array([[-0.35 , -0.67 ],
[-0.26931594, -0.72470447],
[-0.13292324, -0.838827 ],
[ 0.0654496 , -1.06459902],
[ 0.24087009, -1.40749396],
[ 0.2657862 , -1.59573582]])
Que son cada uno de los valores de $w_0,w_1$ que empiezan en -0.35, -0.67 y acaban en 0.2657862, -1.59573582$
Pasamos ahora a mostrar los valores dentro de la gráfica de la función, para ello hemos creado 2 funciones:
plot_loss_function: Que dibuja la superficie con todos los coloresplot_descenso_gradiente: Dibuja los puntos por donde va pasando el algoritmo del descenso de gradiente
def plot_loss_function(axes,fontsize=25,title=""):
rango_w_0=np.linspace(-3,3,100)
rango_w_1=np.linspace(-3,3,100)
rango_w_0,rango_w_1=np.meshgrid(rango_w_0,rango_w_1)
loss=loss_function(rango_w_0,rango_w_1)
axes.contourf(rango_w_0,rango_w_1,loss,30,cmap="coolwarm")
axes.set_xlabel('w₀',fontsize=fontsize,color="#003B80")
axes.set_ylabel('w₁',fontsize=fontsize,color="#003B80")
axes.set_title(title)
def plot_descenso_gradiente(axes,puntos_descenso_gradiente):
axes.scatter(puntos_descenso_gradiente[1:-1,0],puntos_descenso_gradiente[1:-1,1],13,color="yellow")
axes.plot(puntos_descenso_gradiente[:,0],puntos_descenso_gradiente[:,1],color="yellow")
axes.plot(puntos_descenso_gradiente[0,0],puntos_descenso_gradiente[0,1],"*",markersize=12,color="red")
axes.plot(puntos_descenso_gradiente[-1,0],puntos_descenso_gradiente[-1,1],"*",markersize=12,color="blue")
Si ejecutamos el código:
figure=plt.figure(figsize=(16,15)) axes = figure.add_subplot() plot_loss_function(axes) plot_descenso_gradiente(axes,get_puntos_descenso_gradiente(5,0.03,-0.35,-0.67))
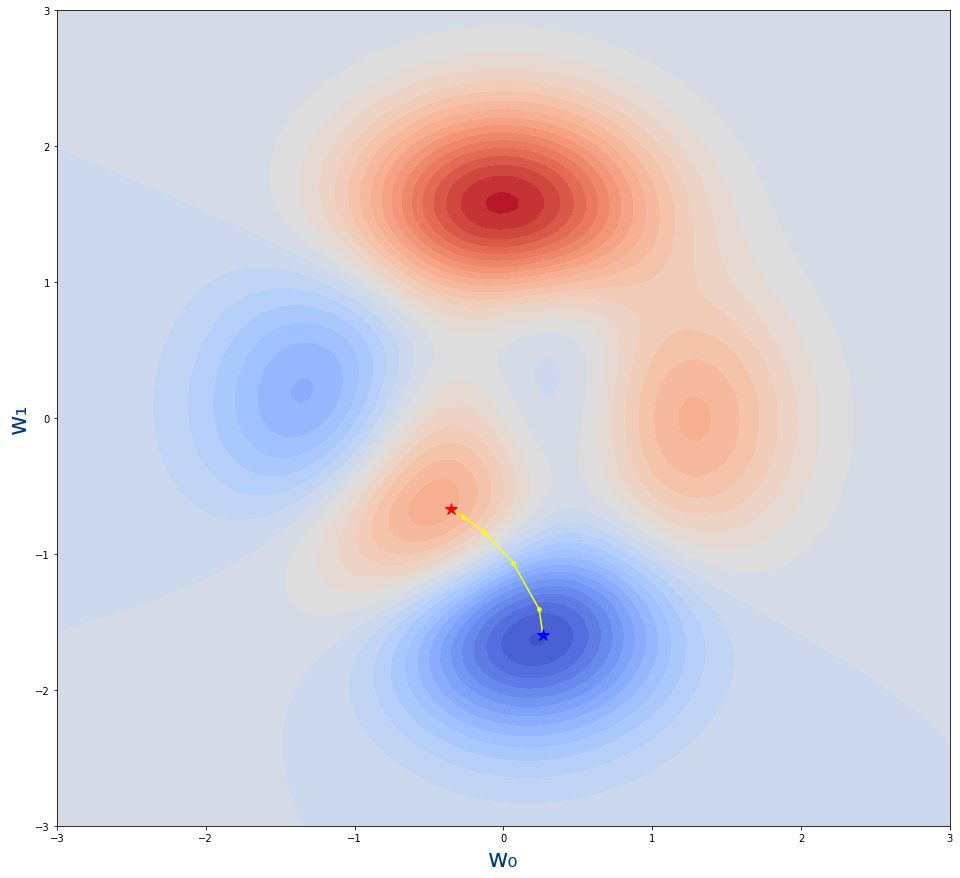
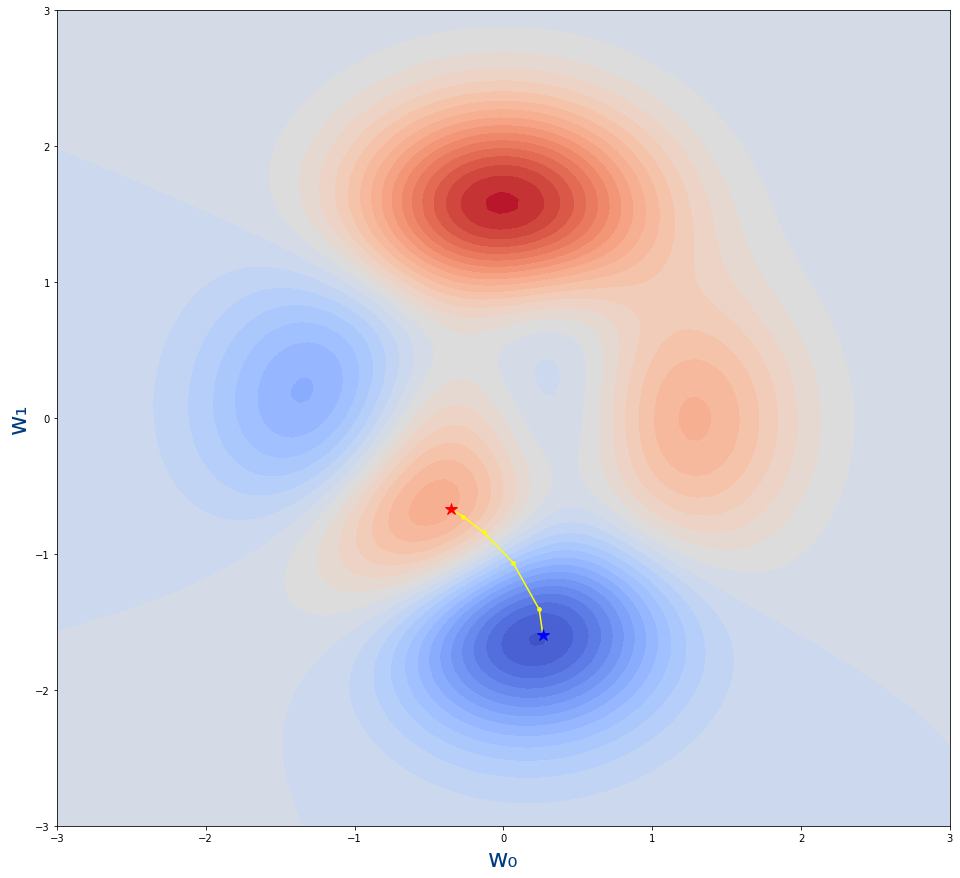
Vemos la siguiente gráfica donde se muestran los puntos que hemos obtenido de la función get_puntos_descenso_gradiente
- La estrella roja es desde donde empieza el algoritmo.Es decir, el valor inicial de los parámetros $w_0,w_1$
- La estrella azul es donde acaba el algoritmo.Es decir, el valor tras el entrenamiento de los parámetros $w_0,w_1$
- Los puntos amarillo son los pasos por lo que se va moviendo el algoritmo. Cada uno de los valores intermedios de los parámetros durante el entrenamiento.
Optimizadores de Keras
Podemos mejorar nuestro código en Python haciendo que podamos usar directamente los Optimizers de Keras y de esa forma ver como funciona cada uno de ellos. Para poder usarlos directamente vamos a creas las nuevas funciones loss_tf y get_puntos_descenso_gradiente_optimizer adecuadas a TensorFlow y Keras.
def loss_tf(w_0,w_1):
return 3*(1 - w_0)**2 * tf.exp(-w_0**2 - (w_1 + 1)**2) - 10*(w_0/5 - w_0**3 - w_1**5)*tf.exp(-w_0**2 - w_1**2) - 1./3*tf.exp(-(w_0 + 1)**2 - w_1**2)
def get_puntos_descenso_gradiente_optimizer(epochs,optimizer_function,w_0_init,w_1_init):
puntos_descenso_gradiente=np.array([[w_0_init,w_1_init]])
w_0=w_0_init
w_1=w_1_init
for epoch in range(epochs):
var_w_0=tf.Variable(w_0)
var_w_1=tf.Variable(w_1)
optimizer_function.minimize(lambda: loss_tf(var_w_0,w_1), var_list=[var_w_0])
optimizer_function.minimize(lambda: loss_tf(w_0,var_w_1), var_list=[var_w_1])
w_0=var_w_0.numpy()
w_1=var_w_1.numpy()
puntos_descenso_gradiente=np.append(puntos_descenso_gradiente,[[w_0,w_1]], axis=0)
return puntos_descenso_gradiente
Lo que ha cambiado principalmente es la función get_puntos_descenso_gradiente_optimizer no hace cálculo del gradiente (derivada) ni actualiza los parámetros, sino que llama a la función de Keras de optimización.
Si usamos get_puntos_descenso_gradiente_optimizer ahora con tf.keras.optimizers.SGD
get_puntos_descenso_gradiente_optimizer(5,tf.keras.optimizers.SGD(learning_rate=0.03),-0.35,-0.67)
array([[-0.35 , -0.67 ],
[-0.269319 , -0.72470832],
[-0.13292952, -0.83883744],
[ 0.06544246, -1.06462073],
[ 0.24086528, -1.40752137],
[ 0.26578248, -1.59573841]])
Vamos que el resultado es prácticamente el mismo que cuando lo hicimos manualmente.
Y podemos generar de la misma forma el gráfico:
figure=plt.figure(figsize=(16,15)) axes = figure.add_subplot() plot_loss_function(axes) plot_descenso_gradiente(axes,get_puntos_descenso_gradiente_optimizer(5,tf.keras.optimizers.SGD(learning_rate=0.03),-0.35,-0.67))
Y obviamente el resultado es el mismo
Métricas
Las métricas que ya las hemos explicado en el tema de métricas son:
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas según el teorema de bayes (PPV,NPV, FDR y FOR)
Las métricas que ahora vamos a ver son métricas que hacen la media entre alguna de las dos métricas que acabamos de indicar.
Para organizar las métricas según 2 criterios:
- Según que métricas juntan
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas (PPV,NPV, FDR y FOR)
- Métricas mixtas, que usa una básica y otra derivada.
- Según la fórmula que usan:
- Media aritmética
- Media armónica
- Media geométrica
- L1-Norma
- L2-Norma
- Ratio
Juntado dos Métricas Básicas
| Fórmula que usan | ||||||
|---|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | L1-Norma | L2-Norma | Ratio |
| Sensibilidad (TPR) y Especificidad (TNR) | $Informedness=TPR+TNR-1$ | |||||
| Sensibilidad (TPR) y FPR | $Positive \; likelihood \; ratio=\frac{TPR}{FPR}$ | |||||
| Especificidad (TNR) y FNR | $Negative \; likelihood \; ratio=\frac{FNR}{TNR}$ | |||||
| FPR y FNR | ||||||
Juntado dos Métricas derivadas
| Fórmula que usan | ||||||
|---|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | L1-Norma | L2-Norma | Ratio |
| PPV y NPV | $Markdness=PPV+NPV-1$ | |||||
| PPV y FOR | ||||||
| NPV y FDR | ||||||
| FDR y FOR | ||||||
Métricas mixtas
Son métricas que juntan una métrica básica con una métrica derivada. Debido a que existen 16 combinaciones no vamos a mostrar todas las que existen, sino solo las que he considerado interesantes.
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | ||||||
|---|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | L1-Norma | L2-Norma | Ratio |
| PPV y Sensibilidad (TPR) | $F_{1}score=\frac{2}{\frac{1}{PPV}+\frac{1}{TPR}}$ | $Fowlkes-Mallows \; index=\sqrt{PPV*TPR}$ | ||||
| NPV y Especificidad (TNR) | ||||||
Más métricas
Indice Jaccard
Este índice es la división entre 2 probabilidades:
$$ Indice \; Jaccard=\frac{P(Positivo \cap Enfermo)}{P(Positivo \cup Enfermo)}=\frac{TP}{TP+FP+FN} $$
- Se deduce de la siguiente forma:
$$ \frac{P(Positivo \cap Enfermo)}{P(Positivo \cup Enfermo)}= $$
$$ \frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo)+P(Enfermo)-P(Positivo \cap Enfermo)}=\frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo)+P(Enfermo)-P(Positivo|Enfermo)*P(Enfermo)} $$
- Sabiendo que:
$$ \begin{array} \\ P(Enfermo)&=&\frac{TP+FN}{TP+FN+FP+TN} \\ P(Sano)&=&\frac{FP+TN}{TP+FN+FP+TN} \\ P(Positivo)&=&\frac{TP+FP}{TP+FN+FP+TN} \\ P(Negativo)&=&\frac{FN+TN}{TP+FN+FP+TN} \\ P(Positivo|Enfermo)&=&\frac{TP}{TP+FN} \end{array} $$
- Entonces:
$$ \frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo)+P(Enfermo)-P(Positivo|Enfermo)*P(Enfermo)}= $$
$$ \left ( \frac{TP}{TP+FN}*\frac{TP+FN}{TP+FN+FP+TN} \right ) \div \left (\frac{TP+FP}{TP+FN+FP+TN}+\frac{TP+FN}{TP+FN+FP+TN}-\frac{TP}{TP+FN}*\frac{TP+FN}{TP+FN+FP+TN} \right )= $$
$$ \left ( \frac{TP}{TP+FN+FP+TN} \right ) \div \left (\frac{TP+FP}{TP+FN+FP+TN}+\frac{TP+FN}{TP+FN+FP+TN}-\frac{TP}{TP+FN+FP+TN} \right )= $$
$$ \left ( \frac{TP}{TP+FN+FP+TN} \right ) \div \left (\frac{TP+FP+TP+FN-TP}{TP+FN+FP+TN} \right )=\left ( \frac{TP}{TP+FN+FP+TN} \right ) \div \left (\frac{TP+FP+FN}{TP+FN+FP+TN} \right )= $$
$$ \frac{TP}{TP+FP+FN}=Indice \; Jaccard $$
- Sin embargo también podemos definir el Indice Jaccard en función de la sensibilidad, la especificidad y la prevalencia.Usando el teorema de bayes podemos definir P(Positivo) de la siguiente forma:
$$ P(Positivo)=\frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Enfermo|Positivo)}= $$
$$ \frac{P(Positivo|Enfermo)*P(Enfermo)}{1} \div \frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo|Enfermo)*P(Enfermo)+P(Positivo|Sano)*P(Sano)}= $$
$$ Sensibilidad*Prevalencia+(1-Especificidad)*(1-Prevalencia) $$
- Y ahora usamos la formula de P(Positivo) en la definición del Indice Jaccard
$$ Indice \; Jaccard=\frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo)+P(Enfermo)-P(Positivo|Enfermo)*P(Enfermo)}= $$
$$ \frac{Sensibilidad*Prevalencia}{Sensibilidad*Prevalencia+(1-Especificidad)*(1-Prevalencia)+Prevalencia-Sensibilidad*Prevalencia}= $$
$$ \frac{Sensibilidad*Prevalencia}{(1-Especificidad)*(1-Prevalencia)+Prevalencia} $$
- Por lo tanto
$$ Indice \; Jaccard=\frac{Sensibilidad*Prevalencia}{(1-Especificidad)*(1-Prevalencia)+Prevalencia} $$
Prevalence threshold
La métrica de Prevalence threshold está explicada en Prevalence threshold (ϕe) and the geometry of screening curves.
Lo único que diremos respecto a la formula es que en el artículo aparece como:
$$ Prevalence \; threshold=\frac{\sqrt{Sensibilidad(1-Especificidad)}+(Especificidad-1)}{Sensibilidad+Especificidad+1} $$ Que jugando un poco con los signos se obtiene la formula equivalente que aparece en Wikipedia: $$ Prevalence \; threshold=\frac{\sqrt{Sensibilidad*FPR}-FPR}{Sensibilidad-FPR} $$
Diagnostic odds ratio
Se define como la división entre Positive likelihood ratio (LR+) y Negative likelihood ratio (LR-)
$$ DOR=\frac{LR+}{LR-}=\frac{TP*TN}{FP*FN} $$
- Aunque también se puede definir en función de la sensibilidad y la especificidad
$$ DOR=\frac{LR+}{LR-}=\frac{\frac{TPR}{1-TNR}}{\frac{1-TPR}{TNR}}=\frac{Sensibilidad*Especificidad}{(1-Sensibilidad)(1-Especificidad)} $$
Matthews Correlation Coefficient o MMC
Es otra métrica pero que tiene en cuenta que los datos no estén balanceados.
El MMC tiene un valor entre -1 a 1. Siendo:
- 1 : El clasificador funciona perfectamente
- 0 : El clasificador acierta aleatoriamente
- -1 : El clasificador acierta peor que aleatoriamente, es decir que clasifica al revés "perfectamente"
$$MCC = \frac{ \mathit{TP} \times \mathit{TN} - \mathit{FP} \times \mathit{FN} } {\sqrt{ (\mathit{TP} + \mathit{FP}) ( \mathit{TP} + \mathit{FN} ) ( \mathit{TN} + \mathit{FP} ) ( \mathit{TN} + \mathit{FN} ) } }$$
Podemos hacer uso de la métrica con la función sklearn.metrics.matthews_corrcoef de sklearn
Ejemplo de uso:
from sklearn.metrics import matthews_corrcoef
y_true = [1,1,1,1,0,0,0,0]
y_pred = [1,1,1,1,0,0,0,0]
print("Valor para una predicción que acierta siempre=",matthews_corrcoef(y_true,y_pred))
y_true = [1,1,1,1,0,0,0,0]
y_pred = [1,1,0,0,1,1,0,0]
print("Valor para una predicción que acierta la mitad=",matthews_corrcoef(y_true,y_pred))
y_true = [1,1,1,1,0,0,0,0]
y_pred = [0,0,0,0,1,1,1,1]
print("Valor para una predicción que nunca acierta=",matthews_corrcoef(y_true,y_pred))
Valor para una predicción que acierta siempre= 1.0 Valor para una predicción que acierta la mitad= 0.0 Valor para una predicción que nunca acierta= -1.0
Mas información:
clase/iabd/pia/2eval/tema07-apendices.txt · Última modificación: 2024/03/19 17:04 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3