Herramientas de usuario
Barra lateral
clase:iabd:pia:2eval:tema07
Tabla de Contenidos
7. Entrenamiento de redes neuronales a) Funciones de coste
Hasta ahora hemos visto como funciona una red neuronal cuando le pasamos los parámetros de entrada y ella calcula la salida. En este tema vamos a ver como se calculan los parámetros de la red neuronal.
Para poder calcular los mejores parámetros de la red neuronal primero debemos saber como es de buena la salida que genera nuestra red neuronal. Para ello vamos a comparar la salida que debería dar la red neuronal con lo que realmente está generando la red neuronal. Así que a partir de ahora a las salida las vamos a diferenciar y llamar de forma distinta
$$y= Salida \: verdadera. \: La \: que \: debería \: haber \: generado \: la \: red \: neuronal. Son \: datos \: que \: tenemos \: reales \: de \: salida$$ $$\hat{y}= Salida \: predicha. \: La \: que \: ha \: generado \: la \: red \: neuronal$$
Por lo tanto la red neuronal debería ser así:
$$y=f(x)$$
pero lo que realmente va a hacer es:
$$\hat{y}=\hat{f}(x)$$
En keras se suele usar la siguiente nomenclatura
y_true = Salida verdadera y_pred = Salida predicha
¿como de buena es nuestra red neuronal? Pues no hay mas que comprar $y$ con $\hat{y}$. Cuanto más se parezcan, mejor será la red.
La forma mas fácil de ver las diferencias que hay entre $y$ e $\hat{y}$ es simplemente restarlas y eso nos dará lo que llamamos el error:
$$error_i=y_i-\hat{y}_i$$
Pero como tenemos muchas $y$ e $\hat{y}$ así que deberemos sumar todos los errores y hacer la media (dividirlo entre el número de datos):
A las funciones de coste también se les llama funciones de pérdida o loss en inglés.
$$loss=error \: medio=\frac{1}{N} \sum_{i=1}^{N} error_i =\frac{1}{N} \sum_{i=1}^{N} (y_i-\hat{y}_i)$$
sin embargo este primer intento no es muy adecuado ya que la suma de los errores positivos mas los errores negativos se podrían cancelar y obtener que no hay coste.
La primera función de coste sería entonces hacer el valor absoluto de los errores.
$$loss \: con \: MAE=error \: medio \: con \: MAE=\frac{1}{N} \sum_{i=1}^{N}|y_i-\hat{y}_i|$$
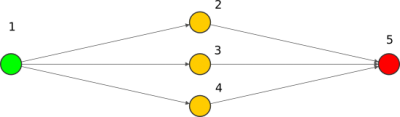
Siguiendo con nuestro ejemplo de:
$$\hat{y}=\frac{1}{1 + e^{-( w_{5,2}\frac{1}{1 + e^{-( w_{2}x+b_{2} )}}+w_{5,3}\frac{1}{1 + e^{-( w_{3}x+b_{3} )}}+w_{5,4}\frac{1}{1 + e^{-( w_{4}x+b_{4} )}}+b_5 )}}$$
Nos queda que el coste es:
$$ \large loss(x,y,parámetros)=\frac{1}{N} \sum_{i=1}^{N}|y_i-\frac{1}{1 + e^{-( w_{5,2}\frac{1}{1 + e^{-( w_{2}x+b_{2} )}}+w_{5,3}\frac{1}{1 + e^{-( w_{3}x+b_{3} )}}+w_{5,4}\frac{1}{1 + e^{-( w_{4}x+b_{4} )}}+b_5 )}}| $$
La formula completa no es importante pero si saber que el error depende tanto de los $parámetros$, de la $x$ y de la $y$ verdadera.
Veamos el código en Python:
Teníamos del tema anterior la creación de la red en Keras y hemos usado como loss (función de pérdida) a MAE:
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.datasets import load_iris
def get_model(loss):
np.random.seed(5)
tf.random.set_seed(5)
random.seed(5)
model=Sequential()
model.add(Dense(3, input_dim=1,activation="sigmoid"))
model.add(Dense(1,activation="sigmoid"))
model.compile(loss=loss)
return model
Ahora creamos la función get_parameters_from_model para obtener los parámetros del modelo.
def get_w(model,layer,neuron,index):
layer=model.layers[layer]
return layer.get_weights()[0][index,neuron]
def get_b(model,layer,neuron):
layer=model.layers[layer]
return layer.get_weights()[1][neuron]
def get_parameters_from_model(model):
w_2 =get_w(model,0,0,0)
w_3 =get_w(model,0,1,0)
w_4 =get_w(model,0,2,0)
w_52=get_w(model,1,0,0)
w_53=get_w(model,1,0,1)
w_54=get_w(model,1,0,2)
b_2 =get_b(model,0,0)
b_3 =get_b(model,0,1)
b_4 =get_b(model,0,2)
b_5 =get_b(model,1,0)
return w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5
La creación de la red neuronal mediante la fórmula es:
def sigmoid(z):
return 1/(1 + np.exp(-z))
def predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5):
part1=w_52*sigmoid(w_2*x+b_2)
part2=w_53*sigmoid(w_3*x+b_3)
part3=w_54*sigmoid(w_4*x+b_4)
part4=b_5
z=part1+part2+part3+part4
return sigmoid(z)
Hasta aquí todo es prácticamente igual que el tema anterior. Ahora pasemos a definir la función de coste de MAE
def loss_mae(y_true,y_pred):
error=np.abs(np.subtract(y_true,y_pred))
mean_error=np.sum(error)/len(y_true)
return mean_error
Y por último vamos a calcular el loss tanto con Keras como con la función de coste:
iris=load_iris()
x=iris.data[0:99,2]
y_true=iris.target[0:99]
model=get_model("mae")
history=model.fit(x, y_true,epochs=1500,verbose=False)
w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5=get_parameters_from_model(model)
y_pred=predict_formula(x,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5)
print("loss con la formula:",loss_mae(y_true,y_pred),sep="\t\t")
print("loss con Keras :",history.history['loss'][-1],sep="\t\t")
loss con la formula: 0.006047901766686328 loss con Keras : 0.006072826683521271
En redes neuronales se suelen usar entre otras las siguientes funciones de coste:
- Problemas de regresión
- Mean Absolute Error (MAE). Error absoluto medio
- Mean Square Error (MSE). Error cuadrático medio
- Huber
- Distancia del coseno.
- Problemas de clasificación:
- Binary Cross Entropy
- Categorical Cross Entropy
Hay mas funciones de coste que se usan en otros problemas como por ejemplo en imágenes pero aquí solo vamos a ver lo básico.
Mas información:
Uso en Keras
Al igual que pasaba con las funciones de activación, las funciones de coste se pueden definir de 3 formas distintas y se usan en el método compile con el argumento loss:
# Mediante un String model.compile(loss='mean_squared_error') # Mediante la función model.compile(loss=tf.keras.losses.mean_squared_error) # Mediante una clase que retorna la función model.compile(loss=tf.keras.losses.MeanSquaredError())
La ventaja de usar la clase es podremos parametrizar la función. Por ejemplo, la función de perdida Huber tiene un parámetro llamado delta $\delta$.
model.compile(loss=tf.keras.losses.Huber(delta=1.2))
Mas información:
Veamos ahora las distintas funciones de coste
MAE
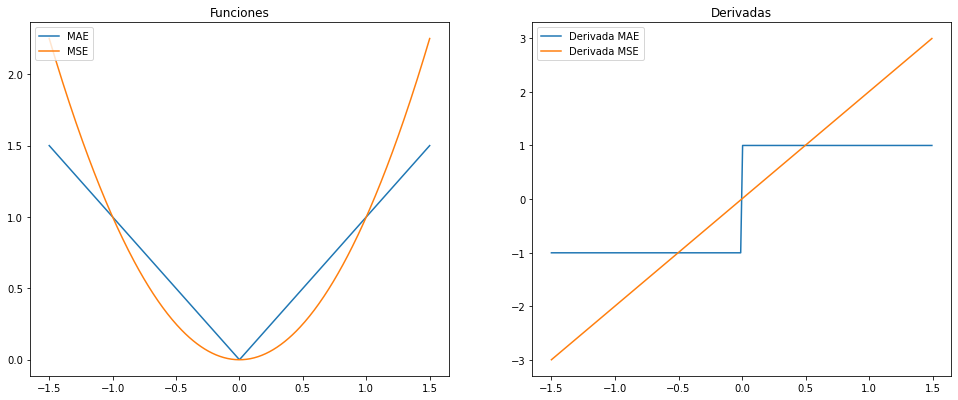
El error absoluto medio o en inglés Mean Absolute Error (MAE) suma el valor absoluto de los errores. Al hacer el valor absoluto de cada error, no se cancelarán si hay errores positivos y negativos.
Su fórmula es:
$$MAE = \frac{1}{N} \sum_{i=1}^{N}|y_{i} - \hat{y_{i}}|$$
Su uso en Keras es:
model.compile(loss="mean_absolute_error") model.compile(loss="mae") model.compile(loss=tf.keras.losses.mean_absolute_error) model.compile(loss=tf.keras.losses.MeanAbsoluteError())
MAE vs MSE
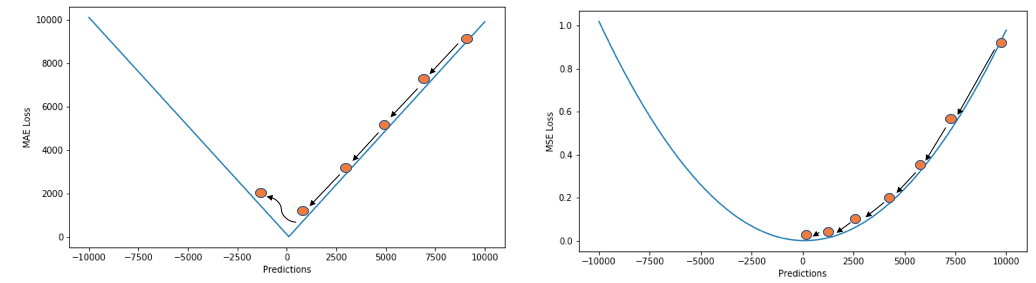
Con el algoritmo de descenso de gradiente nunca nos interesa usar MAE como función de coste ya que el valor de su derivada siempre es constante por lo que al llegar cerca del mínimo es muy fácil que no lo alcance al ser los pasos demasiado largos para llegar al mínimo y pasará sobre él.
Mas información:
Mas información:
MSE
El error cuadrático medio o en inglés Mean Square Error (MSE) es similar al anterior solo que eleva al cuadrado cada uno de los errores.
Su fórmula es:
$$MSE = \frac{1}{N} \sum_{i=1}^{N}|y_{i} - \hat{y_{i}}|^2$$
Al elevar al cuadrado ocurre que no hace falta calcular el valor absoluto por lo que la fórmula es más común verla de la siguiente forma:
$$MSE = \frac{1}{N} \sum_{i=1}^{N}(y_{i} - \hat{y_{i}})^2$$
Su uso en Keras es:
model.compile(loss="mean_squared_error") model.compile(loss="mse") model.compile(loss=tf.keras.losses.mean_squared_error) model.compile(loss=tf.keras.losses.MeanSquaredError())
Mas información:
- Error Cuadrático Medio para Regresión: Explicación básica del Error Cuadrático Medio
Distancia del coseno
La distancia del coseno lo que calcula es en vez de la distancia entre 2 puntos, lo que hace es obtener el coseno de la diferencia entre sus ángulos.
Es decir que obtiene el ángulo que tiene cada vectos, resta esos ángulos y calcula el coseno.
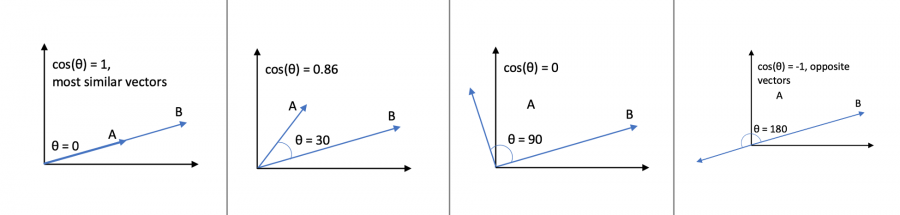
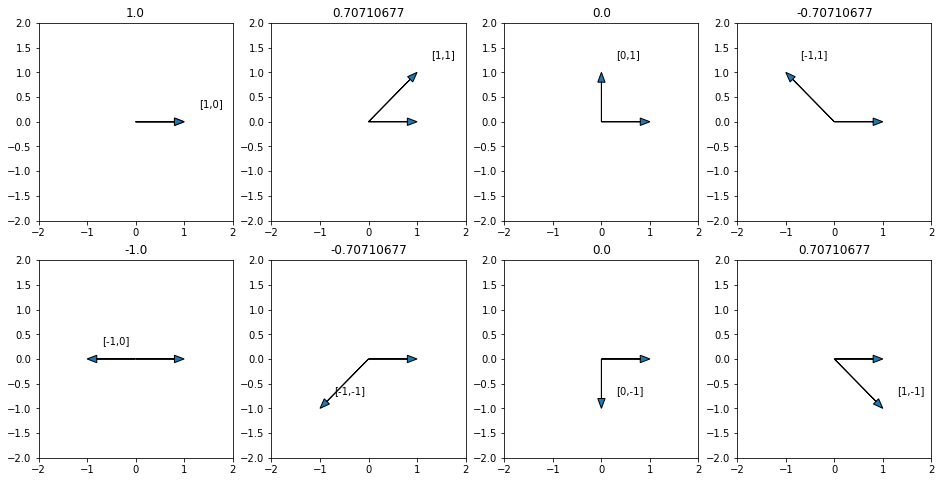
Veamos ahora valores del coseno de algunos ángulos:
- $cos(0 ^o )=1$
- $cos(45 ^o )=0,70711$
- $cos(90 ^o )=0$
- $cos(135 ^o )=-0,70711$
- $cos(180 ^o )=-1$
- $cos(225 ^o )=-0,70711$
- $cos(270 ^o )=0$
- $cos(315 ^o )=0,70711$
Si nos fijamos en la siguiente imagen en la que en la parte superior de cada par de vectores está el resultado de la distancia del coseno:
con un poco de ojo, podremos ver que los ángulos que forman y sus cosenos coinciden exactamente con la distancia entre los vectores.
Notar que si la resta de los ángulos es 0, es decir que son iguales, el resultado de 1, pero si forman un ángulo de 180° la diferencia es máxima, y su valor es -1. Por lo tanto la distancia del coseno está en el rango [-1,1].
Para hacer el cálculo matemáticamente podríamos usar algo de trigonometría, pero sería una forma muy costosa de calcularlo. En vez de eso, se usa la siguiente formula que es equivalente (Podemos ver la demostración aqui Cosine similarity: How does it measure the similarity, Maths behind and usage in Python):
$$ distancia \: del \: coseno=\frac{y \cdot \hat{y}}{ \| y \| \cdot \| \hat{y} \|}= \frac{\sum\limits_{i=1}^{N} y_{i} \cdot \hat{y_{i}}}{\sqrt{\sum\limits_{i=1}^{N}y_{i}^2} \cdot \sqrt{\sum\limits_{i=1}^{N}\hat{y_{i}}^2}} $$
En Python se hace de la siguiente forma:
y_true=np.array([ 1.0, 0.0]) y_pred=np.array([ 1.0, 0.2]) #Usando la fórmula con lo básico de numpy distancia_coseno_formula=np.sum(y_true*y_pred)/(np.sqrt(np.sum(y_true**2))*np.sqrt(np.sum(y_pred**2))) print(distancia_coseno_formula)
Y el resultado es éste:
0.9805806756909201
sin embargo si usamos la función de coste de Keras:
#Usando la función de coste de Keras distancia_coseno_keras=tf.keras.losses.cosine_similarity([y_true],[y_pred]).numpy()[0] print(distancia_coseno_keras)
-0.9805806756909201
Vemos que el resultado sale con el signo al revés. Esto es así porque las funciones de coste deben ser de forma que cuanto mayor es el valor, mayor es la diferencia entre $y$ e $\hat{y}$ . Así que simplemente la función de coste de tf.keras.losses.cosine_similarity es como la fórmula que hemos visto pero con un signo menos delante.
- Su uso en es Keras
model.compile(loss="cosine_similarity") model.compile(loss=tf.keras.losses.cosine_similarity) model.compile(loss=tf.keras.losses.CosineSimilarity())
Utilidad de la distancia del coseno
Acabamos de ver como funciona matemáticamente la distancia del coseno pero , ¿cual es su utilidad?
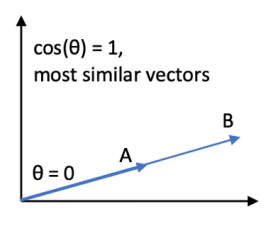
Primero veamos un posible problema de la distancia del coseno. Imaginemos los siguientes 2 vectores A y B
Los 2 vectores no son iguales pero la distancia del coseno nos dirá que son iguales ya que ambos tienen el mismo ángulo. Así que esta función de coste lo que le interesa es la dirección del vector y no el tamaño del vector. Pero, ¿donde puede eso ser últil? Veamos un ejemplo.
OpenPose es una librería que dado un vídeo, obtiene la posición de las personas.
Podemos definir la posición como un conjunto de vectores de cada una de las extremidades. El angulo de cada vector nos dice la posición de cada extremidad pero el tamaño del vector no dice el tamaño de la extremidad. Ahora veamos la siguiente imagen.
Son 3 personas distintas cada una con tamaños de extremidades distintas además que dependiendo de si están en la imagen más hacia el fondo, sus tamaños serán distintos. Para saber si las 3 están haciendo los mismos movimientos, ¿nos interesa que el tamaño de cada vector sea el mismo o nos interesa que los ángulos de cada vector sean los mismo? Obviamente lo que nos interesa es que el ángulo sea el mismo y no si el tamaño es el mismo.
Lo mismo se puede aplicar a un partido de papel:
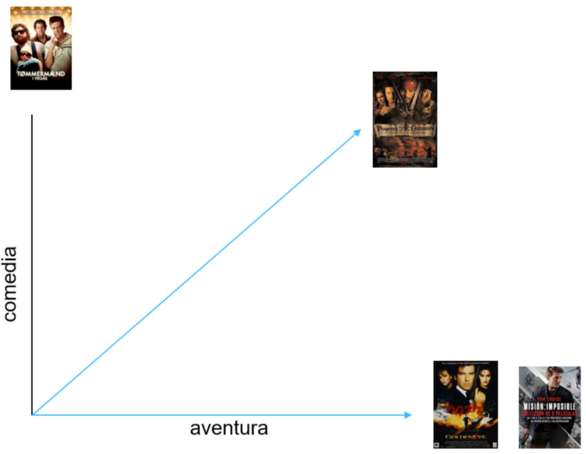
Otro ejemplo sería para catalogar películas de géneros semejantes. Veamos la siguiente gráfica:
En ángulo nos dice si la película tiene mas porcentaje de aventura o de comedia y la longitud como es de buena la película. Para buscar películas con géneros similares, ¿nos interesa que el tamaño del vector sea el mismo o nos interesa que el ángulo del vector sea el mismo? Como en el caso de antes nos interesa es que el ángulo sea el mismo y no si el tamaño es el mismo.
Otro uso común de la distancia del coseno el comprar si dos documentos se parecen según el Nº de palabras que tiene cada uno. Cada palabra es un vector n-dimensional y palabras similares tienen orientaciones similares. En este caso es necesario previamente tener una "base de datos" con todas las palabras codificadas como vectores. Podemos ver distintas bases de datos aquí:
Una explicación esto está en:
Mas información:
- Cosine similarity: How does it measure the similarity, Maths behind and usage in Python: Incluye la demostración de la fórmula
- How the Dot Product Measures Similarity: Explicación matemática de Similitud de coseno
Binary Cross Entropy
Las funciones de coste que hemos visto hasta ahora se usan en problemas de regresión, las siguientes funciones de coste que vamos a ver ahora se usan en problemas de clasificación.
La función de coste "Entropía cruzada binaria" o en inglés "Binary Cross Entropy" se usa en problemas de clasificación cuando solo hay 2 posibles resultados en la clasificación. Por ejemplo si una foto es o no una persona. Esta función de coste se suele usar junto a la función de activación "Sigmoide" como vimos en las funciones de activación.
La fórmula es la siguiente:
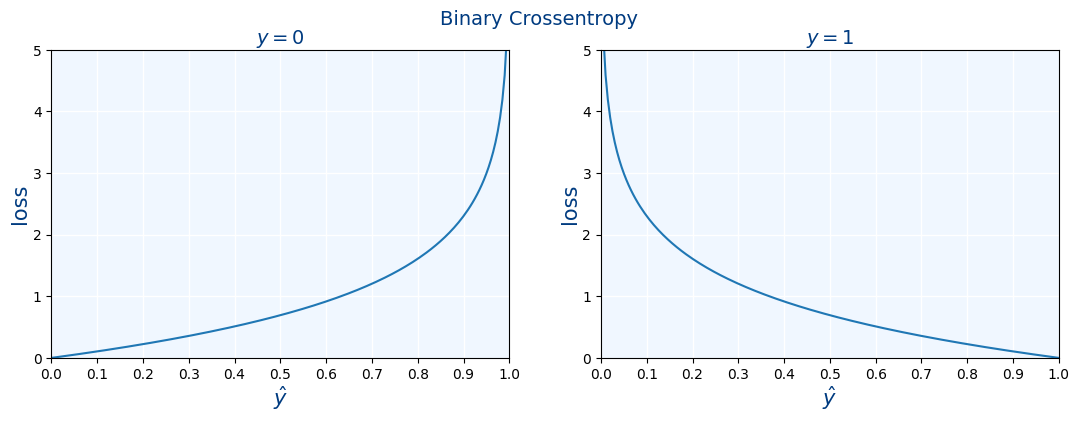
$$Binary \: Cross \: Entropy = - \frac{1}{N} \sum_{i=1}^{N} y_{i} \cdot log(\hat{y_i}) + (1-y_{i}) \cdot log(1-\hat{y_i}) $$
Los valores de $y_i$ suelen ser 0 o 1, mientras que los valores de $\hat{y_i}$ es un número real entre 0 y 1
Veamos ahora graficamente como es la fórmula según si $y=0$ o $y=1$
Su uso en Keras es:
model.compile(loss="binary_crossentropy") model.compile(loss=tf.keras.losses.binary_crossentropy) model.compile(loss=tf.keras.losses.BinaryCrossentropy())
Mas información:
Categorical Cross Entropy
La función de coste "Entropía cruzada categórica" o en inglés "Categorical Cross Entropy" se usa en problemas de clasificación cuando hay más de 2 resultados en la clasificación. Por ejemplo si una foto es un perro o un gato o una vaca.
Esta función de coste se suele usar junto a la función de activación "Softmax" como vimos en las funciones de activación. No vamos a poner su fórmula pero es una variación un poco más compleja de la fórmula de Binary Cross Entropy
Su uso en Keras es:
model.compile(loss="categorical_crossentropy") model.compile(loss=tf.keras.losses.categorical_crossentropy) model.compile(loss=tf.keras.losses.CategoricalCrossentropy())
Mas información:
Para acabar vamos a ver una tabla con la relación entre las funciones de activación usadas en la salida de una red neuronal y la función de coste que se podría usar.
| Problema | Función de Activación a la salida | Función de coste |
|---|---|---|
| Regresión | Lineal | MSE o Distancia del coseno |
| Clasificación con 2 posibles valores | Sigmoide | Binary Cross Entropy |
| Clasificación con más de 2 posibles valores NO excluyentes entre si | Sigmoide | Binary Cross Entropy |
| Clasificación con más de 2 posibles valores SI excluyentes entre si | Softmax | Categorical Cross Entropy |
Para terminar este apartado seguimos con nuestro ejemplo de red neuronal ahora incluyendo la función de coste:
iris=load_iris() x=iris.data[0:99,2] y_true=iris.target[0:99] np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() model.add(Dense(3, input_dim=1,activation=tf.keras.layers.LeakyReLU(),kernel_initializer="he_uniform")) model.add(Dense(1,activation="sigmoid")) model.compile(loss="binary_crossentropy")
Ejercicios
Ejercicio 1.A
En una red neuronal
- Estos son los valores que debería haber sacado la red
y_true=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
- Estos son los valores que realmente ha generado la red
y_pred=[0.18395704, 0.18395704, 0.18506491, 0.18799731, 0.18395704,
0.24096969, 0.18395704, 0.18799731, 0.18395704, 0.18799731,
0.18799731, 0.21094593, 0.18395704, 0.19304448, 0.18862939,
0.18799731, 0.18506491, 0.18395704, 0.24096969, 0.18799731,
0.24096969, 0.18799731, 0.19747499, 0.24096969, 0.30332845,
0.21094593, 0.21094593, 0.18799731, 0.18395704, 0.21094593,
0.21094593, 0.18799731, 0.18799731, 0.18395704, 0.18799731,
0.18862939, 0.18506491, 0.18395704, 0.18506491, 0.18799731,
0.18506491, 0.18506491, 0.18506491, 0.21094593, 0.30332845,
0.18395704, 0.21094593, 0.18395704, 0.18799731, 0.18395704,
0.95087045, 0.93909526, 0.9602022 , 0.89205027, 0.9452805 ,
0.93909526, 0.95087045, 0.75592554, 0.9452805 , 0.8777893 ,
0.8039025 , 0.9162346 , 0.89205027, 0.95087045, 0.82506734,
0.9322611 , 0.93909526, 0.9048277 , 0.93909526, 0.8777893 ,
0.955778 , 0.89205027, 0.9602022 , 0.95087045, 0.92472136,
0.9322611 , 0.955778 , 0.9638314 , 0.93909526, 0.8039025 ,
0.8619356 , 0.8443901 , 0.8777893 , 0.96697116, 0.93909526,
0.93909526, 0.95087045, 0.9322611 , 0.9048277 , 0.89205027,
0.9322611 , 0.9452805 , 0.89205027, 0.75592554, 0.9162346 ,
0.9162346 , 0.9162346 , 0.92472136, 0.6703734 ]
Haz un programa en python que calcule mediante las fórmulas la pérdida de la red con MAE, MSE y Binary Cross Entropy
Ejercicio 1.B
Repita el ejercicio anterior pero ahora en vez de usar su código en python, usan las funciones de coste de keras:
tf.keras.losses.mean_absolute_errortf.keras.losses.mean_squared_errortf.keras.losses.categorical_crossentropy
Ejercicio 2
Tenemos dos redes neuronales, que deberían haber sacado los siguientes datos.
y_true=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
- La red A ha sacado los siguientes datos:
y_pred_red_a=[0.18395704, 0.18395704, 0.18506491, 0.18799731, 0.18395704,
0.24096969, 0.18395704, 0.18799731, 0.18395704, 0.18799731,
0.18799731, 0.21094593, 0.18395704, 0.19304448, 0.18862939,
0.18799731, 0.18506491, 0.18395704, 0.24096969, 0.18799731,
0.24096969, 0.18799731, 0.19747499, 0.24096969, 0.30332845,
0.21094593, 0.21094593, 0.18799731, 0.18395704, 0.21094593,
0.21094593, 0.18799731, 0.18799731, 0.18395704, 0.18799731,
0.18862939, 0.18506491, 0.18395704, 0.18506491, 0.18799731,
0.18506491, 0.18506491, 0.18506491, 0.21094593, 0.30332845,
0.18395704, 0.21094593, 0.18395704, 0.18799731, 0.18395704,
0.95087045, 0.93909526, 0.9602022 , 0.89205027, 0.9452805 ,
0.93909526, 0.95087045, 0.75592554, 0.9452805 , 0.8777893 ,
0.8039025 , 0.9162346 , 0.89205027, 0.95087045, 0.82506734,
0.9322611 , 0.93909526, 0.9048277 , 0.93909526, 0.8777893 ,
0.955778 , 0.89205027, 0.9602022 , 0.95087045, 0.92472136,
0.9322611 , 0.955778 , 0.9638314 , 0.93909526, 0.8039025 ,
0.8619356 , 0.8443901 , 0.8777893 , 0.96697116, 0.93909526,
0.93909526, 0.95087045, 0.9322611 , 0.9048277 , 0.89205027,
0.9322611 , 0.9452805 , 0.89205027, 0.75592554, 0.9162346 ,
0.9162346 , 0.9162346 , 0.92472136, 0.6703734 ]
- La red B, ha sacado los siguientes datos:
y_pred_red_b=[0.1359098 , 0.1359098 , 0.13724494, 0.1496709 , 0.1359098 ,
0.20224485, 0.1359098 , 0.1496709 , 0.1359098 , 0.1496709 ,
0.1496709 , 0.17425027, 0.1359098 , 0.14369074, 0.13939261,
0.1496709 , 0.13724494, 0.1359098 , 0.20224485, 0.1496709 ,
0.20224485, 0.1496709 , 0.14819524, 0.20224485, 0.27304262,
0.17425027, 0.17425027, 0.1496709 , 0.1359098 , 0.17425027,
0.17425027, 0.1496709 , 0.1496709 , 0.1359098 , 0.1496709 ,
0.13939261, 0.13724494, 0.1359098 , 0.13724494, 0.1496709 ,
0.13724494, 0.13724494, 0.13724494, 0.17425027, 0.27304262,
0.1359098 , 0.17425027, 0.1359098 , 0.1496709 , 0.1359098 ,
0.98840487, 0.98393154, 0.99160326, 0.95883477, 0.9863478 ,
0.98393154, 0.98840487, 0.854748 , 0.9863478 , 0.9503383 ,
0.8971007 , 0.97183764, 0.95883477, 0.98840487, 0.9138802 ,
0.98081565, 0.98393154, 0.9659298 , 0.98393154, 0.9503383 ,
0.99015427, 0.95883477, 0.99160326, 0.98840487, 0.97674596,
0.98081565, 0.99015427, 0.99284065, 0.98393154, 0.8971007 ,
0.9401976 , 0.92814255, 0.9503383 , 0.9938967 , 0.98393154,
0.98393154, 0.98840487, 0.98081565, 0.9659298 , 0.95883477,
0.98081565, 0.9863478 , 0.95883477, 0.854748 , 0.97183764,
0.97183764, 0.97183764, 0.97674596, 0.76543546]
Calcula la pérdida de las 2 redes con MAE, MSE y Binary Cross Entropy (mediante las funciones de Keras).
| MAE | MSE | Binary Cross Entropy | |
|---|---|---|---|
| Red A | |||
| Red B |
¿cual es mejor red? Explica porqué
Ejercicio 3
Usando los siguientes datos:
iris=load_iris() x=np.array(iris.data[0:99,2]) y_true=np.array(iris.target[0:99])
Y con la siguiente red neuronal:
model=Sequential()
model.add(Dense(2, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(4, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(8, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(16, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(8, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(4, input_dim=1,activation=tf.keras.layers.LeakyReLU()))
model.add(Dense(1,activation="sigmoid"))
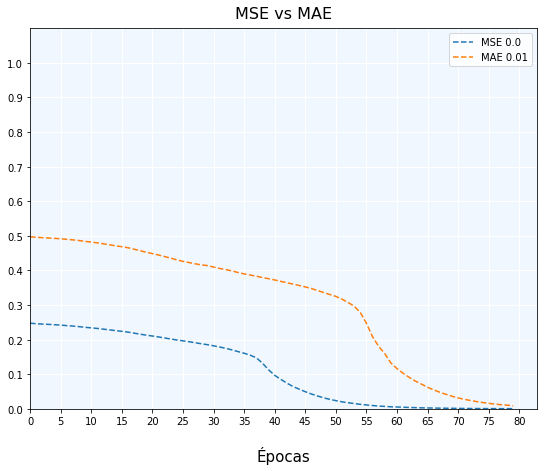
Entrena la red durante 80 épocas, usando MAE y vuelve a entrenar la red usando MSE
Muestra una gráfica similar a la siguiente:
En este tema ya hemos aprendido que la función de perdida para este ejemplo debe ser Binary Cross Entropy pero seguimos usando
MAE y MSE porque son más fáciles de calcular manualmente por el alumno en los ejercicios.
Ejercicio 4
Usando los siguientes datos:
iris=load_iris() x=np.array(iris.data[0:99,2]) y_true=np.array(iris.target[0:99])
Y con la siguiente red neuronal:
model=Sequential() model.add(Dense(3, input_dim=1,activation="relu")) model.add(Dense(1,activation="sigmoid")) model.compile(loss="mse")
Entrena la red durante 80 épocas, usando MSE y obtén:
- La pérdida de
MSEque obtenemos con el métodosfit. Será la de la última época. - Obtén el array
y_predcon el métodopredict- Calcula manualmente mediante las fórmulas la pérdida de
MSE - Calcula mediante las funciones de Keras la pérdida de
MSE
Comprueba si las 3 pérdidas tienen el mismo valor.
En este tema ya hemos aprendido que la función de perdida para este ejemplo debe ser Binary Cross Entropy pero seguimos usando
MAE y MSE porque son más fáciles de calcular manualmente por el alumno en los ejercicios.
Ejercicio 5.A
Vamos a comprobar como funciona la distancia del coseno para textos. Para ello vamos a obtener una base de datos con 1.692.025 palabras organizadas en vectores de 300 dimensiones.
Para prepararlo todo, antes hay que hacer lo siguiente
- Descarga el fichero SBW-vectors-300-min5.bin.gz, que se creo en Spanish Billion Word Corpus and Embeddings
- Descomprime el fichero y obtendrás el nuevo fichero llamado
sbwce.wordvectors.all.bin - Instala el paquete de python llamado
gensim.
Ahora desde python vamos a usarlo:
- Importa el siguiente código:
from gensim.models import KeyedVectors from gensim.test.utils import datapath
- Carga el fichero
wv = KeyedVectors.load_word2vec_format(datapath("sbwce.wordvectors.all.bin"), binary=True)
- Muestra el número exacto de palabras que tiene
len(wv)
- El método
similaritydel objetovwobtiene la distancia del coseno entre 2 palabras
wv.similarity('padre', 'madre')
0.85508734
Ejercicio 5.B
Siguiendo con el ejercicio anterior. Muestra la distancia del coseno entre los siguientes pares de palabras:
- verdura , lechuga
- tigre , gato
- movil , android
- tiburón , libro
- matemáticas , hijo
Ejercicio 5.C
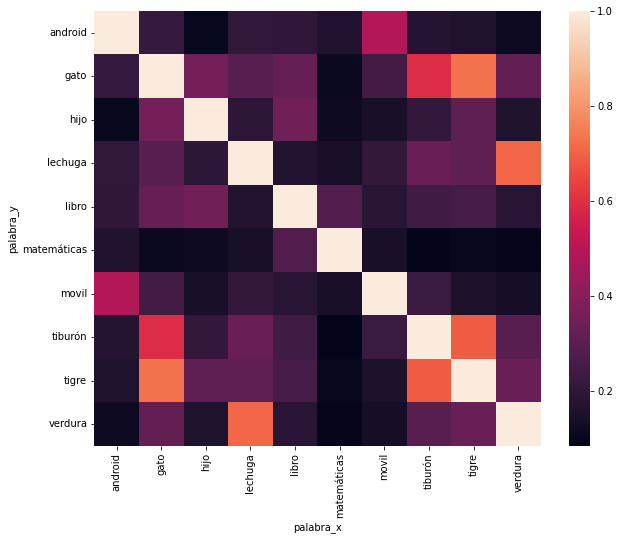
Siguiendo con el ejercicio anterior. Crea un heatmap usando Seaborn con la distancia del coseno de todas las anteriores palabras.
Deberás crear un dataframe con las columnas:
palabra_xpalabra_ydistancia_coseno
y ejecutar la siguiente línea para que transforme el DataFrame en una matriz válida para hacer el heatmap:
df = df.pivot(index='palabra_y', columns='palabra_x', values='distancia_coseno')
muestra el heatmap
sns.heatmap(df,ax=axes)
Ejercicio 5.D
Siguiendo con el ejercicio anterior.
- Ejecuta la siguiente línea. ¿que crees que hace?
wv.most_similar_cosmul(positive=['rey'])
- Ejecuta la siguiente línea. ¿Como se ha modificado el resultado?
wv.most_similar_cosmul(positive=['rey','mujer'])
- Ejecuta la siguiente línea. ¿Como se ha modificado el resultado?
wv.most_similar_cosmul(positive=['rey','mujer'],negative=['hombre'])
Ejercicio 5.E
¿Le has visto alguna utilidad a tener las palabras como vectores y que se puedan relacionar entre ellas? Piensa algún proyecto donde se pudiera usar.
Ejercicio 6
Dado los siguientes problemas de redes neuronales, indica la función (o funciones) de pérdida que usarías:
- Obtener el consumo de un coche según las distintas condiciones climáticas, la carretera y el tipo de coche
- Averiguar si un paciente tendrá diabetes en el futuro según una serie de analíticas que se han ido haciendo a lo largo de su vida.
- Distinguir entre 5 tipos de vino según distintas características del vino
- Indicar las variedades de olivas que lleva un aceite y su proporción según el análisis químico que se le hace al aceite.
- Indicar si una compra con tarjeta es fraudulenta
- Averiguar a que partido político ha votado una persona
- Averiguar la distancia a la que se encuentra una estrella según diversas fotos que se van sacando de ella con telescopios.
- Entre 8 tipos distintos de canceres y dada la foto de las células de una persona averiguar los cánceres que puede tener
- Saber el tipo de tiburón según el sonido que hace bajo el agua al desplazarse
- Calcular la ubicación de los objetivos a destruir por un tanque según los sensores proporcionados por el tanque
- Averiguar la cifra que se ha escrito una persona a mano.
Ejercicio 7
Crea una red neuronal para entrenar las flores. Tienes que entrenarla durante 300 épocas con todas las combinaciones de:
- Estructura de la red:
- [3]
- [4, 3]
- [4, 8, 3]
- [4, 8, 16, 8, 3]
- [4, 8, 16, 32, 16, 8, 4, 3]
- [4, 8, 16, 32, 64, 32, 16, 8, 4, 3]
- [4, 8, 16, 32, 64, 128, 64, 32, 16, 8, 4, 3]
- Funciones de activación:
- Sigmoid
- Tanh
- ReLU
- LeakyReLU
- SeLU
- ELU
Responde las siguientes cuestiones:
- ¿Cual ha resultado ser la mejor estructura de red?
- ¿Cual ha sido la mejor función de activación para la mejor estructura de red?
Ejercicio 8.A
Crea y entrena una red neuronal que averigüe si un paciente tendrá diabetes. Los datos los obtendrás con la función load_diabetes.
from sklearn.datasets import load_diabetes
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- Elegir adecuadamente la función de coste a usar
Ejercicio 8.B
Crea y entrena una red neuronal que averigüe el dígito que ha escrito una persona. Los datos los obtendrás con la función load_digits.
from sklearn.datasets import load_digits
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- Elegir adecuadamente la función de coste a usar
Ejercicio 8.C
Crea y entrena una red neuronal que averigüe el tipo de un vino. Los datos los obtendrás con la función load_wine.
from sklearn.datasets import load_wine
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- Elegir adecuadamente la función de coste a usar
Ejercicio 8.D
Crea y entrena una red neuronal que averigüe si tiene cáncer de mama. Los datos los obtendrás con la función load_breast_cancer.
from sklearn.datasets import load_breast_cancer
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- Elegir adecuadamente la función de coste a usar
clase/iabd/pia/2eval/tema07.txt · Última modificación: 2024/01/30 15:26 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3