Herramientas de usuario
Ocultar Menú
Traza:
−Barra lateral
clase:iabd:pia:2eval:tema07-apendices-metricas
¡Esta es una revisión vieja del documento!
7. Entrenamiento de redes neuronales e) Apéndices Métricas
En este apartado vamos a ampliar las métricas que podemos usar con la clasificación binaria las cuales ya vimos en tema07.metricas.
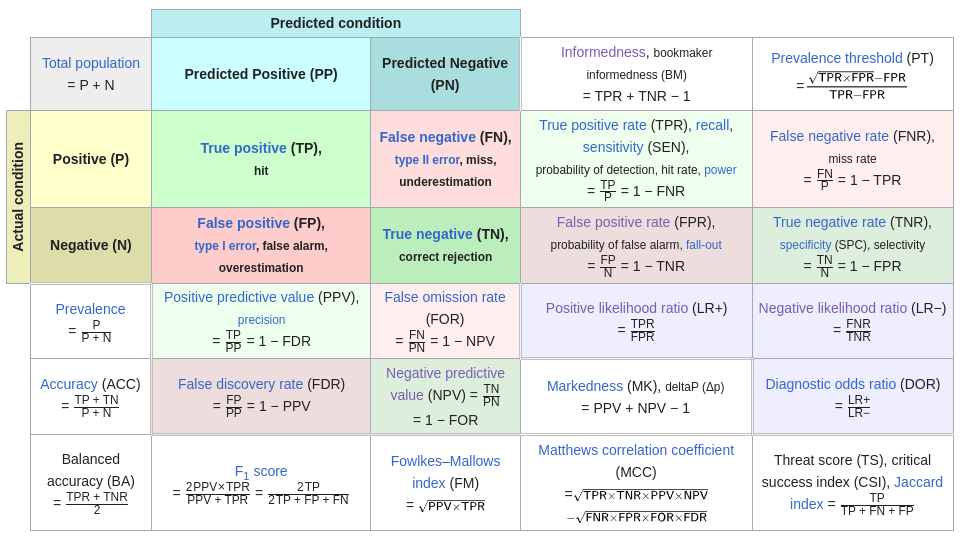
Para ampliar nos vamos a basar en este diagrama (que se puede ver en Matriz de confusión en Wikipedia)
Las métricas que ya las hemos explicado en el tema de métricas son:
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas según el teorema de bayes (PPV,NPV, FDR y FOR)
Las métricas que ahora vamos a ver son métricas que hacen la media entre alguna de las dos métricas que acabamos de indicar.
Para organizar las métricas según 2 criterios:
- Según que métricas juntan
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas (PPV,NPV, FDR y FOR)
- Métricas mixtas, que usa una básica y otra derivada.
- Según la fórmula que usan:
- Media aritmética
- Media armónica
- Media geométrica
- Suma-1
- Ratio
Juntado dos Métricas Básicas
Las 4 métricas básicas son Sensibilidad, Especificidad, FPR y FNR. Según eso existen las siguientes métricas:
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| Sensibilidad (TPR) y Especificidad (TNR) | BalancedAccuracy=TPR+TNR2 | Informedness=TPR+TNR−1 | |||
| Sensibilidad (TPR) y FPR | Positivelikelihoodratio=TPRFPR | ||||
| Especificidad (TNR) y FNR | Negativelikelihoodratio=FNRTNR | ||||
| FPR y FNR | |||||
Mas información:
- Youden Index and the optimal threshold for markers with mass at zero: El indice Youden es el máximo Informedness según el threshold
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| Sensibilidad (TPR) y Especificidad (TNR) | 11TPR+1TNR | √TPR∗TNR | TPRTNR y TNRTPR | ||
| Sensibilidad (TPR) y FPR | TPR+FPR2 | 11TPR+1FPR | √TPR∗FPR | TPR+FPR−1 | FPRTPR |
| Especificidad (TNR) y FNR | TNR+FNR2 | 11TNR+1FNR | √TNR∗FNR | TNR+FNR−1 | TNRFNR |
| FPR y FNR | FPR+FNR2 | 11FPR+1FNR | √FPR∗FNR | FPR+FNR−1 | FNRFPR y FPRFNR |
No tiene sentido que se junten las métricas de TPR y FNR o las métricas de FPR y TNR ya que entre ellas son complementarias. Es decir que TPR+FNR=1 y que FPR+TNR=1
Juntado dos Métricas derivadas
Las 4 métricas derivadas son PPV, NPV, FDR y FOR.
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y NPV | Markdness=PPV+NPV−1 | ||||
| PPV y FOR | |||||
| NPV y FDR | |||||
| FDR y FOR | |||||
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y NPV | PPV+NPV2 | 11PPV+1NPV | √PPV∗NPV | PPVNPV y NPVPPV | |
| PPV y FOR | PPV+FOR2 | 11PPV+1FOR | √PPV∗FOR | PPV+FOR−1 | PPVFOR y FORPPV |
| NPV y FDR | NPV+FDR2 | 11NPV+1FDR | √NPV∗FDR | NPV+FDR−1 | NPVFDR y FDRNPV |
| FDR y FOR | FDR+FOR2 | 11FDR+1FOR | √FDR∗FOR | FDR+FOR−1 | FDRFOR y FORFDR |
No tiene sentido que se junten las métricas de PPV y FDR o las métricas de NPV y FOR ya que entre ellas son complementarias. Es decir que PPV+FDR=1 y que NPV+FOR=1
Métricas mixtas
Son métricas que juntan una métrica básica con una métrica derivada. Debido a que existen 16 combinaciones no vamos a mostrar todas las que existen, sino solo las que he considerado interesantes.
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y Sensibilidad (TPR) | F1score=11PPV+1TPR | Fowlkes−Mallowsindex=√PPV∗TPR | |||
| NPV y Especificidad (TNR) | |||||
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y Sensibilidad (TPR) | PPV+TPR2 | PPV+TPR−1 | PPVTPR y TPRPPV | ||
| NPV y Especificidad (TNR) | NPV+TNR2 | 11NPV+1TNR | √NPV∗TNR | NPV+TNR−1 | NPVTNR y TNRNPV |
Más métricas derivadas
Veamos ahora otras métricas que derivamos a partir de las básicas.
Accuracy
Accuracy (Exactitud) mide la proporción de predicciones correctas sobre el total de predicciones realizadas. Por lo que su fórmula es:
Accuracy=TP+TNTP+FN+FP+TN
Debido a que usa los 4 valores vamos a expresar la misma fórmula usando Especificidad, Sensibilidad y Prevalencia. Esto se hace ya que así podremos usar la prevalencia que queramos y no la de nuestros datos.
Accuracy=P(Prediccióncorrecta|Predicciónrealizada)
Eso se puede expresar como la suma de 2 probabilidades
P(Prediccióncorrecta|Predicciónrealizada)=P(Positivo∩Enfermo)+P(Negativo∩Sano)=
P(Positivo|Enfermo)∗P(Enfermo)+P(Negativo|Sano)∗P(Sano)=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)
Vamos a ver que para la prevalencia de los datos, las 2 fórmulas son iguales.
Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)=TP(TP+FN)∗(TP+FN)TP+FN+FP+TN+TN(FP+TN)∗(FP+TN)TP+FN+FP+TN=
TPTP+FN+FP+TN+TNTP+FN+FP+TN=TP+TNTP+FN+FP+TN=Accuracy
Por lo tanto:
Accuracy=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)
Accuracy y Balanced Accuracy
Realmente esta no es una nueva métrica sino que es la misma que Accuracy pero con una prevalencia del 0.5
BalancedAccuracy=Sensibilidad+Especificidad2
Pero si calculamos Accuracy suponiendo que la Prevalencia=0.5 obtenemos:
Accuracy=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)=
Sensibilidad∗0,5+Especificidad∗(1−0,5)=Sensibilidad∗0,5+Especificidad∗0,5=
Sensibilidad2+Especificidad2=Sensibilidad+Especificidad2=BalancedAccuracy
Indice Jaccard
Este índice es la división entre 2 probabilidades:
IndiceJaccard=P(Positivo∩Enfermo)P(Positivo∪Enfermo)=TPTP+FP+FN
- Se deduce de la siguiente forma:
P(Positivo∩Enfermo)P(Positivo∪Enfermo)=
P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo∩Enfermo)=P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo|Enfermo)∗P(Enfermo)
- Sabiendo que:
P(Enfermo)=TP+FNTP+FN+FP+TNP(Sano)=FP+TNTP+FN+FP+TNP(Positivo)=TP+FPTP+FN+FP+TNP(Negativo)=FN+TNTP+FN+FP+TNP(Positivo|Enfermo)=TPTP+FN
- Entonces:
P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo|Enfermo)∗P(Enfermo)=
(TPTP+FN∗TP+FNTP+FN+FP+TN)÷(TP+FPTP+FN+FP+TN+TP+FNTP+FN+FP+TN−TPTP+FN∗TP+FNTP+FN+FP+TN)=
(TPTP+FN+FP+TN)÷(TP+FPTP+FN+FP+TN+TP+FNTP+FN+FP+TN−TPTP+FN+FP+TN)=
(TPTP+FN+FP+TN)÷(TP+FP+TP+FN−TPTP+FN+FP+TN)=(TPTP+FN+FP+TN)÷(TP+FP+FNTP+FN+FP+TN)=
TPTP+FP+FN=IndiceJaccard
- Sin embargo también podemos definir el Indice Jaccard en función de la sensibilidad, la especificidad y la prevalencia.Usando el teorema de bayes podemos definir P(Positivo) de la siguiente forma:
P(Positivo)=P(Positivo|Enfermo)∗P(Enfermo)P(Enfermo|Positivo)=
P(Positivo|Enfermo)∗P(Enfermo)1÷P(Positivo|Enfermo)∗P(Enfermo)P(Positivo|Enfermo)∗P(Enfermo)+P(Positivo|Sano)∗P(Sano)=
Sensibilidad∗Prevalencia+(1−Especificidad)∗(1−Prevalencia)
- Y ahora usamos la formula de P(Positivo) en la definición del Indice Jaccard
Indice \; Jaccard=\frac{P(Positivo|Enfermo)*P(Enfermo)}{P(Positivo)+P(Enfermo)-P(Positivo|Enfermo)*P(Enfermo)}=
\frac{Sensibilidad*Prevalencia}{Sensibilidad*Prevalencia+(1-Especificidad)*(1-Prevalencia)+Prevalencia-Sensibilidad*Prevalencia}=
\frac{Sensibilidad*Prevalencia}{(1-Especificidad)*(1-Prevalencia)+Prevalencia}
- Por lo tanto
Indice \; Jaccard=\frac{Sensibilidad*Prevalencia}{(1-Especificidad)*(1-Prevalencia)+Prevalencia}
Prevalence threshold
La métrica de Prevalence threshold está explicada en Prevalence threshold (ϕe) and the geometry of screening curves.
Lo único que diremos respecto a la formula es que en el artículo aparece como:
Prevalence \; threshold=\frac{\sqrt{Sensibilidad(1-Especificidad)}+(Especificidad-1)}{Sensibilidad+Especificidad+1} Que jugando un poco con los signos se obtiene la formula equivalente: Prevalence \; threshold=\frac{\sqrt{Sensibilidad*FPR}-FPR}{Sensibilidad-FPR}
Matthews correlation coefficient
Es otra métrica pero que tiene en cuenta que los datos no estén balanceados.
El MMC tiene un valor entre -1 a 1. Siendo:
- 1 : El clasificador funciona perfectamente
- 0 : El clasificador acierta aleatoriamente
- -1 : El clasificador acierta peor que aleatoriamente, es decir que clasifica al revés "perfectamente"
MCC = \frac{ \mathit{TP} \times \mathit{TN} - \mathit{FP} \times \mathit{FN} } {\sqrt{ (\mathit{TP} + \mathit{FP}) ( \mathit{TP} + \mathit{FN} ) ( \mathit{TN} + \mathit{FP} ) ( \mathit{TN} + \mathit{FN} ) } }=\sqrt{TPR \times TNR \times PPV \times NPV}-\sqrt{FNR \times FPR \times FOR \times FDR}
Podemos hacer uso de la métrica con la función sklearn.metrics.matthews_corrcoef de sklearn
Ejemplo de uso:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from sklearn.metrics import matthews_corrcoefy_true = [1,1,1,1,0,0,0,0]y_pred = [1,1,1,1,0,0,0,0]print("Valor para una predicción que acierta siempre=",matthews_corrcoef(y_true,y_pred))y_true = [1,1,1,1,0,0,0,0]y_pred = [1,1,0,0,1,1,0,0]print("Valor para una predicción que acierta la mitad=",matthews_corrcoef(y_true,y_pred))y_true = [1,1,1,1,0,0,0,0]y_pred = [0,0,0,0,1,1,1,1]print("Valor para una predicción que nunca acierta=",matthews_corrcoef(y_true,y_pred)) |
Valor para una predicción que acierta siempre= 1.0 Valor para una predicción que acierta la mitad= 0.0 Valor para una predicción que nunca acierta= -1.0
Mas información:
clase/iabd/pia/2eval/tema07-apendices-metricas.1710065993.txt.gz · Última modificación: 2024/03/10 11:19 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3