Herramientas de usuario
Ocultar Menú
Traza:
−Barra lateral
clase:iabd:pia:2eval:tema07-apendices-metricas
¡Esta es una revisión vieja del documento!
7. Entrenamiento de redes neuronales e) Apéndices Métricas
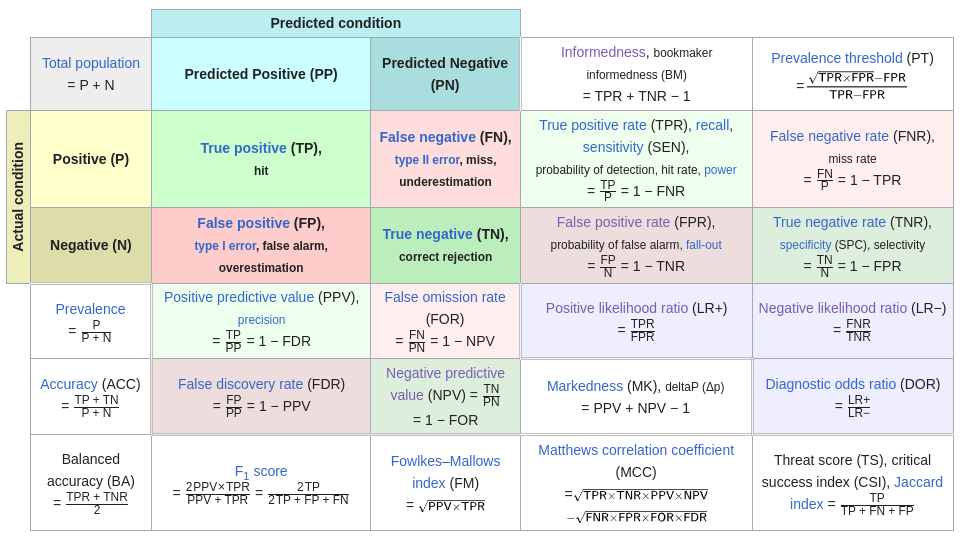
En este apartado vamos a ampliar las métricas que podemos usar con la clasificación binaria las cuales ya vimos en tema07.metricas.
Para ampliar nos vamos a basar en este diagrama (que se puede ver en Matriz de confusión en Wikipedia)
Las métricas que ya las hemos explicado en el tema de métricas son:
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas según el teorema de bayes (PPV,NPV, FDR y FOR)
Las métricas que ahora vamos a ver son métricas que hacen la media entre alguna de las dos métricas que acabamos de indicar.
Para organizar las métricas según 2 criterios:
- Según que métricas juntan
- Métricas básicas (Sensibilidad, Especificidad, FNR y FPR)
- Métricas derivadas (PPV,NPV, FDR y FOR)
- Métricas mixtas, que usa una básica y otra derivada.
- Según la fórmula que usan:
- Media aritmética
- Media armónica
- Media geométrica
- Suma-1
- Ratio
Juntado dos Métricas Básicas
Las 4 métricas básicas son Sensibilidad, Especificidad, FPR y FNR. Según eso existen las siguientes métricas:
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| Sensibilidad (TPR) y Especificidad (TNR) | BalancedAccuracy=TPR+TNR2 | Informedness=TPR+TNR−1 | |||
| Sensibilidad (TPR) y FPR | Positivelikelihoodratio=TPRFPR | ||||
| Especificidad (TNR) y FNR | Negativelikelihoodratio=FNRTNR | ||||
| FPR y FNR | |||||
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| Sensibilidad (TPR) y Especificidad (TNR) | 11TPR+1TNR | √TPR∗TNR | TPRTNR y TNRTPR | ||
| Sensibilidad (TPR) y FPR | TPR+FPR2 | 11TPR+1FPR | √TPR∗FPR | TPR+FPR−1 | FPRTPR |
| Especificidad (TNR) y FNR | TNR+FNR2 | 11TNR+1FNR | √TNR∗FNR | TNR+FNR−1 | TNRFNR |
| FPR y FNR | FPR+FNR2 | 11FPR+1FNR | √FPR∗FNR | FPR+FNR−1 | FNRFPR y FPRFNR |
No tiene sentido que se junten las métricas de TPR y FNR o las métricas de FPR y TNR ya que entre ellas son complementarias. Es decir que TPR+FNR=1 y que FPR+TNR=1
Juntado dos Métricas derivadas
Las 4 métricas derivadas son PPV, NPV, FDR y FOR.
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y NPV | Markdness=PPV+NPV−1 | ||||
| PPV y FOR | |||||
| NPV y FDR | |||||
| FDR y FOR | |||||
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y NPV | PPV+NPV2 | 11PPV+1NPV | √PPV∗NPV | PPVNPV y NPVPPV | |
| PPV y FOR | PPV+FOR2 | 11PPV+1FOR | √PPV∗FOR | PPV+FOR−1 | PPVFOR y FORPPV |
| NPV y FDR | NPV+FDR2 | 11NPV+1FDR | √NPV∗FDR | NPV+FDR−1 | NPVFDR y FDRNPV |
| FDR y FOR | FDR+FOR2 | 11FDR+1FOR | √FDR∗FOR | FDR+FOR−1 | FDRFOR y FORFDR |
No tiene sentido que se junten las métricas de PPV y FDR o las métricas de NPV y FOR ya que entre ellas son complementarias. Es decir que PPV+FDR=1 y que NPV+FOR=1
Métricas mixtas
Son métricas que juntan una métrica básica con una métrica derivada. Debido a que existen 16 combinaciones no vamos a mostrar todas las que existen, sino solo las que he considerado interesantes.
- La siguiente tabla son métricas que existen (Tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y Sensibilidad (TPR) | F1score=11PPV+1TPR | Fowlkes−Mallowsindex=√PPV∗TPR | |||
| NPV y Especificidad (TNR) | |||||
- La siguiente tabla son métricas que no existen (No tienen nombre)
| Fórmula que usan | |||||
|---|---|---|---|---|---|
| Métricas básicas que usan | Media aritmética | Media armónica | Media geométrica | Suma-1 | Ratio |
| PPV y Sensibilidad (TPR) | PPV+TPR2 | PPV+TPR−1 | PPVTPR y TPRPPV | ||
| NPV y Especificidad (TNR) | NPV+TNR2 | 11NPV+1TNR | √NPV∗TNR | NPV+TNR−1 | NPVTNR y TNRNPV |
Otras métricas
Veamos ahora otras métricas que si que existen pero no encajan en organización que habíamos creado.
Accuracy
Accuracy (Exactitud) mide la proporción de predicciones correctas sobre el total de predicciones realizadas. Por lo que su fórmula es:
Accuracy=TP+TNTP+FN+FP+TN
Debido a que usa los 4 valores vamos a expresar la misma fórmula usando Especificidad, Sensibilidad y Prevalencia. Esto se hace ya que así podremos usar la prevalencia que queramos y no la de nuestros datos.
Accuracy=P(Prediccióncorrecta|Predicciónrealizada)
Eso se puede expresar como la suma de 2 probabilidades
P(Prediccióncorrecta|Predicciónrealizada)=P(Positivo∩Enfermo)+P(Negativo∩Sano)=
P(Positivo|Enfermo)∗P(Enfermo)+P(Negativo|Sano)∗P(Sano)=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)
Vamos a ver que para la prevalencia de los datos, las 2 fórmulas son iguales.
Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)=TP(TP+FN)∗(TP+FN)TP+FN+FP+TN+TN(FP+TN)∗(FP+TN)TP+FN+FP+TN=
TPTP+FN+FP+TN+TNTP+FN+FP+TN=TP+TNTP+FN+FP+TN=Accuracy
Por lo tanto:
Accuracy=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)
Accuracy y Balanced Accuracy
Veamos ahora la relación que hay entre Accuracy y Balanced Accuracy.
BalancedAccuracy=Sensibilidad+Especificidad2
Pero si calculamos Accuracy suponiendo que la Prevalencia=0.5 obtenemos:
Accuracy=Sensibilidad∗Prevalencia+Especificidad∗(1−Prevalencia)=
Sensibilidad∗0,5+Especificidad∗(1−0,5)=Sensibilidad∗0,5+Especificidad∗0,5=
Sensibilidad2+Especificidad2=Sensibilidad+Especificidad2=BalancedAccuracy
Indice Jaccard
Este índice es la división entre 2 probabilidades:
IndiceJaccard=P(Positivo∩Enfermo)P(Positivo∪Enfermo)=TPTP+FP+FN
Se deduce de la siguiente forma:
P(Positivo∩Enfermo)P(Positivo∪Enfermo)=
P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo∩Enfermo)=P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo|Enfermo)∗P(Enfermo)
Sabiendo que:
P(Enfermo)=TP+FNTP+FN+FP+TNP(Sano)=FP+TNTP+FN+FP+TNP(Positivo)=TP+FPTP+FN+FP+TNP(Negativo)=FN+TNTP+FN+FP+TNP(Positivo|Enfermo)=TPTP+FN
Entonces:
P(Positivo|Enfermo)∗P(Enfermo)P(Positivo)+P(Enfermo)−P(Positivo|Enfermo)∗P(Enfermo)=
(TPTP+FN∗TP+FNTP+FN+FP+TN)÷(TP+FPTP+FN+FP+TN+TP+FNTP+FN+FP+TN−TPTP+FN∗TP+FNTP+FN+FP+TN)=
(TPTP+FN+FP+TN)÷(TP+FPTP+FN+FP+TN+TP+FNTP+FN+FP+TN−TPTP+FN+FP+TN)=
(TPTP+FN+FP+TN)÷(TP+FP+TP+FN−TPTP+FN+FP+TN)=(TPTP+FN+FP+TN)÷(TP+FP+FNTP+FN+FP+TN)=
TPTP+FP+FN=IndiceJaccard
Prevalence threshold
La métrica de Prevalence threshold está explicada en Prevalence threshold (ϕe) and the geometry of screening curves.
Lo único que diremos respecto a la formula es que en el artículo aparece como:
Prevalencethreshold=√Sensibilidad(1−Especificidad)+(Especificidad−1)Sensibilidad+Especificidad+1 Que jugando un poco con los signos se obtiene la formula equivalente: Prevalencethreshold=√Sensibilidad∗FPR−FPRSensibilidad−FPR
Matthews correlation coefficient
Es otra métrica pero que tiene en cuenta que los datos no estén balanceados.
El MMC tiene un valor entre -1 a 1. Siendo:
- 1 : El clasificador funciona perfectamente
- 0 : El clasificador acierta aleatoriamente
- -1 : El clasificador acierta peor que aleatoriamente, es decir que clasifica al revés "perfectamente"
MCC=TP×TN−FP×FN√(TP+FP)(TP+FN)(TN+FP)(TN+FN)=√TPR×TNR×PPV×NPV−√FNR×FPR×FOR×FDR
Podemos hacer uso de la métrica con la función sklearn.metrics.matthews_corrcoef de sklearn
Ejemplo de uso:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from sklearn.metrics import matthews_corrcoefy_true = [1,1,1,1,0,0,0,0]y_pred = [1,1,1,1,0,0,0,0]print("Valor para una predicción que acierta siempre=",matthews_corrcoef(y_true,y_pred))y_true = [1,1,1,1,0,0,0,0]y_pred = [1,1,0,0,1,1,0,0]print("Valor para una predicción que acierta la mitad=",matthews_corrcoef(y_true,y_pred))y_true = [1,1,1,1,0,0,0,0]y_pred = [0,0,0,0,1,1,1,1]print("Valor para una predicción que nunca acierta=",matthews_corrcoef(y_true,y_pred)) |
Valor para una predicción que acierta siempre= 1.0 Valor para una predicción que acierta la mitad= 0.0 Valor para una predicción que nunca acierta= -1.0
La métrica también está en tfa.metrics.MatthewsCorrelationCoefficient pero
he visto que no tiene el parámetro
threshold por lo que supongo que solo trabaja con valores de predicción y no de score.
Además en https://stackoverflow.com/questions/56865344/how-do-i-calculate-the-matthews-correlation-coefficient-in-tensorflow se indica que:
Also please note that MCC values printed from Keras during iterations will be incorrect because of the metric calculation per batch size. You can only trust MCC value from calling "evaluate" or "score" after fitting. This is because MCC for the whole sample is not the sum/average of the parts, unlike the other metrics. For example, if your batch size is one, MCC printed will be zero during iterations.
Mas información:
clase/iabd/pia/2eval/tema07-apendices-metricas.1710010230.txt.gz · Última modificación: 2024/03/09 19:50 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3