Herramientas de usuario
−Barra lateral
−Tabla de Contenidos
3. NumPy
Nunpy es una librería para facilitar el manejo de vectores, matrices o tensores. Un tensor es como una matriz pero con mas de 2 dimensiones. Una de sus mayores utilidades es lo rápido que hace las operaciones ya que los paraleliza siempre que puede.
Para ver lo rápido que funciona numpy, veamos un ejemplo en el que se multiplican todos los elementos de un array y se suman el resultado
1 2 3 4 5 6 7 8 |
import numpy as npfrom time import perf_counternp.random.seed(5)array_size = 10000000array1 = np.random.rand(1,array_size)array2 = np.random.rand(1,array_size) |
1 2 3 4 5 6 7 |
t1 = perf_counter()resultado = 0for i in range(array1.shape[1]): resultado +=array1[0,i]*array2[0,i]t2 = perf_counter()print("Resultado = " + str(resultado))print("Tiempo = " + str(t2 - t1) + " s") |
Resultado = 2499423.5030155224 Tiempo = 5.321726399999989 s
1 2 3 4 5 |
t1 = perf_counter()resultado = np.dot(array1,array2.T)t2 = perf_counter()print("Resultado = " + str(resultado[0][0]))print("Tiempo = " + str(t2 - t1) + " s") |
Resultado = 2499423.5030155387 Tiempo = 0.011971984000069824 s
Usando un array se tarda 5,3 segundos mientras que usando numpy se arda solo 0,012 segundos. La diferencia es abismal.
Mas información:
Instalación e importación
Instalación
- Instalación con conda
1 |
conda install numpy |
Importación
- Importar numpy
1 |
import numpy as np |
Creación
Crear un array
- Crea el array copiando los datos que le pasamos por parámetro
1 |
a=np.array([10,20,30,40,50]) |
asarray y en este caso si puede no se copia el array.
- Indicando el tipo
1 |
a=np.array([10,20,30,40,50],dtype=np.int32) |
Los tipos de datos que soporta NumPy son los siguientes: NumPy Data Types
Crear un rango de valores
- Desde un valor inicial , el valor final y los incrementos desde el valor inicial. Es similar a la función de python
range
1 |
a=np.arange(100,200,10) |
array([100, 110, 120, 130, 140, 150, 160, 170, 180, 190])
np.arange y range es que range solo permite valores enteros:
np.arange(0.1,2.5,0.2)
range(1,3,1)
arange no obtiene el último valor. En el ejemplo es 200
- Crear un conjunto de datos linealmente equidistantes. Se indica el valor inicial , el final y cuantos valores queremos.
1 |
a=np.linspace(0,5,20) |
array([0. , 0.26315789, 0.52631579, 0.78947368, 1.05263158,
1.31578947, 1.57894737, 1.84210526, 2.10526316, 2.36842105,
2.63157895, 2.89473684, 3.15789474, 3.42105263, 3.68421053,
3.94736842, 4.21052632, 4.47368421, 4.73684211, 5. ])
linspace si obtiene el último valor. En el ejemplo es 5
Mas información:
Crear una matriz
(102304607)
1 |
a=np.array([[10,2],[30,4],[60,7]]) |
Acceso a datos
Para acceder a filas (o columnas, etc) se usan los corchetes []
Se puede acceder de las siguientes formas:
[4]: Nº de fila[ [4,7] ]: Un array con varios números de fila[:]: Todas las filas.[3:7]: Un rango de filas[ [True,False,True,True] ]: Un array del mismo tamaño que el Nº de filas indicando que filas se retornan
Si los números son negativos se empieza por el final
[-1]: Última fila[ [-1,-2] ]: Un array con varios números de fila que son la última y la penúltima[ [3,-2] ]: Un array con varios números de fila que son la 4º fila y la penúltima[1:-2]: Desde la 2º Fila a la penúltima fila
Ejemplos:
(102304607)
- Todas las filas de la columna 0
1 2 |
a=np.array([[10,2],[30,4],[60,7]])a[:,0] |
array([10, 30, 60])
- Todas las filas de la columna última
1 2 |
a=np.array([[10,2],[30,4],[60,7]])a[:,-1] |
array([2, 4, 7])
- Todas las columnas de la fila 0
1 2 |
a=np.array([[10,2],[30,4],[60,7]])a[0,:] |
array([10, 2])
- Todas las columnas de la última fila
1 2 |
a=np.array([[10,2],[30,4],[60,7]])a[-1,:] |
array([60, 7])
(1029.53041.66078.2)
- Todas las filas y las columnas segunda y tercera
1 2 |
a=np.array([[10,2,9.5],[30,7,1.6],[60,4,8.2]])a[:,[1,2]] |
array([[2. , 9.5],
[7. , 1.6],
[4. , 8.2]])
- Todas las columnas y las filas segunda y tercera
1 2 |
a=np.array([[10,2,9.5],[30,7,1.6],[60,4,8.2]])a[[1,2],:] |
array([[30. , 7. , 1.6],
[60. , 4. , 8.2]])
Acceso mediante booleanos
Acceso mediante booleanos
1 2 |
a=np.array([1,2,3,4,5])a[ [False, False, False, True, True] ] |
array([4, 5])
Pero esa forma de acceder permite hacer un truco que explicamos a continuación.
- Muestra un array de booleanos de los datos que son mayores de 3
1 2 3 |
a=np.array([1,2,3,4,5])b=a>3b |
array([False, False, False, True, True])
Y ahora podemos usar el array b para buscar los elementos de a.
1 |
a[b] |
array([4, 5])
Pero se puede hacer de forma simplificada de la siguiente forma:
- Mostrar los que sean mayores de 3
1 2 |
a=np.array([1,2,3,4,5])a[a>3] |
array([4, 5])
- Mostrar lo que sean mayores que 3 o menores que 2
1 2 |
a=np.array([1,2,3,4,5])a[(a>3) | (a<2)] |
array([1, 4, 5])
a[ [0,3],:] o a[:,[0,3] ] pero lo que no podemos es hacerlo a la vez.
(12345678910111213141516)
El siguiente código:
1 2 3 |
a=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])a[[0,2],[2,3]] |
Muestra ésto:
[ 2 12]
¿De donde salen esos valores? Porque son lista de filas y columnas. Es decir que realmente quieres los puntos (0,1) y (2,3) que corresponden a los valores 2 y 12. Es decir que está indicando listas de puntos pero el primer parámetro son las filas y en el segundo parámetro son las columnas.
¿entonces como podemos hacer lo que queríamos hacer de obtener la 2 filas y las 2 columnas? Generando primero la matriz con las filas que queremos y luego obteniendo las columnas que queremos.
1 2 |
a=np.array([[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]])a[[0,2],:][:,[1,3]] |
1 2 |
[[ 2 4] [10 12]] |
Operaciones
Modificar con operaciones
- Multiplicar una matriz por un escalar
1 2 |
a=np.array([[10,20],[30,40],[60,70]])np.multiply(a,2) |
array([[ 20, 40],
[ 60, 80],
[120, 140]])
- Multiplicar una matriz por otra
1 2 3 |
a=np.array([[10,20],[30,40],[60,70]])b=np.array([[2,3],[5,7],[11,13]])np.multiply(a,b) |
array([[ 20, 60],
[150, 280],
[660, 910]])
- Varias operaciones. En este ejemplo se multiplica por 3, se le suma 7 y se divide entre 9.
1 2 |
a=np.array([[10,20],[30,40],[60,70]])np.divide(np.add(np.multiply(a,3),7),9) |
array([[ 4.11111111, 7.44444444],
[10.77777778, 14.11111111],
[20.77777778, 24.11111111]])
- Varias operaciones. En este ejemplo se multiplica por 3, se le suma 7 y se divide entre 9. Pero se usa la sobrecarga de operadores.
1 2 |
a=np.array([[10,20],[30,40],[60,70]])(a*3+7)/9 |
array([[ 4.11111111, 7.44444444],
[10.77777778, 14.11111111],
[20.77777778, 24.11111111]])
- Multiplicación de matrices
1 2 3 |
a=np.array([[10,20]])b=np.array([[2],[30]])np.matmul(a,b) |
array([[620]])
- Multiplicación de matrices.Pero se usa la sobrecarga de operadores.
1 2 3 |
a=np.array([[10,20]])b=np.array([[2],[30]])a@b |
array([[620]])
@.
Aplicar función
Aplicar una función a todos los elementos de un array
1 2 3 |
a=np.array([10,20,30,40,50])f=lambda x: x+5np.array([f(x) for x in a]) |
array([15, 25, 35, 45, 55])
multiply o add
Añadir elementos con append
Para añadir filas o columnas se usa append. El parámetro axis indica en que eje se añade, filas, columnas, etc.
(123102030100200300)
- Se añaden filas con
axis=0
1 2 3 |
a=np.array([[1,2,3],[10,20,30],[100,200,300]])a=np.append(a,[[1000,2000,3000]], axis=0)a |
array([[ 1, 2, 3],
[ 10, 20, 30],
[ 100, 200, 300],
[1000, 2000, 3000]])
- Se añaden columnas con
axis=1
1 2 3 |
a=np.array([[1,2,3],[10,20,30],[100,200,300]])a=np.append(a,[[4],[40],[400]], axis=1)a |
array([[ 1, 2, 3, 4],
[ 10, 20, 30, 40],
[100, 200, 300, 400]])
[ [4],[40],[400] ]
Información
(1029.53041.66078.2)
Máximo de un array
- De todo el tensor
1 2 |
a=np.array([[10,2,9.5],[30,7,1.6],[60,4,8.2]])np.max(a) |
60
- Del Eje 0. Es decir, el máximo de cada columna
1 2 |
a=np.array([[10,2,9.5],[30,7,1.6],[60,4,8.2]])np.max(a,axis=0) |
array([60. , 7. , 9.5])
- Del eje 1. Es decir, el máximo de cada fila
1 2 |
a=np.array([[10,2,9.5],[30,7,1.6],[60,4,8.2]])np.max(a,axis=1) |
array([10., 30., 60.])
Índice del máximo
- De todo el array
1 2 |
a=np.array([10,20,200,40,50])np.argmax(a) |
2
Valores únicos
1 |
np.unique([1,2,2,3,2,1,2,3,1,2]) |
array([1, 2, 3])
Dimensiones
1 2 |
a=np.array([10,20,30,40,50])a.ndim |
1
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.ndim |
2
Forma del tensor
1 2 |
a=np.array([10,20,30,40,50])a.shape |
(5,)
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.shape |
(3,2)
Tipo de datos
* Obtener el tipo de datos de un tensor
1 2 |
a=np.array([10,20,30,40,50])a.dtype |
dtype('int64')
Memoria
* Obtener cuanta memoria usa un array de int32
1 2 |
a=np.array([10,20,30,40,50],dtype=np.int32)a.nbytes |
20
* Obtener cuanta memoria usa un array de int64
1 2 |
a=np.array([10,20,30,40,50],dtype=np.int64)a.nbytes |
40
* Obtener cuanta memoria usa un array con el tipo por defecto
1 2 |
a=np.array([10,20,30,40,50])a.nbytes |
40
Transformaciones
Tipos de datos
- Transformar a un número entre 0 y 255 sin signo
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.astype(np.uint8) |
- Transformar a un número en coma flotante de 64 bits
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.astype(np.float64) |
Los tipos de datos que soporta NumPy son los siguientes: NumPy Data Types
Unir tensores
- Añadir elementos a un vector
1 2 3 4 |
a=[1,2,3,4]b=[10,11,12]np.append(a,b) |
array([ 1, 2, 3, 4, 10, 11, 12])
- Concatenar columnas
unir(103060)con(247)
1 2 3 |
a=np.array([10, 30, 60])b=np.array([2,4,7])np.column_stack((a,b)) |
array([[10, 2],
[30, 4],
[60, 7]])
(102304607)
column_stack y append ya que ambas pueden hacer lo mismo pero con append es más complejo
1 2 3 |
a=np.array([10, 30, 60])b=np.array([2,4,7])np.append(a.reshape(-1,1),b.reshape(-1,1),axis=1) |
array([[10, 2],
[30, 4],
[60, 7]])
Transformar de matriz a array
- Indicando el tamaño del array
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.reshape(6) |
array([10, 20, 30, 40, 60, 70])
- Si se pasa como argumento el
-1, numpy calcula el tamaño automáticamente.
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.reshape(-1) |
array([10, 20, 30, 40, 60, 70])
Transformar de array a matriz
- Transformar indicando exactamente el tamaño de la matriz (2,3)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(2,3)) |
array([[10, 20, 30],
[40, 60, 70]])
- Transformar indicando exactamente el tamaño de la matriz (3,2)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(3,2)) |
array([[10, 20],
[30, 40],
[60, 70]])
- Transformar pero sin indicar el tamaño de una de las dimensiones (2,-1)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(2,-1)) |
array([[10, 20, 30],
[40, 60, 70]])
- Transformar pero sin indicar el tamaño de una de las dimensiones (3,-1)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(3,-1)) |
array([[10, 20],
[30, 40],
[60, 70]])
- Transformar pero sin indicar el tamaño de una de las dimensiones (-1,2)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(-1,2)) |
array([[10, 20],
[30, 40],
[60, 70]])
- Transformar pero sin indicar el tamaño de una de las dimensiones (-1,3)
1 2 |
a=np.array([10, 20, 30, 40, 60, 70])np.reshape(a,(-1,3)) |
array([[10, 20, 30],
[40, 60, 70]])
Transformar de array a array
- Cambiar de fila a columna
1 |
np.array([1,2,3,4,5]).reshape(-1,1) |
array([[1],
[2],
[3],
[4],
[5]])
Transformar de matriz a matriz
- Transformar de una matriz de (3,2) a (2,3)
1 2 |
a=np.array([[10,20],[30,40],[60,70]])np.reshape(a,(2,3)) |
array([[10, 20, 30],
[40, 60, 70]])
- Transformar de una matriz de (3,2) pero sin indicar el tamaño de una de las dimensiones (-1,3)
1 2 |
a=np.array([[10,20],[30,40],[60,70]])np.reshape(a,(-1,3)) |
array([[10, 20, 30],
[40, 60, 70]])
- Calcula la matriz transpuesta.
1 2 |
a=np.array([[10,20],[30,40],[60,70]])a.T |
array([[10, 30, 60],
[20, 40, 70]])
Meshgrid
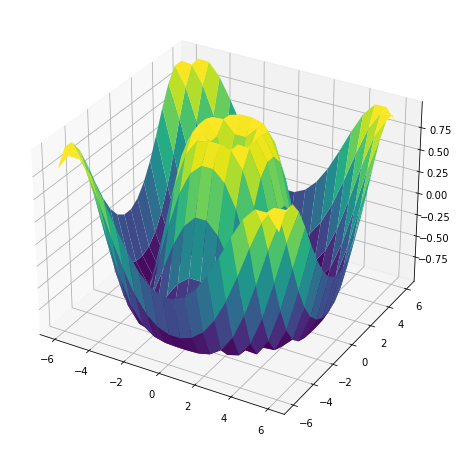
Dados dos vectores, hace una combinación de ambos vectores. Se usa sobre todo para crear gráficos en 3D.
- En
xeyal aplicarmeshgridtenemos la combinación de todos ellos. Y enzlos valores de cada punto.
1 2 3 4 5 |
import numpy as npx=np.linspace(-6,6,20)y=np.linspace(-6,6,20)x,y=np.meshgrid(x,y)z=np.sin(np.sqrt(x ** 2 + y ** 2)) |
La z es la siguiente fórmula:
z=sin(√x2+y2)
- Ahora mostramos el gráfico de
x,yyz.
1 2 3 4 5 |
import matplotlib.pyplot as pltfigure=plt.figure(figsize=(15, 8))axes = figure.add_subplot(projection='3d')axes.plot_surface(x,y,z,cmap='viridis') |
Imprimir
Se puede imprimir un array de numpy con la función print pero a veces queremos que no salga la notación científica y para ello usaremos:np.set_printoptions(suppress = True)
1 2 |
a=np.array([0.000010,0.000020,0.000030,0.000040,0.000050])print(a) |
[1.e-05 2.e-05 3.e-05 4.e-05 5.e-05]
Pero si ejecutamos la orden np.set_printoptions(suppress = True)
1 2 3 |
np.set_printoptions(suppress = True)a=np.array([0.000010,0.000020,0.000030,0.000040,0.000050])print(a) |
[0.00001 0.00002 0.00003 0.00004 0.00005]
Otro problema es que si hay muchas columnas a filas , no se muestra todo al imprimirlo.
1 2 |
a=np.zeros((32,32))print(a) |
[[0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] ... [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.] [0. 0. 0. ... 0. 0. 0.]]
Para hacer que se muestre toda la matriz se puede hacer con np.set_printoptions(threshold=np.inf)
Mas información:
Guardar y cargar
- Para guardar un tensor como un fichero de texto se usa el método
savetxt
1 2 |
a=np.array([[10,20],[30,40],[60,70]])np.savetxt("datos.csv",a,delimiter=",") |
- Para cargar un fichero se usa el método
genfromtxt
1 2 |
b=np.genfromtxt("datos.csv",delimiter=",")b |
array([[10., 20.],
[30., 40.],
[60., 70.]])
También podemos guardar estructuras más complejas como mapas con np.save:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import numpy as npdatos=np.array([ { "a":[1,2,3,4], "b":[10,20,30,40] },{ "a":[1.2,2.2,3.2,4.2], "b":[10.2,20.2,30.2,40.2] },{ "a":[1.3,2.3,3.3,4.3], "b":[10.3,20.3,30.3,40.3] }])print(datos)print(datos[2]["a"])np.save("datos.npy",datos) |
[{'a': [1, 2, 3, 4], 'b': [10, 20, 30, 40]}
{'a': [1.2, 2.2, 3.2, 4.2], 'b': [10.2, 20.2, 30.2, 40.2]}
{'a': [1.3, 2.3, 3.3, 4.3], 'b': [10.3, 20.3, 30.3, 40.3]}]
[1.3, 2.3, 3.3, 4.3]
y volver a leerlas con np.load:
1 2 3 |
nuevos_datos=np.load("datos.npy",allow_pickle=True)print(nuevos_datos)print(nuevos_datos[2]["a"]) |
[{'a': [1, 2, 3, 4], 'b': [10, 20, 30, 40]}
{'a': [1.2, 2.2, 3.2, 4.2], 'b': [10.2, 20.2, 30.2, 40.2]}
{'a': [1.3, 2.3, 3.3, 4.3], 'b': [10.3, 20.3, 30.3, 40.3]}]
[1.3, 2.3, 3.3, 4.3]
allow_pickle=True se usa para indicar que se puedan cargar objetos desde el fichero. Eso tiene riesgos de seguridad pero en nuestro entorno no suele ser un problema ya que suelen ser datos guardados por nosotros.
Ejercicios
Ejercicio 1
Crea una array de numpy con los siguiente números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
- Muestra el último elemento. Y debes hacerlo sin saber su longitud.
- Muestra el 3º elemento
- Muestra el último y 3º elemento.
- Muestra del 2º al 5º elemento.
- Muestra el 2° y el 5° elemento
- Muestra el último y el penúltimo elemento. Y debes hacerlo sin saber su longitud.
Ejercicio 2: arange
- Crea una array de numpy con los siguiente números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 pero que el array sea de tipo "float" de 32 bits.
- Usando la función
arangede numpy crea un array con los números del 100 al 200 pero sin incluir el 200. Muestra el resultado. - Usando la función
rangeestándar de Python crea un array con los números del 100 al 200 pero sin incluir el 200. Muestra el resultado. ¿Que diferencia hay conarange?
Ejercicio 3: Matrices
- Crea la siguiente matriz:
(1465417329126311)
- Muestra el elemento de la fila 2º y la columna 3º. Es el valor del 7.
- Muestra la 3º Fila
- Muestra la 2º Columna
- Muestra la 2º y 3º Columna
- Muestra la 2º y 3º Fila
- Muestra la última columna. Debe funcionar independientemente del número de columnas.
- Muestra la 2º y 4º Columna y la 1º y 3º fila
- Muestra de la 2º a la 3º Columna y de la 1º a la 3º fila
- Muestra todas las columnas excepto la primera y la última. Debe funcionar independientemente del número de columnas.
- Muestra todas las filas excepto la primera y la última. Debe funcionar independientemente del número de filas.
- Muestra todas las columnas excepto la primera y la última y todas las filas excepto la primera y la última. Debe funcionar independientemente del número de filas y columnas.
- Imprime la matriz y haz que las cabeceras de cada columna sean A, B , C y D
Ejercicio 4: Filtrado
El siguiente array contiene las temperaturas medias que ha hecho en Valencia en cada mes [10.2, 10.7, 13.3, 15.8, 19.3, 23.6, 26, 25.9, 22.8, 19.1, 13.9, 10.8 ]
- Muestra las temperaturas cuyo valor sea mayor que 20
- Muestra las temperaturas cuyo valor sea menor que 11
- Muestra las temperaturas cuyo valor sea mayor que 20 o menor que 11
Ejercicio 5: Matrices e Iris
Carga los datos del ejemplo de las flores con el siguiente código:
1 2 3 |
from sklearn.datasets import load_irisdatos=load_iris().dataresultado=load_iris().target |
- Crea un array llamado
sepal_lengthcon las 99 primeras filas y la 1º columna de la matrizdatos - Crea un array llamado
petal_lengthcon las 99 primeras filas y la 3º columna de la matrizdatos - Crea un array llamado
xjuntando las 2 columnassepal_lengthypetal_length - Crea un array llamado
ycon las 99 primeras filas del vectorresultado
Ejercicio 6: Matrices e Iris
Carga los datos del ejemplo de las flores con el siguiente código:
1 2 3 |
from sklearn.datasets import load_irisdatos=load_iris().dataresultado=load_iris().target |
- Crea un array llamado
xcon las 99 primeras filas , la 1º columna y la 3º columna de la matrizdatos - Crea un array llamado
ycon las 99 primeras filas del vectorresultado
Ejercicio 7: Matrices 2D
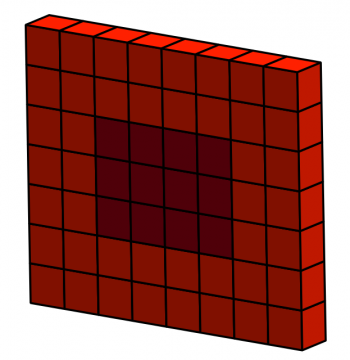
Ejercicio 8: Matrices 3D
Selecciona las celdas en rojo oscuro de la siguiente matriz:
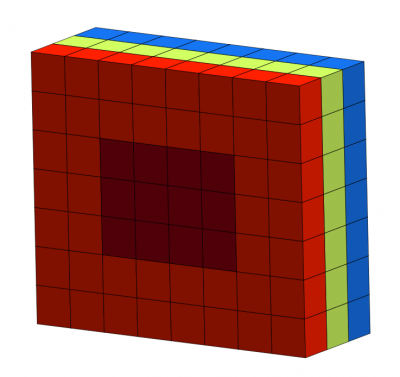
Ahora selecciona las celdas en rojo oscuro pero también las verdes y azules que hay por detrás de las rojo oscuro.
Ejercicio 9: Matrices
- Crea la siguiente matriz:
(1465417329126311)
- A todos los elementos de la matriz sumale un 10. Usando las funciones de numpy
- A todos los elementos de la matriz sumale un 10 y divídelos entre 2. Usando las funciones de numpy
- A todos los elementos de la matriz sumale un 10. Usando operadores
- A todos los elementos de la matriz sumale un 10 y divídelos entre 2. Usando operadores
Ejercicio 10: Matrices
- Crea la siguiente matriz:
(123456789)
- Multiplica cada elemento de la matriz por si mismo
- Multiplica la matriz por si misma
Ejercicio 11: Funciones a arrays
Crea una función llamada f que acepte como parámetro el número y que retorne el valor multiplicado por 2 y además que se le sume 1.
Crea ahora el vector de numpy [1,5,4,7,3,9,8,6] y aplícale la función f
Ejercicio 12: Funciones a arrays
Crea una función llamada f que acepte como parámetro el número y que retorne lo siguiente:
- Si es valor está en el rango ]-inf,3[ que retorne 0
- Si es valor está en el rango [3,5[ que retorne 4
- Si es valor está en el rango [5,6[ que retorne 5
- Si es valor está en el rango [6,7[ que retorne 6
- Si es valor está en el rango [7,9[ que retorne 8
- Si es valor está en el rango [9,+inf[ que retorne 10
Crea ahora el vector de numpy [1,5,4,7,3,9,8,6] y aplícale la función f
Ejercicio 13: Máximos
En el tema anterior creamos un array con las neuronas de cada capa para cada red en el problema del cáncer de mama.
1 |
redes=[[4, 8, 4, 2, 1], [4, 8, 4, 2, 1], [8, 16, 8, 4, 1], [8, 16, 8, 4, 1], [16, 32, 16, 8, 1], [16, 32, 16, 8, 1], [32, 64, 32, 8, 1], [32, 64, 32, 8, 1], [64, 128, 64, 8, 1], [64, 128, 64, 8, 1]] |
Calcula:
- El Nº Máximo de neuronas de una capa que llegó a haber en cualquier red
- El Nº máximo de neuronas que hubo en cada red
- El Nº máximo de neuronas que hubo en cada capa
- El Nº máximo de neuronas que hubo en la 3º red
- El Nº máximo de neuronas que hubo en la 3º capa
Ejercicio 14:Únicos
Obtén los posibles valores de tipos de flor del tema 1. Es decir mostrar los valores único de la y
Y lo mismo con el problema del cáncer de mama
Ejercicio 15:Dimensiones
Muestra con numpy el número de dimensiones de los siguientes arrays:
1 |
a=[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] |
1 |
b=[[2, 3], [5, 7], [11, 13], [17, 19], [23, 29], [31, 37]] |
1 |
c=[[[2, 3], [5, 7]], [[11, 13], [17, 19]], [[23, 29], [31, 37]]] |
Ejercicio 16:Forma
Crea una función llamada mostrar_tamanyo que le pasemos un array de numpy y nos imprima el tamaño de cada una de las dimensiones.
Por ejemplo con el array [ [ [2, 3], [5, 7]], [ [11, 13], [17, 19]], [ [23, 29], [31, 37] ] ] deberá mostrar
El nº de elementos de la dimension 0 es 3 El nº de elementos de la dimension 1 es 2 El nº de elementos de la dimension 2 es 2
Prueba tambien con los siguientes arrays
1 |
a=[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37] |
1 |
b=[[2, 3], [5, 7], [11, 13], [17, 19], [23, 29], [31, 37]] |
1 |
c=[[[2, 3], [5, 7]], [[11, 13], [17, 19]], [[23, 29], [31, 37]]] |
Ejercicio 17:Tipo de datos
Muestra con numpy el tipo de datos de los siguientes arrays:
1 |
a=[2, 3, 5] |
1 |
b=[2.4, 3.2, 5.6] |
1 |
c=[2, 3, 5.6] |
Ejercicio 18:Transformar tipos de datos
- Transforma el siguiente array en 8 bits sin signo y muestra cuanto ocupa en memoria
1 |
a=np.array([1, -2, 3]) |
- Transforma el siguiente array en 8 bits sin signo y muestra cuanto ocupa en memoria
1 |
b=np.array([1,254,255]) |
- Transforma el siguiente array en 8 bits con signo y muestra cuanto ocupa en memoria
1 |
b=np.array([1,127,128]) |
- Transforma el siguiente array en 8 bits con signo y muestra cuanto ocupa en memoria
1 |
b=np.array([1,-128,-129]) |
- Transforma el siguiente array en float32 y muestra cuanto ocupa en memoria
1 |
b=np.array([1,2,3]) |
- Transforma el siguiente array en int32 y muestra cuanto ocupa en memoria
1 |
b=np.array([1.9,2.01,3.51]) |
Ejercicio 19: Unir columnas
En ejercicios anteriores obtuviste para el problema de las flores , una matriz x y un vector y.
Une los datos en una nueva matriz de forma que cada fila de la nueva matriz contenga los datos de cada fila de la x y el dato correspondiente de la y.
Y lo mismo con el problema del cáncer de mama
Ejercicio 20: Transformar tensores
El fichero mario.csv que hay dentro de mario.zip contiene un array de numpy. Este array corresponde a la siguiente imagen que tiene el tamaño 41x31:
- Carga el array desde disco y llámalo
mario. - Muestra el tamaño de sus dimensiones usando la función que creaste en un ejercicio anterior.
- Muestra la imagen con el siguiente código. No te dejará. ¿Por qué?
1 2 3 4 |
import matplotlib.pyplot as pltfigure=plt.figure()axes = figure.add_subplot()axes.imshow(mario) |
- Transforma el array a otro cuyo tamaño sea 41x31 y que la última dimensión no se indique. ¿Cual es el tamaño de la última dimensión?
- ¿cual es el tipo? ¿Cuanto ocupa en memoria?
- Muestra otra vez la imagen. No te dejará. ¿Por qué?
- Transforma la matriz en 8 bits sin signo.¿Cuanto ocupa ahora en memoria?
- Muestra otra vez la imagen. Ahora si que te dejará. ¿Por qué?
- Muestra ahora los datos de la matriz del color Rojo.
- Muestra ahora los datos de la matriz del color Verde.
- Muestra ahora los datos de la matriz del color Azul.
- Muestra los colores RGB del pixel (2,3)
- Obtén los datos de la matriz del color Rojo, aplica su transpuesta y muestra la imagen.
- Divide todos los valores del tensor entre 2 y muestra la imagen.
Ejercicio 21: Transformar tensores
Siguiente con el tensor del ejercicio anterior de mario. Aplica a todos los elementos la siguiente función:
- Si el valor está entre
[0,63]se transformará en 0 - Si el valor está entre
[64,127]se transformará en 90 - Si el valor está entre
[128,191]se transformará en 150 - Si el valor está entre
[192,255]se transformará en 200
Para hacerlo deberás transformar el tensor otra vez en un array unidimensional, aplicar la función y volver a transformarlo en un tensor de 3 dimensiones
Ejercicio 22: linspace y gráficas
Dado el siguiente código python:
1 2 3 4 5 6 7 8 9 10 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize=(8,8))axes = figure.add_subplot() x=[-3,-2,-1,0,1,2,3]y = 3*(1 - x)**2 * np.exp(-x**2 ) - 10*(x/5 - x**3 )*np.exp(-x**2 ) - 1./3*np.exp(-(x + 1)**2 ) axes.plot(x,y) |
- Modifica el código que genera la variable
xpara que sea un array de numpy y de tipofloat. Muestra la imagen - Modifica el código que genera la variable
xpara que sean 10 valores entre el [-3,3]. Muestra la imagen - Modifica el código que genera la variable
xpara que sean 20 valores entre el [-3,3]. Muestra la imagen - Modifica el código que genera la variable
xpara que sean 40 valores entre el [-3,3]. Muestra la imagen - Modifica el código que genera la variable
xpara que sean 60 valores entre el [-3,3]. Muestra la imagen - Modifica el código que genera la variable
xpara que sean 100 valores entre el [-3,3]. Muestra la imagen
Ejercicio 23: El vino
Cargas con numpy el fichero wine.csv que contiene una matriz de números separados por coma.
La matriz contiene una serie de columnas con características del vino y la última columna indica el tipo del vino.
- Crea una función en python llamada
imprimir_datosy tendrá como parámetro una matriz de numpy de forma que:- Imprima cuantas características tenemos de cada tipo de vino.
- Imprima cuantas muestra de vino tenemos
- Imprima cuantos tipos distintos de vino tenemos y cuales son
- Imprima los valores máximos y mínimos de cada característica
- Retorna una nueva matriz llamada
xsolo con las características y un nuevo array llamadoysolo con los tipos de vino
- Llama a la función
imprimir_datoscon los datos dewine.csv
Ejercicio 24: Función de pérdida
El método fit que entrena la red neuronal, retorna un objeto history que nos ayuda a obtener el valor de la función de pérdida.
1 |
history=model.fit(x, y,epochs=40) |
Del objeto history podemos obtener un array con el valor de la función de pérdida en cada una de las épocas de entrenamiento:
1 |
loss=history.history['loss'] |
Por lo tanto loss[0] no dirá el valor de la función de pérdida después de acabar la primera época.
Vuelve a ejecutar el código de la primera red neuronal del curso pero ahora imprime el valor de la función de pérdida tras la última época de entrenamiento.
Ejercicio 25: Función de pérdida
Repite el ejercicio del tema anterior de la forma de la flor pero ahora cambia el resultado de la tabla:
Nº Red Épocas loss Mitad loss Final Tiempo (s) ---- ------------- -------- ------------ ------------ ------------ 0 4,8,4,2,1 20 0.209651 0.191906 0.79 1 4,8,4,2,1 40 0.189802 0.111734 0.86 2 8,16,8,4,1 20 0.218724 0.190873 0.73 3 8,16,8,4,1 40 0.187368 0.131706 0.87 4 16,32,16,8,1 20 0.143569 0.0653756 0.72 5 16,32,16,8,1 40 0.0548877 0.0046529 0.87 6 32,64,32,8,1 20 0.0211689 0.00260244 0.74 7 32,64,32,8,1 40 0.00226261 7.84583e-05 0.87 8 64,128,64,8,1 20 0.0129097 0.00143349 0.77 9 64,128,64,8,1 40 0.00150978 8.06734e-05 1.16
Es decir que en vez de mostrar el Result 1 y Result 2 muestra el resultado de la función de pérdida a mitad de entrenamiento (Nº de épocas/2) y al final del entrenamiento
Ejercicio 26: Derivadas
Crea las siguiente funciones:
- Crea una función llamada
resta_siguienteque acepte como parámetro un array llamadoa. Esta función hará lo siguiente:- Crea un array llamado
primerosque contenga todos los elementos del array menos el último - Crea un array llamado
ultimosque contenga todos los elementos del array menos el primero - Retorna el resultado de restar
ultimosmenosprimeros
- Crea una función llamada
derivadaque acepte como parámetro dos arrays llamadosxyy.- Crea un array llamado
resta_xque sea el resultado de llamar a la funciónresta_siguientecon el argumentx - Crea un array llamado
resta_yque sea el resultado de llamar a la funciónresta_siguientecon el argumenty - Retorna dos valores que serán:
- El array
xmenos el último elemento - El resultado de dividir
resta_yentreresta_x
Con todo ello haz el siguiente programa:
- Crea un array llamado
x, con 100 números entre el -2 y el 2 - Crea un array llamado
y_absolutoque sea el valor absoluto del arrayx - Crea un array llamado
y_cuadradoque sea el valor al cuadrado del arrayx - Llama a la función
derivadacon los argumentosxey_absolutoy guarda el resultado en los arraysderivada_x_absoluto,derivada_y_absoluto - Llama a la función
derivadacon los argumentosxey_cuadradoy guarda el resultado en los arraysderivada_x_cuadrado,derivada_y_cuadrado
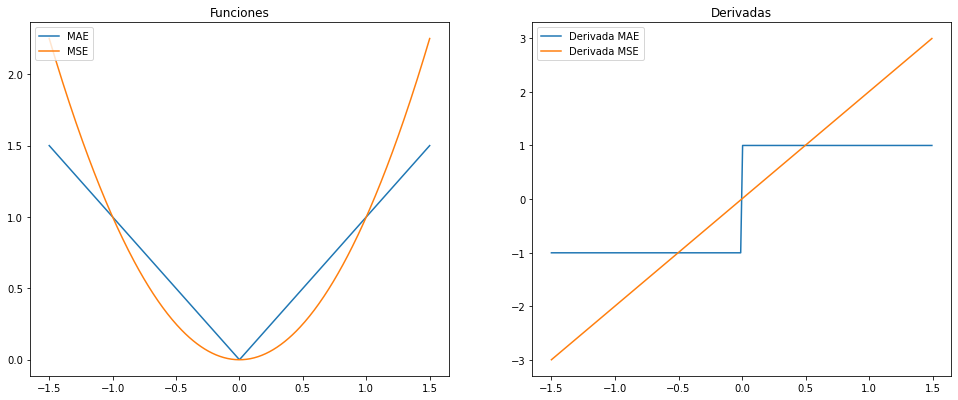
Muestra el resultado de todos los arrays con el siguiente código:
1 2 3 4 5 6 7 8 9 10 11 12 |
import matplotlib.pyplot as plt figure=plt.figure(figsize=(16,8))axes = figure.add_subplot(1,2,1)axes.plot(x,y_absoluto,label="Absoluto")axes.plot(x,y_cuadrado,label="Cuadrado")axes.legend(loc="upper left")axes = figure.add_subplot(1,2,2)axes.plot(derivada_x_absoluto,derivada_y_absoluto,label="Derivada Absoluto")axes.plot(derivada_x_cuadrado,derivada_y_cuadrado,label="Derivada Cuadrado")axes.legend(loc="upper left") |
La imagen resultante debe ser similar a ésta:
Mini-proyecto
Paso 1
De varios paises tenemos los siguientes datos del gatos en educación y su PIB.
| Gasto en educación (Miles de millones de €) | PIB (Miles de millones de €) |
|---|---|
| 2,016 | 56,180 |
| 4,797 | 47,188 |
| 9,237 | 57,689 |
| 14,115 | 43,703 |
| 14,926 | 59,102 |
| 17,344 | 65,960 |
| 17,624 | 45,743 |
| 22,418 | 13,575 |
| 25,313 | 68,437 |
| 34,858 | 147,153 |
| 38,874 | 25,396 |
| 42,013 | 74,390 |
| 46,635 | 98,933 |
| 49,585 | 116,070 |
| 50,183 | 138,555 |
| 52,066 | 139,366 |
| 54,688 | 150,096 |
| 57,130 | 156,143 |
| 66,356 | 119,758 |
| 69,054 | 139,081 |
| 69,512 | 128,722 |
| 69,837 | 152,651 |
| 79,766 | 148,231 |
| 81,837 | 137,863 |
| 87,098 | 217,289 |
| 89,004 | 168,649 |
| 93,171 | 163,105 |
| 93,660 | 200,476 |
| 94,194 | 150,440 |
| 97,369 | 173,205 |
Con esos datos vamos a entrenar redes neuronales para que en base al gasto en educación podamos averiguar el PIB del país.
La siguiente función get_datos() nos retorna los datos en una matriz:
1 2 3 4 5 6 7 8 9 10 11 12 |
def get_datos(): datos= [[ 2.01666708 , 56.18031474], [ 4.79734083 , 47.18848199], [ 9.23784581 , 57.68974048], [ 14.11529384 , 43.70348368], [ 14.92688637 , 59.10244323], [ 17.34408196 , 65.96080804], [ 17.62435324 , 45.74334603], [ 22.41875021 , 13.575581 ], [ 25.3139145 , 68.43756969], [ 34.85886672 , 147.15375307], [ 38.87476262 , 25.39687009], [ 42.01380169 , 74.39010069], [ 46.63551059 , 98.93395801], [ 49.58578273 , 116.07013679], [ 50.18371003 , 138.55546747], [ 52.06630172 , 139.36601894], [ 54.68810274 , 150.09622546], [ 57.13046193 , 156.14375739], [ 66.35609935 , 119.75844452], [ 69.05499042 , 139.08155228], [ 69.51252436 , 128.72247348], [ 69.83788756 , 152.65110462], [ 79.76649746 , 148.23106977], [ 81.83730552 , 137.86314926], [ 87.09879038 , 217.28932067], [ 89.00469759 , 168.64994509], [ 93.17139213 , 163.10598352], [ 93.66070686 , 200.47638924], [ 94.1944751 , 150.44019156], [ 97.36920633 , 173.2055957 ]] return datos |
Realiza lo siguiente:
- Crea una array de numpy en base a los datos.
- Obtén una "columna" llamada
x_entrenamientocon los datos de entrada a la red neuronal - Obtén una "columna" llamada
y_entrenamientocon los datos de salida de la red neuronal
Paso 2
Usando como base el siguiente código que crea y entrena un modelo de red neuronal.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def compile_fit(capas,x,y): np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() for index,neuronas_capa in enumerate(capas): if (index==0): model.add(Dense(neuronas_capa, activation='relu',input_dim=2)) elif (index==len(capas)-1): model.add(Dense(neuronas_capa, activation='sigmoid')) else: model.add(Dense(neuronas_capa, activation='relu')) model.compile(loss='mean_squared_error') history=model.fit(x, y,epochs=5000,verbose=False) return model,history |
- Modifica la función
compile_fitpara que el número de datos de entrada a la red sea el número de columnas dex, es decir modificainput_dim - Modifica la función de activación de la última capa para que sea la función de activación
linear. - Añade un parámetros llamado
epochsque sea el número de épocas a antrenar - Crea una red neuronal y entrenala con:
- Capas: 5,10,15,10,1
- Épocas: 5000
Paso 3
Calcula el error cuadrático para los siguientes datos sabiendo que el error es la resta entre el valor verdadero y el valor predicho , y luego elevándolo al cuadrado.
x | y_true | y_pred | Error=(y_true-y_pred)² |
|---|---|---|---|
| 2,016 | 56,180 | ||
| 4,797 | 47,188 | ||
| 9,237 | 57,689 | ||
| 14,115 | 43,703 |
Para ello:
- Crea un array con los datos de entrada a predecir
[ 2.01666708, 4.79734083, 9.23784581, 14.11529384 ]de forma que sea una columna y llámalox_paso3 - Crea un array con los datos de salida verdaderos
[ 56.18031474, 47.18848199, 57.68974048, 43.70348368]de forma que sea una columna y llámaloy_true_paso3 - Usando el modelo predice las salidas predichas y llámalo
y_pred_paso3 - Resta el valor de
y_true_paso3ay_pred_paso3y elévalo al cuadrado y llámaloerror_paso3: |y_truei−y_predi|2 - Une los 4 arrays es una matriz donde cada columna sea cada uno de los arrays y llámala
resultado_paso3 - Muestra el array con la función
tabulate
Paso 4
Calcula el Error cuadrático medio o Mean Squared Error o MSE
MSE=1NN∑i=1|y_truei−y_predi|2
Este valor es la media de los errores.
Paso 5
Calcula una nueva media llamada Coeficiente de determinación o R².
Lo bueno de esta nueva media es que da un valor entre -∞ y 1. Siendo 1 si no hay error, un 0 si es malo y negativo y es malísimo
Para calcular el Coeficiente de determinación debemos hacerlo de la siguiente forma:
- Calcula la media de los valores verdaderos:
media_valores_verdaderos=1NN∑i=1y_truei
- Calcula la suma de los errores
(y_true-y_pred)²
suma_errores=N∑i=1|y_truei−y_predi|2
- Calcula la suma de los errores entre la media y el valor verdadero
(y_true-media_valores_verdaderos)²
suma_valores_media=N∑i=1|y_truei−media_valores_verdaderos|2
- Por último calcula el Coeficiente de determinación con la siguiente fórmula:
coeficiente_determinación=1−suma_erroressuma_valores_media
Paso 6
Usando el código de los pasos anteriores, crea una función llamada get_metricas_modelo(model,x,y_true) que retorne el Error cuadrático medio y el Coeficiente de determinación
Usando usa función calcula el Error cuadrático medio y el Coeficiente de determinación con todos los datos
Paso 7
- Crea una red neuronal y entrenala con la siguientes capas
20,40,80,40,20,1 - Muestra el Error cuadrático medio y el Coeficiente de determinación con todos los datos
- Indica si es mejor o peor modelo que el anterior
Paso 8
- Modifica la función para que quede de la siguiente forma:
compile_fit(capas,x,y,epochs,activation). Es decirque ahora acepte un nuevo parámetro que sea la función de activación para que no sea siemprerelu. - Crea una red neuronal y entrenala con la siguientes capas
20,40,80,40,20,1y función de activaciónselu - Muestra el Error cuadrático medio y el Coeficiente de determinación con todos los datos
- Indica si es mejor o peor modelo
Paso 9
Usando la siguiente variable que define las capas y la función de activación de una serie de redes neuronales:
1 2 3 4 5 6 7 8 9 10 11 |
redes_neuronales=[ [[5,10,3,10,1],"relu"], [[5,10,3,10,1],"selu"], [[5,10,3,10,1],"tanh"], [[20,40,80,40,20,1],"relu"], [[20,40,80,40,20,1],"selu"], [[20,40,80,40,20,1],"tanh"], [[20,40,80,160,80,40,20,1],"relu"], [[20,40,80,160,80,40,20,1],"selu"], [[20,40,80,160,80,40,20,1],"tanh"] ] |
Haz que se muestre la siguiente tabla:
Nombre Capas Épocas Activación MSE R² Tiempo
Red Entrenamiento
-------- -------------------------------- -------- ------------ -------- ----------- ---------------
1 [5, 10, 30, 10, 1] 5000 relu 699.522 0.754894 6.10154
2 [5, 10, 30, 10, 1] 5000 selu 566.064 0.801657 6.25237
3 [5, 10, 30, 10, 1] 5000 tanh 5790.5 -1.02893 6.10966
4 [20, 40, 80, 40, 20, 1] 5000 relu 564.339 0.802261 6.27882
5 [20, 40, 80, 40, 20, 1] 5000 selu 195.545 0.931483 6.34035
6 [20, 40, 80, 40, 20, 1] 5000 tanh 2869.38 -0.00540068 6.36284
7 [20, 40, 80, 160, 80, 40, 20, 1] 5000 relu 530.207 0.814221 6.67132
8 [20, 40, 80, 160, 80, 40, 20, 1] 5000 selu 141.506 0.950418 6.8306
9 [20, 40, 80, 160, 80, 40, 20, 1] 5000 tanh 2870.34 -0.00573854 6.91749
Deberás volver a modificar la función compile_fit(capas,x,y,epochs,activation) para que ahora retorne como tercer parámetro el tiempo_entrenamiento
Indica:
- Cual es la mejor red
- En general cual es la mejor y peor función de activación.
- Que redes tardan más y menos en entrenar
Paso 10
Ahora usando los siguientes datos de validación:
1 2 3 4 5 6 7 8 9 |
def get_datos_validacion(): datos_validacion=[[ 1.22140488 , 59.35315077] , [ 2.42834632 , 3.50613409] , [ 4.27529991 , 70.39938914] , [ 14.44651349 , 50.0606769 ] , [ 16.10795855 , 81.08562061] , [ 16.75024181 , 33.95365822] , [ 26.80487149 , 47.1495392 ] , [ 28.81517859 ,106.34919698] , [ 48.56698654 ,120.25398606] , [ 52.08015067 ,116.7993955 ] , [ 53.30646055 ,131.30936472] , [ 55.09968806 ,131.34281752] , [ 60.39615207 , 97.77483743] , [ 73.52487026 , 92.30645543] , [ 76.2771471 ,109.9995226 ] , [ 84.56808303 ,120.60657657] , [ 89.2700557 ,117.3687155 ] , [ 91.03720679 ,159.47376137] , [ 93.53406333 ,166.44439331] , [ 94.78103495 ,180.66942656]] return datos_validacion |
Muestra también los resultados de validación:
Nombre Capas Épocas Activación MSE R² Tiempo MSE R²
Red Entrenamiento Entrenamiento Entrenamiento Validación Validación
-------- -------------------------------- -------- ------------ --------------- --------------- --------------- ------------ ------------
1 [5, 10, 30, 10, 1] 5000 relu 699.522 0.754894 6.16381 945.903 0.525757
2 [5, 10, 30, 10, 1] 5000 selu 566.064 0.801657 6.07553 844.042 0.576827
3 [5, 10, 30, 10, 1] 5000 tanh 5790.5 -1.02893 6.0547 3639.78 -0.82486
4 [20, 40, 80, 40, 20, 1] 5000 relu 564.339 0.802261 6.17346 1008.44 0.494402
5 [20, 40, 80, 40, 20, 1] 5000 selu 195.545 0.931483 6.49106 865.301 0.566168
6 [20, 40, 80, 40, 20, 1] 5000 tanh 2869.38 -0.00540068 6.28845 2088.69 -0.0471974
7 [20, 40, 80, 160, 80, 40, 20, 1] 5000 relu 530.207 0.814221 6.70275 937.015 0.530213
8 [20, 40, 80, 160, 80, 40, 20, 1] 5000 selu 141.506 0.950418 6.77586 998.083 0.499596
9 [20, 40, 80, 160, 80, 40, 20, 1] 5000 tanh 2870.34 -0.00573854 6.77296 2086.36 -0.0460281
Indica ahora según los datos de validación:
- Cual es la mejor red y porqué crees que ahora es la mejor red al usar los datos de validación
- En general cual es la mejor y peor función de activación.
Paso 11
A modo de resumen de todo el mini projecto, vuelve a hacer el ejercicio anterior pero ahora poniendo las últimas versiones de todo el código que has usado.
Paso 12
Ahora vamos a hacer otro mini proyecto usando como base todo el código que hemos creado.
El problema a resolver es averiguar el precio,en miles de dolares, de una casa en la ciudad de Boston (target o Y). Este es un clásico problema de Machine Learning. Las características (features o X) del problema son:
- Criminalidad per cápita: Representa la tasa de criminalidad por persona en la ciudad. Un valor más alto indica una mayor tasa de criminalidad.
- Porcentaje de terrenos residenciales: Representa el porcentaje de viviendas zonificadas para parcelas de más de 25,000 pies cuadrados. Las áreas con un valor más alto de ZN tienen más zonas residenciales de bajo densidad.
- Porcentaje de terrenos no comerciales: Mide el porcentaje de área en la ciudad destinada a áreas industriales. Un valor más alto sugiere una mayor cantidad de industrias en la zona.
- Proximidad al río Charles: Es una variable binaria (0 o 1) que indica si la vivienda está cerca (1) o no cerca (0) del río Charles.
- Concentración de óxidos de nitrógeno: Representa la concentración de óxidos de nitrógeno (NO) en partes por 10 millones. Esta variable se utiliza como indicador de la calidad del aire. Valores más altos indican una mayor contaminación del aire.
- Número promedio de habitaciones: Representa el número promedio de habitaciones en las viviendas. Un valor más alto sugiere casas más grandes.
- Proporción de viviendas construidas antes de 1940: Representa el porcentaje de viviendas en la zona que fueron construidas antes de 1940. Los valores más altos indican un mayor envejecimiento de la infraestructura.
- Distancia a los centros de empleo de Boston: Es una medida ponderada de la distancia desde una ubicación hasta los centros de empleo más importantes de la ciudad de Boston. Un valor más bajo indica que la vivienda está cerca de centros laborales importantes.
- Accesibilidad a carreteras radiales: Representa la accesibilidad a las principales carreteras radiales de Boston. Un valor más alto indica una mejor conectividad con las carreteras importantes.
- Impuesto sobre la propiedad: Es el valor del impuesto a la propiedad en la ciudad, en términos de $10,000. Los valores más altos indican mayores impuestos a la propiedad.
- Proporción de estudiantes por maestro: Representa la proporción de estudiantes por cada maestro en las escuelas locales. Un valor más bajo indica mejores condiciones en las escuelas, con más maestros por cada estudiante.
- Proporción de población negra: Esta variable mide la proporción de la población de raza negra en la zona. Es calculada como 1000 * (proporción de población negra)^2.
- Porcentaje de población de bajo estatus socioeconómico: Representa el porcentaje de la población en la zona con un bajo nivel socioeconómico. Valores más altos indican áreas más desfavorecidas económicamente.
Con el código que has creado , busca la mejor red neuronal para que dado las características de un casa prediga el precio en miles de dólares de dicha casa
Los datos se obtienen de la siguiente forma:
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.model_selection import train_test_split from sklearn.datasets import fetch_openmldef get_datos(): boston=fetch_openml(name="boston",version=1) x=np.array(boston.data).astype(np.float32) y=np.array(boston.target).astype(np.float32) x_entrenamiento, x_validacion, y_entrenamiento, y_validacion = train_test_split(x, y, test_size=0.2, random_state=42) return x_entrenamiento, y_entrenamiento.reshape(-1,1), x_validacion, y_validacion.reshape(-1,1) |
Las redes a probar son:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
redes_neuronales=[ [[20,1],"relu"], [[20,1],"selu"], [[20,1],"tanh"], [[20,10,1],"relu"], [[20,10,1],"selu"], [[20,10,1],"tanh"], [[20,30,10,1],"relu"], [[20,30,10,1],"selu"], [[20,30,10,1],"tanh"], [[20,40,80,40,20,1],"relu"], [[20,40,80,40,20,1],"selu"], [[20,40,80,40,20,1],"tanh"], [[20,40,80,160,80,40,20,1],"relu"], [[20,40,80,160,80,40,20,1],"selu"], [[20,40,80,160,80,40,20,1],"tanh"] ] |
Nombre Capas Épocas Activación MSE R² Tiempo MSE R²
Red Entrenamiento Entrenamiento Entrenamiento Validación Validación
-------- -------------------------------- -------- ------------ --------------- --------------- --------------- ------------ ------------
1 [20, 1] 1000 relu 25.9839 0.700899 6.85148 26.1929 0.642826
2 [20, 1] 1000 selu 15.7143 0.819112 6.9331 19.6104 0.732587
3 [20, 1] 1000 tanh 52.4399 0.396364 7.04929 48.1765 0.343052
4 [20, 10, 1] 1000 relu 13.5203 0.844368 7.39035 18.5331 0.747278
5 [20, 10, 1] 1000 selu 15.3826 0.822931 7.63935 20.3983 0.721844
6 [20, 10, 1] 1000 tanh 27.3344 0.685353 7.49861 32.55 0.556139
7 [20, 30, 10, 1] 1000 relu 9.52126 0.890401 7.80591 14.8094 0.798054
8 [20, 30, 10, 1] 1000 selu 9.10227 0.895224 7.62227 14.83 0.797774
9 [20, 30, 10, 1] 1000 tanh 26.3255 0.696967 7.60604 29.6008 0.596355
10 [20, 40, 80, 40, 20, 1] 1000 relu 4.13976 0.952347 8.31231 22.1935 0.697363
11 [20, 40, 80, 40, 20, 1] 1000 selu 2.37718 0.972636 8.40947 17.5333 0.760911
12 [20, 40, 80, 40, 20, 1] 1000 tanh 17.7842 0.795286 8.34862 27.3635 0.626864
13 [20, 40, 80, 160, 80, 40, 20, 1] 1000 relu 3.40859 0.960764 9.40943 24.3886 0.66743
14 [20, 40, 80, 160, 80, 40, 20, 1] 1000 selu 2.96527 0.965867 9.57778 21.5213 0.706529
15 [20, 40, 80, 160, 80, 40, 20, 1] 1000 tanh 86.8838 -0.000119567 9.52437 74.7763 -0.0196708