Herramientas de usuario
Ocultar Menú
Traza:
−Barra lateral
clase:iabd:pia:2eval:tema07.metricas_regresion
¡Esta es una revisión vieja del documento!
7.c Metricas regresión
Hasta ahora hemos visto como definir una red neuronal y como entrenarla. El último paso que nos queda es saber si la red ha funcionado correctamente. Pero ¿Eso no se hacía con la función de coste? Pues no exactamente. La función de coste se usa para ayudar a ajustar los parámetros durante el entrenamiento mediante los datos de entrada pero no para saber si el modelo es bueno. Para saber si el modelo es bueno , se usan las métricas.
Las métricas son muy parecidas a las funciones de coste pero hay métricas que no existen como función de coste. El muchos casos la métrica será la misma que la función de coste.
En el método fit de Keras tenemos un nuevo parámetro para indicar la métrica llamado metrics que contiene un array con todas las métricas que queremos tener en nuestra red mientras se va entrenando
1 2 |
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=0.01),metrics=["AUC"])history=model.fit(x,y_true,epochs=20,verbose=False) |
Para obtener los valores de la métrica en cada época se usa la siguiente línea
1 2 |
history.history['auc']history.history['val_auc'] |
Validación
Acabamos de ver que entrenando la red neuronal , el error se consigue bajar a prácticamente cero. Es decir que los valores de los parámetros , pesos (weight) y sesgos bias, debe ser muy buenos. No exactamente. Resulta que los parámetros se han ajustado a los datos que le hemos pasado, pero ¿Como es de bueno el modelo para nuevos datos que no ha visto? Realmente ver como se comporta con datos nuevos y con los datos que ha ya visto es lo que nos va a decir como es de bueno nuestro modelo. Así que pasemos a ver como sacar las métricas también con datos nuevos.
Lo primero es averiguar de donde obtenemos nuevos datos. Normalmente no tenemos nuevos datos así que lo que hacemos es que solo vamos a entrenar nuestra red neuronal con el 80% de los datos y el 20% restante los guardaremos para validar la red neuronal. Eso lo vamos a hacer con la función train_test_split de scikit-learn
1 2 3 |
from sklearn.model_selection import train_test_splitx_train, x_test, y_train, y_test = train_test_split(x, y_true, test_size=0.2, random_state=42) |
La función train_test_split tiene los siguientes argumentos:
- Los primeros arrays son los datos a dividir entre los datos de entrenamiento o de validación (test en inglés).
test_size: La fracción de datos que se va a usar para la validación.Es un valor de 0.0 a 1.0. Siendo 0.0 que no hay datos para validación y 1.0 que todos sería para validación.Un valor aceptable detest_sizees entre0.2a0.3.random_state: Es para que sea reproducible el generador de los números aleatorios.- retorna los 4 array:
x_train: Array con laxde los datos de entrenamientox_test: Array con laxde los datos de validacióny_train: Array con layde los datos de entrenamientoy_test: Array con layde los datos de validación
Y ahora a Keras se los tenemos que pasar así:
1 |
history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=epochs,verbose=False) |
Lo datos de entrenamiento se pasan igual que antes pero los de validación se pasan en en un tupla en un parámetro llamado validation_data.
Por último tenemos que obtener la métrica para los datos de validación. Se obtiene igual que antes pero el nombre de la métrica empieza por val_
1 |
history.history['val_binary_accuracy'] |
Veamos un ejemplo completo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
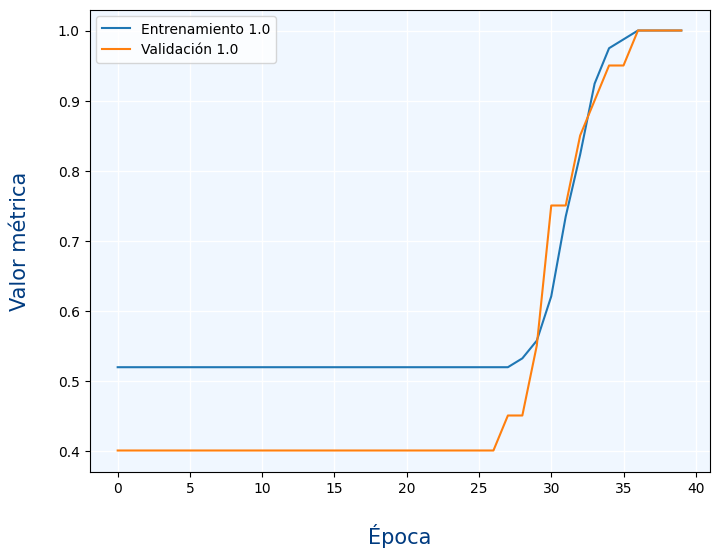
import numpy as npimport tensorflow as tfimport numpy as npimport pandas as pdimport kerasimport randomfrom keras.models import Sequentialfrom keras.layers import Densefrom sklearn.datasets import load_irisimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitiris=load_iris()x=iris.data[0:99,2]y_true=iris.target[0:99]np.random.seed(5)tf.random.set_seed(5)random.seed(5) x_train, x_test, y_train, y_test = train_test_split(x, y_true, test_size=0.2, random_state=42)model=Sequential()model.add(Dense(3, input_dim=1,activation="sigmoid",kernel_initializer="glorot_normal"))model.add(Dense(1,activation="sigmoid",kernel_initializer="glorot_normal"))model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adam(learning_rate=0.01),metrics=["binary_accuracy"])history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=40,verbose=False)figure=plt.figure(figsize=(8,6))axes = figure.add_subplot()axes.plot(history.history['binary_accuracy'],label="Entrenamiento "+str(history.history['binary_accuracy'][-1]))axes.plot(history.history['val_binary_accuracy'],label="Validación "+str(history.history['val_binary_accuracy'][-1]))axes.legend()axes.set_xlabel('Época', fontsize=15,labelpad=20,color="#003B80") axes.set_ylabel('Valor métrica', fontsize=15,labelpad=20,color="#003B80")axes.set_facecolor("#F0F7FF")axes.grid(b=True, which='major', axis='both',color="#FFFFFF",linewidth=1) |
Podemos ver en el gráfico que la métrica es muy similar con los datos de validación que con los de entrenamiento. otro detalle importante es que las métricas suelen ser buenas si su valor es 1 (al contrario de las funciones de pérdida en la que lo bueno era un 0)
Tipos de métricas de regresión
Son las métricas que se usan en problemas de regresión. Son casi las mismas que usábamos como funciones de coste.
- Mean Absolute Error (MAE)
- Mean Squared Error (MSE)
- Distancia del coseno
- Root Mean Squared Error (RMSE)
- Coeficiente de determinación o R²
Hay métricas que son exactamente iguales a las funciones de coste como MEA o MSE en los problemas de regresión MAE, MSE. Si ya las usamos como función de coste y queremos usarlas como métricas no es necesario indicarlas como métricas, se puede acceder a ellas de la siguiente forma:
Para mostrar la función de coste en el entrenamiento:
1 |
history.history['loss'] |
Para mostrar la función de coste en la validación:
1 |
history.history['val_loss'] |
Mean Absolute Error (MAE)
Es igual que la función de coste de Mean Absolute Error (MAE), así que no explicaremos nada mas sobre ella excepto como se usa en Keras como métrica
Se define como:
1 2 3 4 |
metrics=[tf.keras.metrics.MeanAbsoluteError()]metrics=["mean_absolute_error"]metrics=["mae"] |
y usarla como
1 2 3 4 5 |
history.history['mean_absolute_error']history.history['val_mean_absolute_error']history.history["mae"]history.history["val_mae"] |
Mas información:
Mean Squared Error (MSE)
Es igual que la función de coste de Mean Squared Error (MSE), así que no explicaremos nada mas sobre ella excepto como se usa en Keras como métrica
Se define como:
1 2 3 4 |
metrics=[tf.keras.metrics.MeanSquaredError()]metrics=["mean_squared_error"]metrics=["mse"] |
y usarla como
1 2 3 4 5 |
history.history['mean_squared_error']history.history['val_mean_squared_error']history.history["mse"]history.history["val_mse"] |
Mas información:
Distancia del coseno
Es igual que la función de coste de Distancia del coseno, así que no explicaremos nada mas sobre ella excepto como se usa en Keras como métrica
Se define en Keras como:
1 2 |
metrics=[tf.keras.metrics.CosineSimilarity()]metrics=["cosine_similarity"] |
y se usa como
1 2 |
history.history['cosine_similarity']history.history['val_cosine_similarity'] |
Mas información:
Root Mean Squared Error (RMSE)
La Root Mean Squared Error (RMSE) o Raiz cuadrada del error cuadrático medio se calcula igual que el MSE pero se le aplica la raíz cuadrada.
Por lo tanto su fórmula es
RMSE=√MSE=√1NN∑i=1(yi−^yi)2
Ahora vamos a explicar algunas cosas de RMSE.
- ¿Por qué se hace la raíz cuadrada? Pues porque antes habíamos elevado al cuadrado los errores
- ¿Pero que ventaja tiene esa raíz cuadrada? La raíz cuadrada se hace para que el error esté en las mismas unidades que los datos. Es para que como humanos entendamos mejor el valor. Es decir que nosotros entendemos mejor el resultado de RMSE que el de MSE
- ¿Por qué no existe la RMSE como función de coste? Por ahorrarnos el trabajo de hacer la raíz cuadrada. Como función de coste nos da igual el valor de MSE que la raíz cuadrada de MSE, la red va a funcionar igual.
- ¿Por qué no existe RMAE? Por que con MAE no elevábamos nada al cuadrado así que no tiene sentido RMAE
- A veces se intenta comprar los resultados de RMSE con MAE ya que ambos están en las mismas unidades.
- Por lo que si queremos usar MSE como métrica es mejor usar RMSE y como función de coste es mejor MSE
Se define en Keras como:
1 |
metrics=[tf.keras.metrics.RootMeanSquaredError()] |
y se usa como
1 2 |
history.history['root_mean_squared_error']history.history['val_root_mean_squared_error'] |
Mas información:
Coeficiente de determinación o R²
El coeficiente de determinación o R² se calcula de la siguiente forma:
R2=1−N∑i=1(yi−^yi)2N∑i=1(yi−ˉy)2 ˉy=1NN∑i=1yi−^yi
Siendo:
Ahora vamos a explicar algunas cosas de R²
- MAE, MSE y RMSE son mejor cuanto menor es el valor, mientras que R² es mejor cuanto más se acerca a 1.
- Un problema de R² es que aumenta su valor cuantas más variables tengamos de entrada (es decir el tamaño del vector de cada muestra) por eso se suele usar la métrica de R² ajustada. Para ello en Keras le pasaremos el argumento
num_regressorsa la claseRSquare
Se define en Keras como:
1 |
metrics=[tfa.metrics.RSquare()] |
y se usa como
1 |
history.history['r_square'] |
Mas información:
Selección de métricas de regresión
La elección de una métrica u otra se puede ver en MAE, MSE, RMSE, Coefficient of Determination, Adjusted R Squared — Which Metric is Better? y Know The Best Evaluation Metrics for Your Regression Model
- RMSE es mejor que MSE ya que está en las mismas unidades que el resultado y no al cuadrado.
- MAE vs MSE:
- MAE es mas robusto que MSE ante datos anómalos, es decir que los tiene menos en cuenta
- MSE eleva el error al cuadrado y la regresión al intentar minimizar dicho error , tiende a ir hacia ese dato anómalo. Por lo que MSE tiene más en cuenta los datos anómalos.
- Por lo tanto si los datos "anómalos" realmente no son anómalos sino situaciones "normales" pero poco frecuentes, deberíamos usar MSE, mientras que si los datos "anómalos" realmente son cosas "extrañas" que no deberíamos tener en cuenta, es mejor usar MAE.
clase/iabd/pia/2eval/tema07.metricas_regresion.1728633784.txt.gz · Última modificación: 2024/10/11 10:03 por admin
Herramientas de la página
Excepto donde se indique lo contrario, el contenido de este wiki esta bajo la siguiente licencia: GNU Free Documentation License 1.3