Herramientas de usuario
−Barra lateral
−Tabla de Contenidos
4. Gráficos
En este tema vamos a ver como crear gráficos en Python.
Para hacer gráficas hay varias librerías:
- Matplotlib: Es la librería mas antigua pero la mas utilizada.
- Seaborn: Es una capa por encima de Matplotlib y hace que sea mas sencillo hacer gráficas
- Yellowbrick: También es una capa encima de Matplotlib pero es una librería especializa en gráficas para Machine Learning
- Plotnine: Esta librería sigue una filosofía totalmente distinta a las anteriores. La forma de especificar una gráfica se basa en los descrito en el libro The Grammar of Graphics que es una forma mas moderna que la usada por Matplotlib. Esta forma de especificar una gráfica se usa principalmente en el lenguaje R con su librería ggplot2. Por lo que Plotnine imita a ggplot2
Mas información:
- Guía
- Colores:
Antes de empezar mira estas 2 gráficas (Shelly y Tuya) y dime si se parecen:
Obviamente no se parecen
Y ahora mira esta otra gráfica y dime si ahora se parecen (Shelly y Tuya):
En esta se parecen más.
Realmente la primera gráfica es el final de la segunda gráfica pero ambas gráficas están en una escala distinta.
El ejemplo está puesto para que se vea como se interpreta de una forma u otra una gráfica según la escala a la que esté. La primera gráfica está en la escala [ 650 W - 1050 W ] mientras que la segunda gráfica su escala es [0 W - 2500 W]
Por lo tanto, intenta que siempre las gráficas empiecen los ejes en 0.
Otro ejemplo lo tenemos en el siguiente video de Yotube: No te dejes engañar por un gráfico
Instalación e importación
Instalación
- Instalación con conda
1 |
conda install matplotlib |
Importación
- Importar matplotlib
1 |
import matplotlib.pyplot as plt |
Introducción
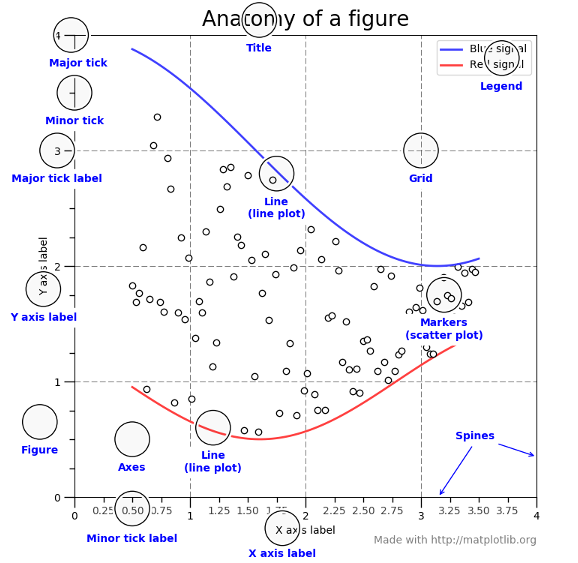
La base de los gráficos en Python es Matplotlib. Con esta librería hay una serie de conceptos que debemos conocer. Los nombres de los conceptos los vamos a decir en inglés para que se parezcan mas a los métodos, clases o argumentos de las librerías.
figure: Es como el "lugar" donde se van a colocar cada una de las gráficas. Siempre va a haber unafigure. Un problema configurees que en muchos ejemplos no se crea específicamente.axes: Es como cada una de las gráficas que vamos a crea dentro de unafigure.axis: Son cada uno de los ejes de una gráfica.
axes con axis.
- Crear la primera figura con su gráfica
1 2 3 4 |
import matplotlib.pyplot as pltfigure=plt.figure()axes = figure.add_subplot() |
Hemos creado una figura con figure=plt.figure(). Le hemos añadido un axes que es como la gráfica mediante axes = figure.add_subplot() y vemos que esa gráfica tiene por defecto unos axis o ejes en X e Y que van de 0 a 1.
add_subplot si realmente retorna un objeto Axes. Porque realmente el objeto que retorna es del tipo AxesSubplot. Lo podemos ver con el sigiente código:
1 |
print(type(axes)) |
<class 'matplotlib.axes._subplots.AxesSubplot'>
Organizar Axes
Veamos ahora como podemos organizar varias axes o gráficas en la misma figura.
El método add_subplot permite que le pasemos tres parámetros numéricos que indica el número de filas ,de columnas y la posición del gráfico.
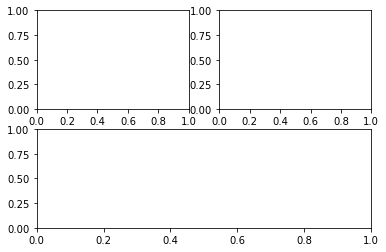
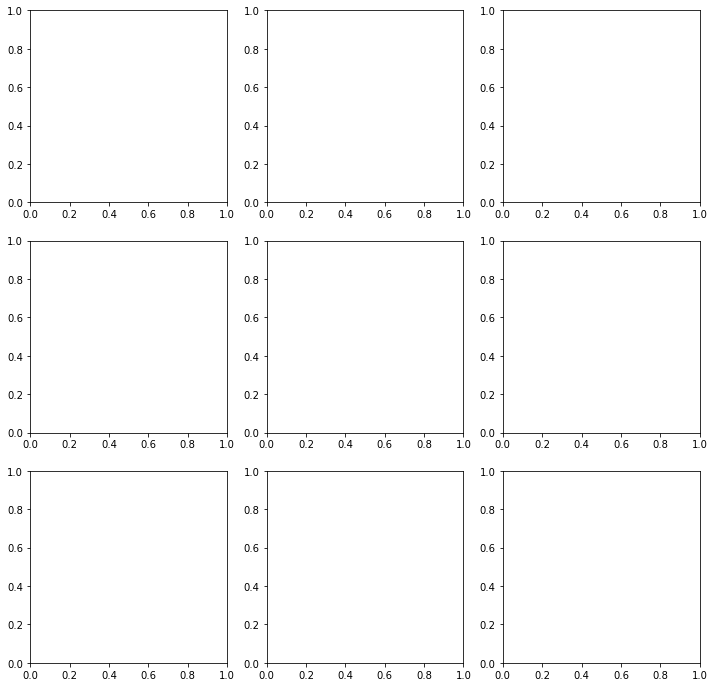
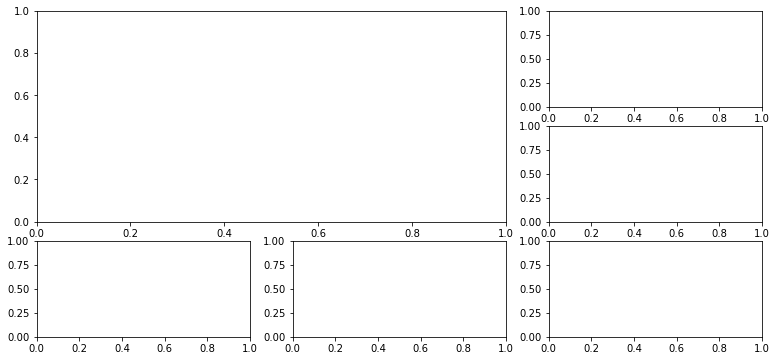
- Crea una rejilla de 2 filas , 2 columnas y añadir 3 gráficos en la posición ,en la posición 2 y en la posición 4 (la posición 3 se deja vacía)
1 2 3 4 5 6 |
import matplotlib.pyplot as pltfigure=plt.figure()axes = figure.add_subplot(2,2,1)axes = figure.add_subplot(2,2,2)axes = figure.add_subplot(2,2,4) |
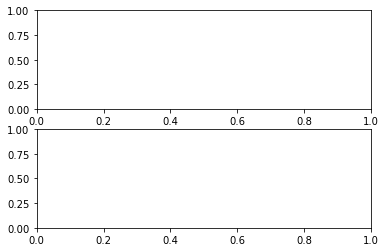
- Crea una rejilla de 2 filas , 1 columna y añadir 2 gráficos en la posición 1 y la posición 2.
1 2 3 4 5 |
import matplotlib.pyplot as pltfigure=plt.figure()axes1 = figure.add_subplot(2,1,1)axes2 = figure.add_subplot(2,1,2) |
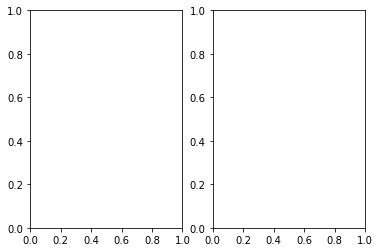
- Crea una rejilla de 1 fila , 2 columnas y añadir 2 gráficos en la posición 1 y la posición 2.
1 2 3 4 5 |
import matplotlib.pyplot as pltfigure=plt.figure()axes1 = figure.add_subplot(1,2,1)axes2 = figure.add_subplot(1,2,2) |
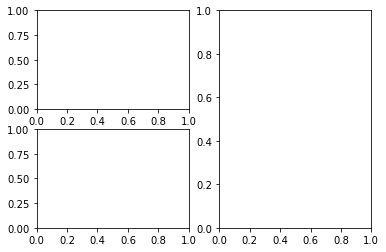
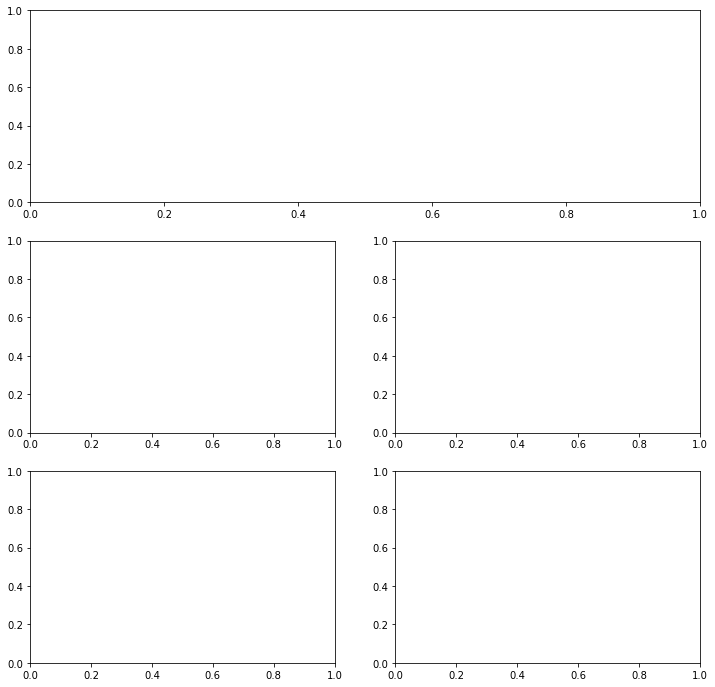
- Mezclar 2 organizaciones para figuras que no sean iguales.
1 2 3 4 5 6 |
import matplotlib.pyplot as pltfigure=plt.figure()axes = figure.add_subplot(2,2,1)axes = figure.add_subplot(2,2,3)axes = figure.add_subplot(1,2,2) |
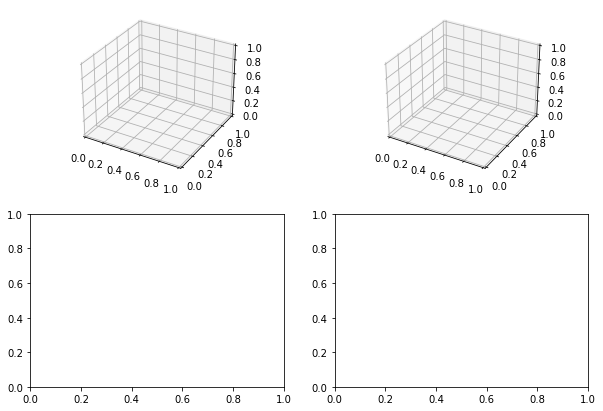
- Mezclar 2 organizaciones para figuras que no sean iguales.
1 2 3 4 5 6 |
import matplotlib.pyplot as pltfigure=plt.figure()axes1 = figure.add_subplot(2,2,1)axes2 = figure.add_subplot(2,2,2)axes3 = figure.add_subplot(2,1,2) |
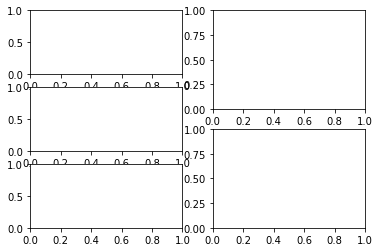
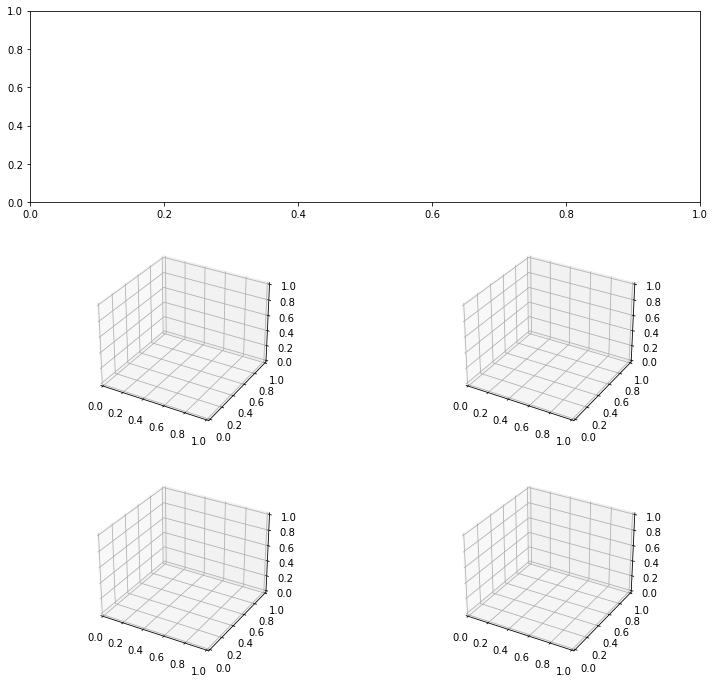
- Mezclar 2 organizaciones para figuras que no sean iguales.
1 2 3 4 5 6 7 8 |
import matplotlib.pyplot as pltfigure=plt.figure()axes1 = figure.add_subplot(3,2,1)axes2 = figure.add_subplot(3,2,3)axes3 = figure.add_subplot(3,2,5)axes4 = figure.add_subplot(2,2,2)axes5 = figure.add_subplot(2,2,4) |
Mas información:
Figura
Acabamos de ver como colocar cada gráfica dentro de la figura. Ahora veremos unas cosas mas sobre ella.
* Para hacer la figura mas grande solo hay que indicar el tamaño con el argumento figsize
1 |
figure=plt.figure(figsize=(15, 5)) |
El tamaño es el ancho y el alto en pulgadas.
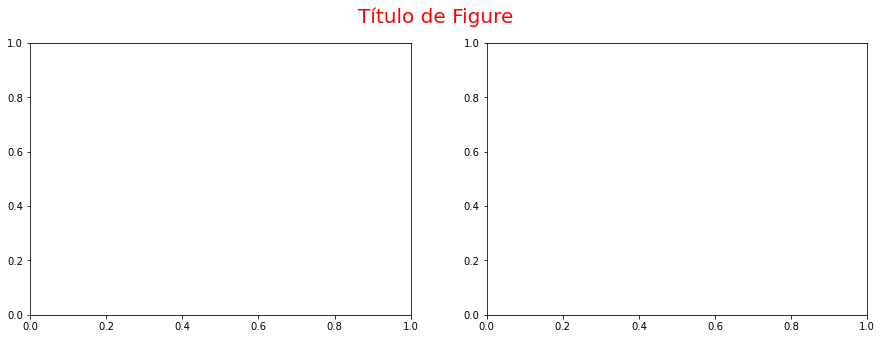
* Para indicar el título , el color y el tamaño de letra se usa el método suptitle
1 |
figure.suptitle("Título de Figure", fontsize=14, color='red') |
* Por último podemos grabar la figura entera con savefig
1 |
figure.savefig("nombre_fichero.png",facecolor="#FFFFFF",bbox_inches='tight') |
El argumento bbox_inches='tight' se usa para que no deje espacio alrededor de la imagen al guardarla.
Subfiguras
Además de figure y axes, a partir de matplolib 3.4 existe las subfigure. Éstas se pueden usar para poder poner un título común a varios axes.
Para ello se usa el método subfigures , indicando el número de filas y columnas. Este método retornará un array con todas las subfiguras. Cada subfigura será como una nueva figura.
1 |
subfigure_a,subfigure_b = figure.subfigures(nrows=2, ncols=1) |
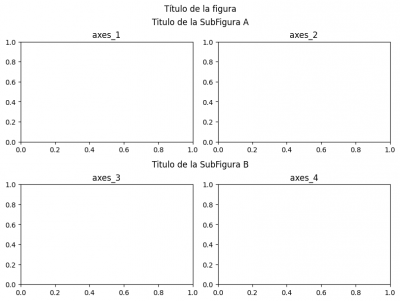
Veamos un ejemplo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import matplotlib.pyplot as pltfigure=plt.figure(figsize=(8, 6),layout='constrained')figure.suptitle("Título de la figura")subfigures = figure.subfigures(nrows=2, ncols=1).reshape(-1)subfigure_a=subfigures[0]subfigure_b=subfigures[1]subfigure_a.suptitle("Titulo de la SubFigura A")axes_1 = subfigure_a.add_subplot(1,2,1)axes_1.set_title("axes_1")axes_2 = subfigure_a.add_subplot(1,2,2)axes_2.set_title("axes_2")subfigure_b.suptitle("Titulo de la SubFigura B")axes_3 = subfigure_b.add_subplot(1,2,1)axes_3.set_title("axes_3")axes_4 = subfigure_b.add_subplot(1,2,2)axes_4.set_title("axes_4") |
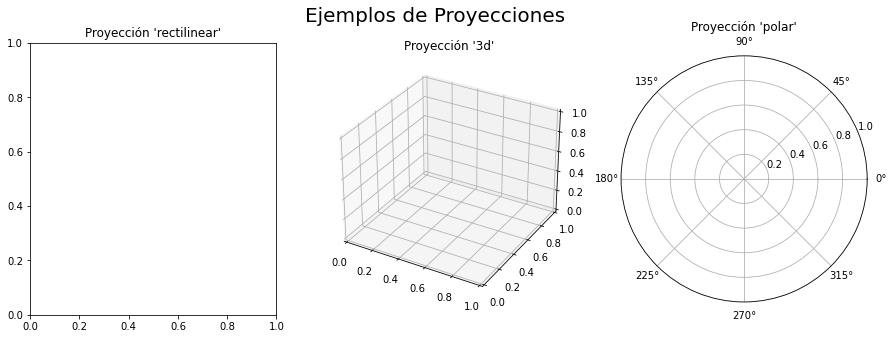
Proyecciones
Indicar como es la proyección de los ejes.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as pltfigure=plt.figure(figsize=(15, 5))figure.suptitle("Ejemplos de Proyecciones", fontsize=20)axes1 = figure.add_subplot(1,3,1,projection='rectilinear')axes1.set_title("Proyección 'rectilinear'")axes2 = figure.add_subplot(1,3,2,projection='3d')axes2.set_title("Proyección '3d'")axes3 = figure.add_subplot(1,3,3,projection='polar')axes3.set_title("Proyección 'polar'") |
Clase Figura
La siguiente clase permite simplificar la creación de Axes cuando queremos mostrar muchos en forma de matriz con varias columnas y muchas filas.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
class Figura: def __init__(self,ncols,naxes,axes_width_inches=6, axes_height_inches=None): self.ncols=ncols self.num_axes=naxes self.nrows=math.ceil(naxes/ncols) if axes_height_inches==None: axes_height_inches=axes_width_inches*0.86 self.figure, self.arr_axes = plt.subplots(ncols=self.ncols, nrows=self.nrows, figsize=(self.ncols*axes_width_inches,self.nrows*axes_height_inches), layout="constrained") if isinstance(self.arr_axes, (list, tuple, np.ndarray))==False: self.arr_axes=np.array([[self.arr_axes]]) def get_axes(self): return np.array(self.arr_axes).reshape(-1) |
El uso de la clase es la siguiente.
Imagina que quieres mostrar 12 Axes en 3 columnas y luego obtener cada uno de los axes.
1 2 3 4 |
figura=Figura(ncols=3,naxes=12)for axes in figura.get_axes(): axes.plot() |
La ventaja de esta clase es que no te tienes que preocupar del número de filas que va a haber. Que en este caso serán 4
Dibujando en 2D
Ahora veamos una serie de métodos para dibujar en un Axes o gráfica en 2 dimensiones
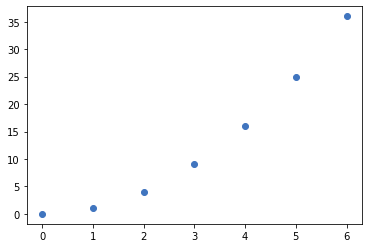
- Para dibujar una serie de puntos se usa el método
scatter
1 2 3 4 5 6 7 8 9 10 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()x=np.array([0,1,2,3,4,5,6])y=np.array([0,1,4,9,16,25,36])axes.scatter(x,y) |
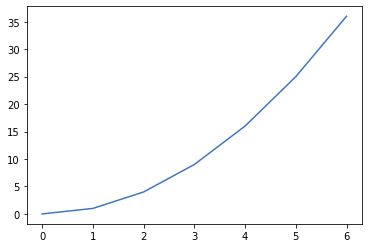
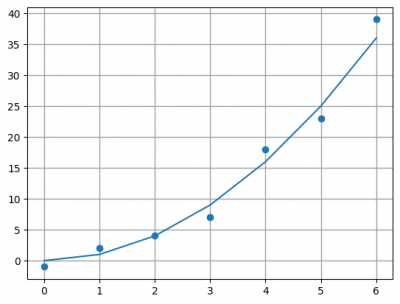
- Para dibujar una línea siguiendo una serie de puntos se usa el método
plot
1 2 3 4 5 6 7 8 9 10 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()x=np.array([0,1,2,3,4,5,6])y=np.array([0,1,4,9,16,25,36])axes.plot(x,y) |
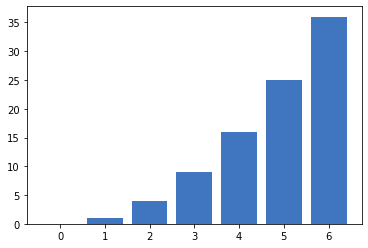
- Para dibujar una diagrama de barras en base a una serie de puntos se usa el método
bar
1 2 3 4 5 6 7 8 9 10 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()x=np.array([0,1,2,3,4,5,6])y=np.array([0,1,4,9,16,25,36])axes.bar(x,y) |
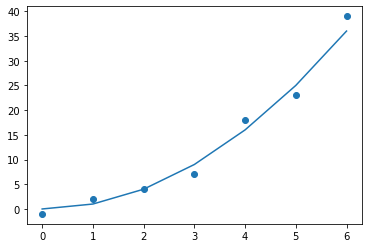
- En un mismo
Axesse pueden dibujar varias cosas a la vez
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()x1=np.array([0,1,2,3,4,5,6])y1=np.array([0,1,4,9,16,25,36])x2=np.array([0,1,2,3,4,5,6])y2=np.array([-1,2,4,7,18,23,39])axes.plot(x1,y1)axes.scatter(x2,y2) |
Dibujando en 3D
Ahora veamos una serie de métodos para dibujar en un Axes o gráfica en 3 dimensiones
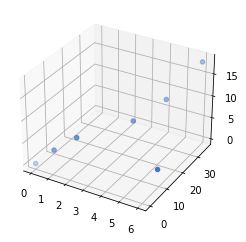
- Para dibujar una serie de puntos se usa el método
scatter, la diferencia es que se pasa lazy la proyección es3d.
1 2 3 4 5 6 7 8 9 10 11 12 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot(projection='3d')x=np.array([0,1,2,6,4,5,6])y=np.array([0,1,4,9,16,25,36])z=np.array([0,4,7,3,9,12,18])axes.scatter(x,y,z) |
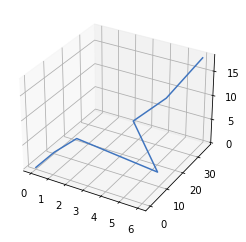
- Para dibujar una línea siguiendo una serie de puntos se usa el método
plot, la diferencia es que se pasa lazy la proyección es3d.
1 2 3 4 5 6 7 8 9 10 11 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot(projection='3d')x=np.array([0,1,2,6,4,5,6])y=np.array([0,1,4,9,16,25,36])z=np.array([0,4,7,3,9,12,18])axes.plot(x,y,z) |
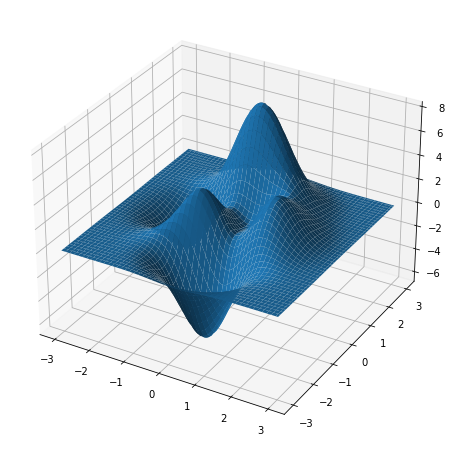
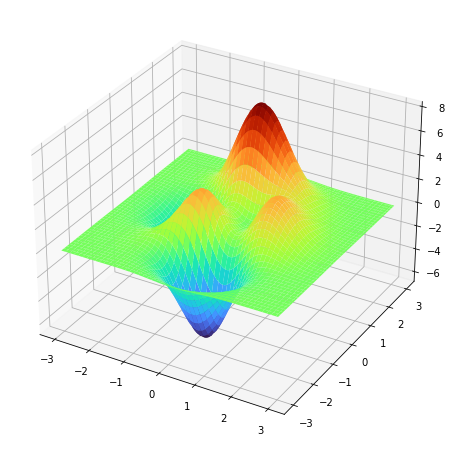
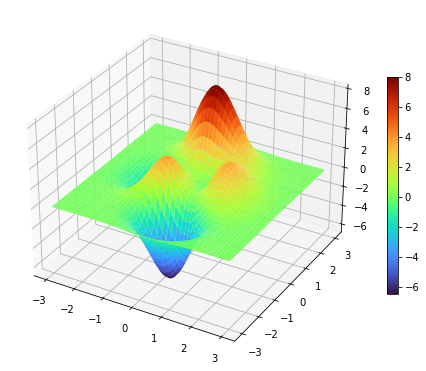
- Para dibujar una superficie en 3D se usa
plot_surface.
1 2 3 4 5 6 7 8 9 10 11 12 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize=(8,8))axes = figure.add_subplot(projection='3d')x=np.linspace(-3,3,100)y=np.linspace(-3,3,100)x,y=np.meshgrid(x,y)z = 3*(1 - x)**2 * np.exp(-x**2 - (y + 1)**2) - 10*(x/5 - x**3 - y**5)*np.exp(-x**2 - y**2) - 1./3*np.exp(-(x + 1)**2 - y**2) axes.plot_surface(x,y,z) |
z=3(1−x)2e−x2−(y+1)2−10(x5−x3−y5)e−x2−y2−13e−(x+1)2−y2
Añadir lo siguiente antes de los imports
1 |
%matplotlib widget |
o
1 |
%matplotlib ipympl |
y previamente haber instalado ipympl
conda install -c conda-forge ipympl
1 |
axes.view_init(45, -45) |
- Tambien podemos dibujar la superficie si solo tenemos unos pocos puntos y que interpole el resto. Para interpolar los puntos usamos
griddataen la funciónget_points_surface.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
import numpy as npimport matplotlib.pyplot as pltfrom scipy.interpolate import griddatadef get_points_surface(x,y,z): xi = np.linspace(min(x), max(x), 100) yi = np.linspace(min(y), max(y), 100) meshgrid_x, meshgrid_y = np.meshgrid(xi, yi) # Interpola los valores z en la malla meshgrid_z= griddata((x, y), z, (meshgrid_x, meshgrid_y), method='cubic') return meshgrid_x,meshgrid_y,meshgrid_z# Tenemos solo 50 puntosx = np.array([ 0.30478742, 1.24888694, -1.25457157, 0.06496563, 2.35768173, 2.37775853, -2.24648814, -1.75654273, -2.69119678, -0.35514094, -2.82074273, -0.25900065, 0.89486429, -1.3290763 , 1.05752941, 0.5451769 , -2.85610871, 0.35312453, -1.44448532, -0.50939282, -1.29884951, 1.15882751, -0.35727769, -2.05879357, 0.26789411, 1.68188859, -1.16181881, -1.6682527 , -0.67217245, 2.6183019 , 2.85597253, 1.03430206, 2.41700465, 2.07450523, -0.73203575, -2.44669795, 0.92046542, 0.34704457, -0.83061142, -1.64967297, -0.5608805 , -0.18635851, -1.38458653, -1.24924335, -0.2538816 , 2.16320348, 0.51751743, -1.29907283, -1.33213496, -0.27226755])y = np.array([-1.76753793, -1.79172773, 0.08421036, -2.47662379, -0.09848681, -0.82694273, 1.24611973, 1.48047734, 1.14655753, 1.13508248, -0.75839926, 1.00880883, -0.96090802, 0.43676322, -1.04515705, -0.3291297 , -2.63082642, -1.54394747, 2.82961564, -1.61649477, 1.14886507, 0.90286115, 1.34363484, -0.14946834, 0.57998265, -2.59818346, -2.56462717, -1.80614384, -2.08883402, -2.39937393, -2.22423681, 0.31966639, -1.87311105, 2.71260746, 1.08967067, 0.24611804, 1.2430836 , -1.41667997, 2.56035411, 2.03515835, 1.35791699, -0.11856026, 2.05261912, 1.46851394, 0.96195544, 2.4838516 , 0.80199338, -0.80435649, 0.31706744, -1.82171654])z = 3*(1 - x)**2 * np.exp(-x**2 - (y + 1)**2) - 10*(x/5 - x**3 - y**5)*np.exp(-x**2 - y**2) - 1./3*np.exp(-(x + 1)**2 - y**2) meshgrid_x,meshgrid_y,meshgrid_z=get_points_surface(x,y,z)figure = plt.figure(figsize=(10, 7))axes = figure.add_subplot(projection='3d')axes.plot_surface(meshgrid_x,meshgrid_y,meshgrid_z)# Añadimos los puntos originalesaxes.scatter(x, y, z, color='red') |
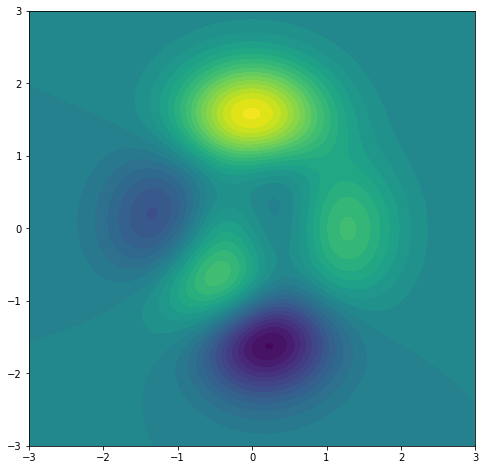
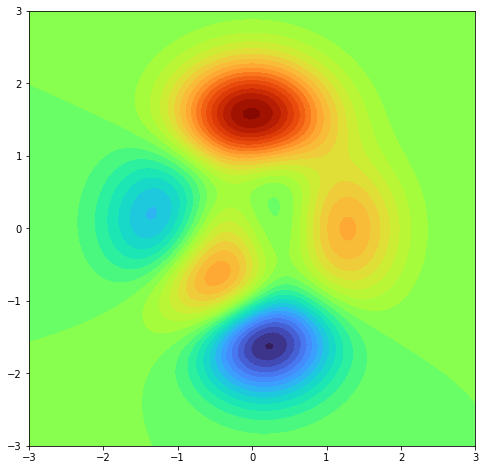
- Otra forma de dibujar superficies en 3D es mostrar el eje Z como colores similar a las curvas de nivel en los mapas topográficos, se usa el método
contourf. El parámetrolevelsindica el número de regiones distintas o curvas de nivel a mostrar.
1 2 3 4 5 6 7 8 9 10 11 12 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize=(8,8))axes = figure.add_subplot()x=np.linspace(-3,3,100)y=np.linspace(-3,3,100)x,y=np.meshgrid(x,y)z = 3*(1 - x)**2 * np.exp(-x**2 - (y + 1)**2) - 10*(x/5 - x**3 - y**5)*np.exp(-x**2 - y**2) - 1./3*np.exp(-(x + 1)**2 - y**2) axes.contourf(x,y,z,levels=30) |
Dibujando en 4D
Dibujar en 4D no es posible pero si lo que queremos es representar 2 variables en función de otras 2 variables , si que es posible mediante las siguientes técnicas:
- Variar el tamaño del punto en función de una variable
- Variar el color del punto en función de otra variable
Las 4 variables se mostrarían como:
- Eje X
- Eje Y
- Color
- Tamaño
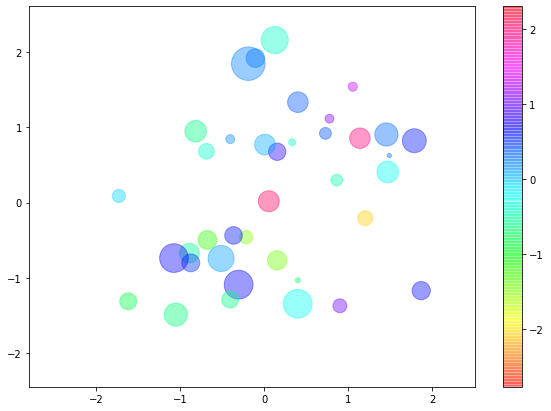
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize = (10, 7))axes = figure.add_subplot() random_state = np.random.RandomState(0)x = random_state.randn(100)y = random_state.randn(100)color = random_state.randn(100)size = 500 * random_state.randn(100) scatter=axes.scatter(x,y,c=color,s=size,cmap='hsv', alpha=0.4)figure.colorbar(scatter,ax=axes) |
Usamos el parámetro c que significa el color para mostrar el valor de z1, mientras que el parámetro s que significa el tamaño (size en inglés)) para mostrar el valor de z2. Es decir que en función de x e y, mostramos las 2 variables z1 y z2. Por último el parámetro de alpha es para hacer que los puntos sean un poco transparentes.
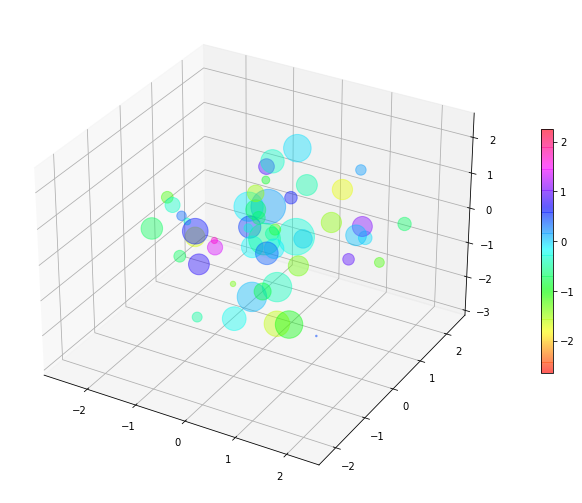
Dibujando en 5D
La técnica anterior se puede aplicar a una gráfica en 3D con lo que conseguimos representar hasta 5 variables distintas.
Las 5 variables se mostrarían como:
- Eje X
- Eje Y
- Eje Z
- Color
- Tamaño
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize = (16, 9))axes = figure.add_subplot(projection ="3d")random_state = np.random.RandomState(0)x = random_state.randn(100)y = random_state.randn(100)z = random_state.randn(100)color = random_state.randn(100)size = 500 * random_state.randn(100)scatter=axes.scatter(x,y,z,c=color,s=size,cmap='hsv', alpha=0.4)figure.colorbar(scatter,ax=axes, shrink = 0.5) |
Histogramas
Los histogramas consisten el mostrar la frecuencia con la que aparecen los valores en una secuencia unidimensional de datos. Podríamos pensar que son como diagramas de barras pero la información que muestran es de naturaleza distinta. En un diagrama de barras el origen de los datos es pares de números (x , y) , mientras que en un histograma solo existe la x.
Para hacer histogramas no vamos a usar la librería matplotlib sino una mas avanzada que está sobre ella llamada seaborn. Seaborn permite hacer cosas como matplotlib pero de una forma más sencilla.
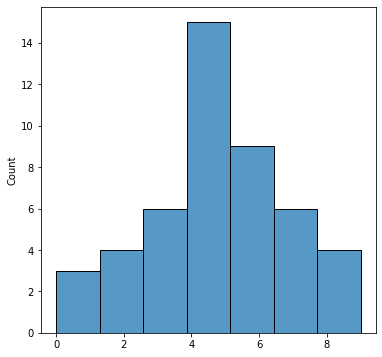
- Para dibujar un histograma se usa el método
histplotsobre el objetosns
1 2 3 4 5 6 7 8 9 10 |
import numpy as npimport matplotlib.pyplot as pltimport seaborn as sns figure=plt.figure(figsize = (6, 6))axes = figure.add_subplot()x=[0,1,4,3,4,5,6,7,6,5,4,3,2,1,2,3,2,3,4,5,6,5,6,7,8,7,6,5,4,4,5,6,7,8,9,8,7,6,5,6,7,6,5,4,3,2,3]sns.histplot(x=x,ax=axes) |
- Es necesaior importar la librería de seaborn con:
1 |
import seaborn as sns |
- El método
histplotpara dibujar el histograma ya no se aplica sobre el Axes sino sobresnspero hay que pasarle elaxesconax=axes
1 |
sns.histplot(x=x,ax=axes) |
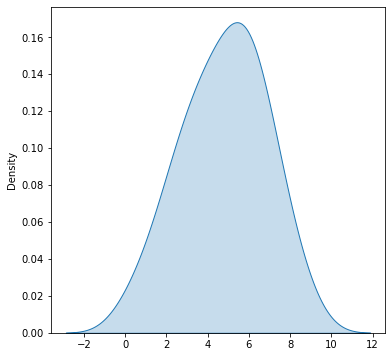
- Para dibujar el Kernel density estimation o KDE se usa el método
kdeplotsobre el objetosns
1 2 3 4 5 6 7 8 9 10 |
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfigure=plt.figure(figsize = (6, 6))axes = figure.add_subplot()x=[0,1,4,3,4,5,6,7,6,5,4,3,2,1,2,3,2,3,4,5,6,5,6,7,8,7,6,5,4,4,5,6,7,8,9,8,7,6,5,6,7,6,5,4,3,2,3]sns.kdeplot(x=x,fill=True,ax=axes) |
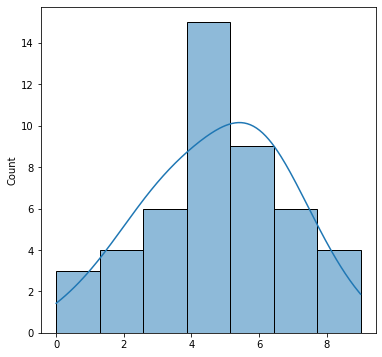
- Si queremos mostrar tanto el histograma como el KDE se usa el método
histplotpero sobre el objetosnspero con el parámetrokde=True
1 2 3 4 5 6 7 8 9 10 |
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfigure=plt.figure(figsize = (6, 6))axes = figure.add_subplot()x=[0,1,4,3,4,5,6,7,6,5,4,3,2,1,2,3,2,3,4,5,6,5,6,7,8,7,6,5,4,4,5,6,7,8,9,8,7,6,5,6,7,6,5,4,3,2,3]sns.histplot(x=x,kde=True,ax=axes) |
histplot y kdeplot no son iguales. Si dibujamos ambos en una mismo Axes e indicamos stat="density" en histplot vemos que son iguales. El motivo es que histplot puede mostrar los datos de distintas formas según el parámetro stat cuyas valores son count, frequency, probability o density. seaborn.histplot
1 2 |
sns.histplot(x=x,kde=True,ax=axes,label="histplot",stat="density", color="blue")sns.kdeplot(x=x,fill=True,ax=axes,label="kdeplot", color="green") |
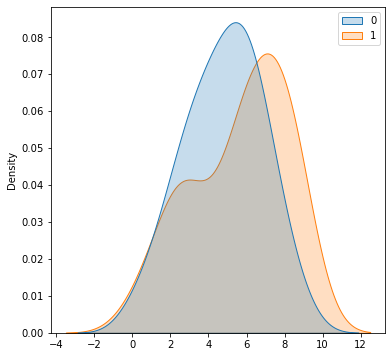
- Para dibujar el KDE pero para comparar 2 distribuciones, se usa el método
kdeplotsobre el objetosns
1 2 3 4 5 6 7 8 9 10 11 |
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfigure=plt.figure(figsize = (6, 6))axes = figure.add_subplot()x =[0,1,4,3,4,5,6,7,6,5,4,3,2,1,2,3,2,3,4,5,6,5,6,7,8,7,6,5,4,4,5,6,7,8,9,8,7,6,5,6,7,6,5,4,3,2,3, 1,2,3,7,8,5,3,7,8,9,9,6,8,0,9,8,6,3,2,7,6,5,3,6,7,4,8,9,7,2,1,6,5,3,2,3,5,6,7,8,7,8,7,5,6,9,8]tipo=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0, 1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]sns.kdeplot(x=x,hue=tipo,fill=True,ax=axes) |
Dibujando imágenes
Vamos ahora a tratar imágenes
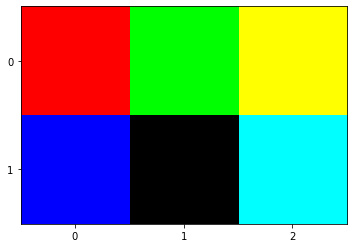
- Se pueden dibujar imágenes, simplemente indicando los colores de cada pixel como un tensor de colores.
1 2 3 4 5 6 7 8 9 10 11 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()imagen=np.array([[[255,0,0],[0,255,0],[255,255,0]],[[0,0,255],[0,0,0],[0,255,255]]])axes.xaxis.set_ticks([0,1,2])axes.yaxis.set_ticks([0,1])axes.imshow(imagen) |
Personalización
Veamos ahora una serie de métodos y parámetros para personalizar los Axes o gráficos.
Datos
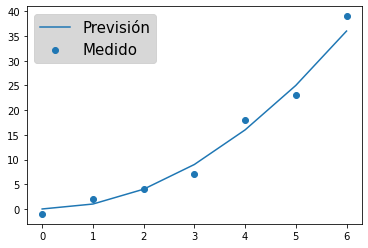
- Leyendas de los datos. En los métodos de
plotoscatterhay que indicar ellabely luego indicar que se muestre la leyenda conlegend
1 2 3 |
axes.plot(x1,y1,label="Previsión")axes.scatter(x2,y2,label="Medido")axes.legend(fontsize=15,facecolor='#CDCDCD',labelcolor="#000000") |
También es posible mostrar la leyenda poniendo los nombres directamente en el módulo legend en vez de en los métodos que dibujan como plot, scatter, etc.
1 2 3 |
axes.plot(x1,y1)axes.scatter(x2,y2)axes.legend(fontsize=15,facecolor='#CDCDCD',labelcolor="#000000",labels=["Previsión","Medido"]) |
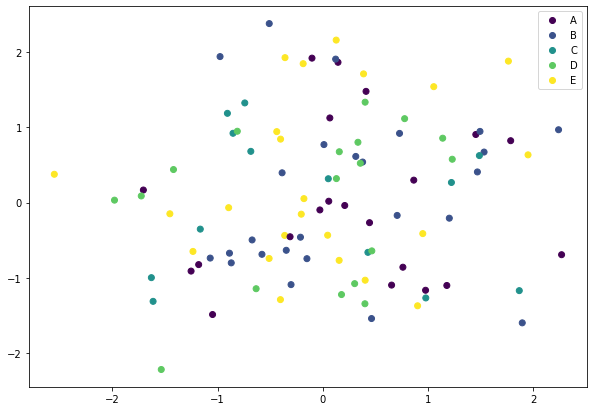
- Leyendas para colores: Podemos usar leyendas para cada tipo de color si mostramos los puntos con colores distintos. Para ello en el método
legendsusaremoshandles=scatter.legend_elements()[0]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure(figsize = (10, 7))axes = figure.add_subplot() random_state = np.random.RandomState(0)x = random_state.randn(100)y = random_state.randn(100)tipo = random_state.randint(5, size=100)labels_tipos=["A","B","C","D","E"] scatter=axes.scatter(x,y,c=tipo)legends=axes.legend(handles=scatter.legend_elements()[0],labels=labels_tipos) |
Si queremos saber el color que ha usado en cada tipo para poder reusar ese color para otra cosa, lo podemos hacer con:
1 2 |
index=0color=legends.get_lines()[index].get_color() |
Siendo index un valor entre 0 y len(labels_tipos)-1 ya que obviamente va a haber el mismo número de colores que elementos en el array de leyendas que es labels_tipos
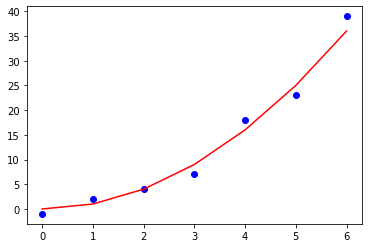
- Colores de los datos. Solo hay que indicar el argumento de
color.
1 2 |
axes.plot(x1,y1,color="#FF0000")axes.scatter(x2,y2,color="blue") |
También podemos obtener el siguiente color que vamos a usar con:
1 2 3 4 |
#Versiones nuevascolor=axes._get_lines.get_next_color()#Versiones antiguascolor=next(axes._get_lines.prop_cycler)['color'] |
color
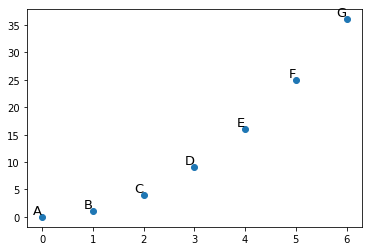
- Con el método
annotatepodemos anotar los datos.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import matplotlib.pyplot as pltimport numpy as np figure=plt.figure()axes = figure.add_subplot()x=np.array([0,1,2,3,4,5,6])y=np.array([0,1,4,9,16,25,36])labels=["A","B","C","D","E","F","G"]axes.scatter(x,y)for index,label in enumerate(labels): axes.annotate(label,xy=(x[index],y[index]),ha='right', va='bottom',fontsize=13) |
- Al usar
plotpodemos hacer que junto a la línea también salgan los puntos o incluso solo los puntos. Para ello se añade un tercer parámetro con el estilo del marker. Puedes ver todos los posibles estilos de markers en matplotlib.markers
1 |
axes.plot(x1,y1,"*-") |
Títulos
Establecer el título de cada eje Axis y del propio gráfico Axes.
1 2 3 |
axes.set_xlabel('Mes/Año', fontsize=15,labelpad=20,color="#003B80") axes.set_ylabel('Importe (€)', fontsize=15,labelpad=20,color="#003B80")axes.set_title("Gastos y Beneficios Mensuales", fontsize=20,pad=30,color="#003B80") |
Axes con el del figure.
Axes con título y label, se suelen solapar los textos entre ello. Para evitarlo, se debe añadir al final la orden:
1 |
figure.tight_layout() |
Color del Fondo
Ejes
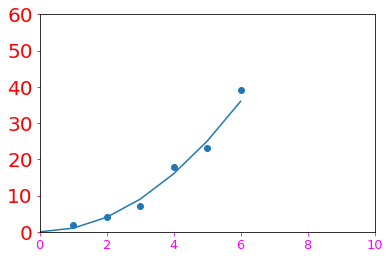
- Datos a mostrar en los ejes junto con el color , tamaño de fuente y el min/max
1 2 3 4 5 6 7 8 |
axes.xaxis.set_ticks([0,2,4,6,8,10])axes.yaxis.set_ticks([0,10,20,30,40,50,60])axes.tick_params(axis='x',labelsize=13, colors="#FF00FF")axes.tick_params(axis='y',labelsize=20, colors="#FF0000") axes.set_xlim(xmin=0,xmax=10)axes.set_ylim(ymin=0,ymax=60) |
- guías interiores (grid)
1 2 |
axes.grid(visible=True, which='major', axis='both',color="#A0A0A0",linewidth=1)axes.set_axisbelow(True) |
axes.set_axisbelow(True) para que el grid esté por debajo en el z-orden.
1 2 |
axes.minorticks_on()axes.grid(b=True, which='minor', axis='both',color="#A0A0A0",linewidth=1) |
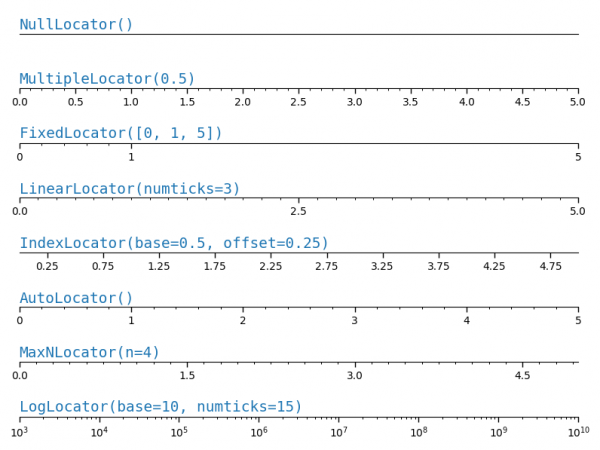
axes.xaxis.set_major_locator(locator)axes.yaxis.set_major_locator(locator)axes.xaxis.set_minor_locator(locator)axes.yaxis.set_minor_locator(locator)
Siendo los locator alguno de los siguientes:
NullLocatorMultipleLocatorFixedLocatorLinearLocatorIndexLocatorAutoLocatorMaxNLocatorLogLocator
- Que se importan como:
1 2 3 4 5 6 7 8 |
from matplotlib.ticker import NullLocatorfrom matplotlib.ticker import MultipleLocatorfrom matplotlib.ticker import FixedLocatorfrom matplotlib.ticker import LinearLocatorfrom matplotlib.ticker import IndexLocatorfrom matplotlib.ticker import AutoLocatorfrom matplotlib.ticker import MaxNLocatorfrom matplotlib.ticker import LogLocator |
Mas información:
- Hacer que los valores de los ejes siempre sean número enteros y no con decimales
1 2 3 |
from matplotlib.ticker import MaxNLocatoraxes.xaxis.set_major_locator(MaxNLocator(integer=True)) |
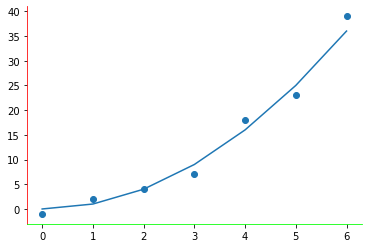
- Configurar las líneas de los ejes. Se pueden hacer invisibles o cambiar el color
1 2 3 4 |
axes.spines['right'].set_visible(False)axes.spines['top'].set_visible(False)axes.spines['left'].set_color("#FF0000")axes.spines['bottom'].set_color("#FF0000") |
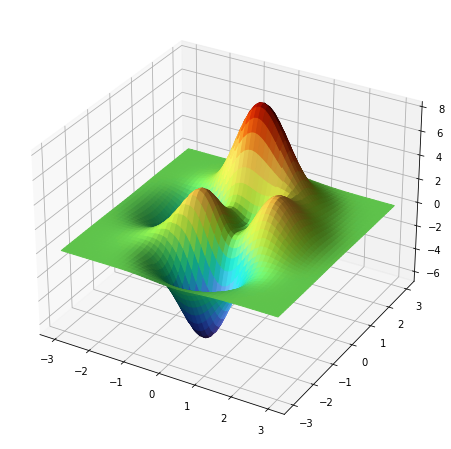
Superficies
- Al dibujar una superficie en 3D, podemos cambiar los colores en función del valor de
z. Para ello usamo el argumentocmap. Los posibles valores decmaplos podemos ver en Choosing Colormaps in Matplotlib
1 |
axes.plot_surface(x,y,z,cmap='turbo') |
1 |
axes.contourf(x,y,z,levels=30,cmap='turbo') |
cmap, además de como un string también se puede especificar como un objeto Python de la siguiente forma plt.cm.turbo
1 |
axes.plot_surface(x,y,z,cmap=plt.cm.turbo) |
- Podemos añadir una barra con los colores con el método
colorbar. Notar que el métodocolorbarse usa sobre la figura y hay que pasarle elAxes. Por último el parámetroshrinkes para que la barra no salga tan alta.
1 2 |
surface=axes.plot_surface(x,y,z,cmap='turbo')figure.colorbar(surface,ax=axes, shrink = 0.5) |
Otra forma de hacerlo es la siguiente:
1 |
figure.colorbar(plt.cm.ScalarMappable(cmap=plt.cm.turbo),ax=axes, shrink = 0.5) |
- Se pueden añadir sombreado a la imagen para que quede mas realista.
1 2 3 4 5 6 |
from matplotlib.colors import LightSourcelight_source = LightSource()facecolors = light_source.shade(z,plt.cm.turbo, blend_mode='soft')axes.plot_surface(x,y,z,facecolors=facecolors) |
Estableciendo el estilo
Es posible establecer el estilo general que usan los gráficos en mathplotlib. Es decir que tengan ya un aspecto predefinido.
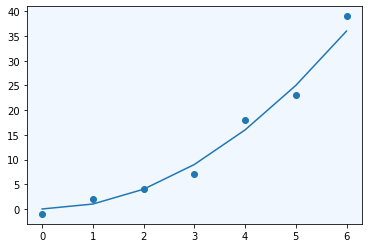
Simplemente con la línea plt.style.use('ggplot') tendrá el estilo que se usan en ggplot
Haciendo que los gráficos pasen de tener este estilo por defecto:
a tener este otro estilo:
Para saber los posibles estilos que hay , solo tenemos que ejecutar:
1 |
print(plt.style.available) |
1 2 3 4 5 6 7 8 9 |
[ 'Solarize_Light2', '_classic_test_patch', '_mpl-gallery', '_mpl-gallery-nogrid', 'bmh', 'classic', 'dark_background', 'fast', 'fivethirtyeight', 'ggplot', 'grayscale', 'seaborn-v0_8', 'seaborn-v0_8-bright', 'seaborn-v0_8-colorblind', 'seaborn-v0_8-dark', 'seaborn-v0_8-dark-palette', 'seaborn-v0_8-darkgrid', 'seaborn-v0_8-deep', 'seaborn-v0_8-muted', 'seaborn-v0_8-notebook', 'seaborn-v0_8-paper', 'seaborn-v0_8-pastel', 'seaborn-v0_8-poster', 'seaborn-v0_8-talk', 'seaborn-v0_8-ticks', 'seaborn-v0_8-white', 'seaborn-v0_8-whitegrid', 'tableau-colorblind10'] |
Como podemos ver hay muchos estilos relacionados con Seaborn
Definir el propio estilo
Normalmente queremos que todas nuestras gráficas tengan un mismo estilo , por ello es bueno crear una serie de funciones estándar que siempre usaremos.
- La primera función que usamos se llama
axes_configure_labels(axes,title,xlabel,ylabel)que configura tanto los labels como los colores y tamaños de fuente.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
def axes_configure_labels(axes,title,xlabel,ylabel): color="#003B80" facecolor="#FAFCFF" gridcolor="#BAD4F2" tickcolor="#011E32" fontsize_label=13 axes.set_xlabel(xlabel, fontsize=fontsize_label,color=color) axes.set_ylabel(ylabel, fontsize=fontsize_label,color=color) axes.set_title(title,color=color) axes.set_facecolor(facecolor) axes.spines['bottom'].set_color(tickcolor) axes.spines['top'].set_color(tickcolor) axes.spines['right'].set_color(tickcolor) axes.spines['left'].set_color(tickcolor) axes.tick_params(axis='both', colors=tickcolor) axes.grid(visible=True, which='major', axis='both',color=gridcolor,linewidth=1,zorder=-10) axes.set_axisbelow(True) handles, labels = axes.get_legend_handles_labels() if labels: axes.legend(fontsize=fontsize_label-2,labelcolor=color) |
- La siguiente función es
axes_configure_for_metrics(axes)que configura las gráficas para mostrar métricas que van de [0−1].
1 2 3 4 5 6 |
def axes_configure_axis_for_metrics(axes): axes.set_xlim(xmin=0,xmax=1) axes.set_ylim(ymin=0,ymax=1.1) axes.xaxis.set_major_locator(MultipleLocator(0.1)) axes.yaxis.set_major_locator(MultipleLocator(0.1)) |
- Para mostrar las gráficas de la pérdida en función de las épocas se usarán las funciones
axes_configure_axis_for_epochsyplot_history_metric:
1 2 3 4 |
def axes_configure_axis_for_epochs(axes,ymax=1): axes.xaxis.set_major_locator(MaxNLocator(10,integer=True)) axes.yaxis.set_major_locator(LinearLocator(10)) axes.set_ylim(ymin=0,ymax=ymax) |
1 2 3 4 5 6 7 8 9 |
def plot_history_metric(axes,history,metric_name,label=None,color="#003B80",decimales=2): if (label==None): label=metric_name axes.plot(history[metric_name],linestyle="dotted",c=color,label=f"{label}:{history[metric_name][-1]:.{decimales}f}") axes.plot(history['val_'+metric_name],linestyle="solid",c=color,label=f"Valid. {label}:{history['val_'+metric_name][-1]:.{decimales}f}") |
Usándose así:
1 2 3 4 5 6 |
figure=plt.figure(figsize=(6, 3.5))axes=figure.add_subplot(1,1,1)plot_history_metric(axes,history.history,"loss",decimales=6)axes_configure_labels(axes,"loss por épocas","Nº Épocas","Loss")axes_configure_axis_for_epochs(axes,1.1) |
Ejercicios
Ejercicio 1: Layout
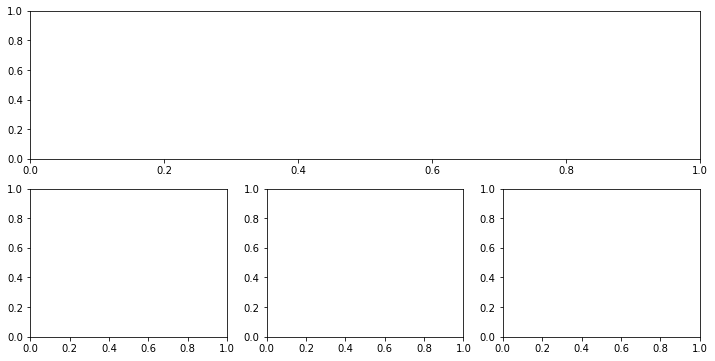
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 2: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 3: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 4: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 5: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 6: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 7: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 8: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 9: Layout
Crea una figura con los siguientes subplots:
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 10: tipos de gráficos 2D
Dado las variables x e y
1 2 |
x=[-3. , -2.57142857, -2.14285714, -1.71428571, -1.28571429, -0.85714286, -0.42857143, 0. , 0.42857143, 0.85714286, 1.28571429, 1.71428571, 2.14285714, 2.57142857, 3. ]y=[0.00443185, 0.01462444 , 0.04016108 , 0.09178317 , 0.17456307 , 0.27629519 , 0.36393672 , 0.39894228 , 0.36393672 , 0.27629519 , 0.17456307, 0.09178317 , 0.04016108 , 0.01462444 , 0.00443185] |
- Dibuja en una figura
xeycomo una serie de puntos. - Dibuja en una figura
xeycomo una linea continua. - Dibuja en una figura
xeycomo un diagrama de barras. - Dibuja en una figura
xeycomo una linea continua y además los puntos.
Además:
- Añade un título a la figura
- Guarda la figura a disco
Ejercicio 11: Layouts
Repite el ejercicio anterior pero ahora en una única figura como 4 subplots. Cada subplot deberá tener su título y la figura otro título
Ejercicio 12: numpy, linspace y gráficas
- Crea una variable llamada
xcon 300 números linealmente equidistantes entre el -2 y el 2. - Crea una variable llamada
yque sea el valor dexelevado al cuadrado. - Crea una figura en la que se muestre una línea de
xey
Además:
- Añade un título a la figura
- Guarda la figura a disco
- El nombre del eje "X" será "x"
- El nombre del eje "Y" será "x²"
Ejercicio 13: numpy, linspace y gráficas
- Crea una variable llamada
xcon 300 números linealmente equidistantes entre el -2 y el 2. - Crea una variable llamada
yque sea el valor absoluto dex - Crea una figura en la que se muestre una línea de
xey - El nombre del eje "X" será "x"
- El nombre del eje "Y" será "|x|"
Ejercicio 14: numpy, linspace y gráficas
- Crea una variable llamada
xcon 300 números linealmente equidistantes entre el -2 y el 2. - Crea una variable llamada
y1que sea el valor dexelevado al cuadrado. - Crea una variable llamada
y2que sea el valor absoluto dex - Crea una figura en la que se muestre:
- Una línea de
xey1de color verde - Una línea de
xey2de color rojo
- Establece un título en la figura
- Muestra una leyenda de forma que cada línea se llame "x²" y "|x|"
Ejercicio 15.A
Vamos a hacer un ejemplo sobre eficacia de la vacunación del COVID.
La siguiente función de python retorna 3 variables llamadas x , y y z.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
def get_data(): size=150 num_tipos=10 pendiente_base=-8 np.random.seed(6) x=np.array([]) y=np.array([]) z=np.array([]) x_ini=0 y_ini=50 z_ini=0 x_ancho=8 y_ancho=60 x_inc=2 y_inc=y_ancho-3 z_int=10 for i in range(0,num_tipos): pendiente=np.random.uniform(pendiente_base-0.4,pendiente_base+0.4,1)[0] x_tipo=np.random.uniform(x_ini,x_ini+x_ancho,size) y_tipo=np.random.uniform(y_ini,y_ini+y_ancho,size)+pendiente*x_tipo z_tipo=np.full(size, z_ini) x=np.concatenate((x,x_tipo)) y=np.concatenate((y,y_tipo)) z=np.concatenate((z,z_tipo)) x_ini=x_ini+x_inc y_ini=y_ini+y_inc z_ini=z_ini+z_int return x,y,z |
- La variable
xindica la cantidad de vacuna inyectada a los pacientes en ml - La variable
yindica la cantidad de pacientes que se han enfermado con COVID cada 100.000 habitantes. - La variable
zindica el rango de edad de los paciente.0=[0,10[ 10=[10,20[ 20=[20,30[, etc.
Ahora haz lo siguiente:
- Muestra un gráfico mostrando
- En el eje X la cantidad de vacuna inyectada
- En el eje Y la cantidad de pacientes que se han enfermado con COVID cada 100.000 habitantes.
- Muestra nombre de los ejes
Ejercicio 15.B
Muestra ahora el mismo gráfico pero añadiendo:
- Haz una regresión lineal con los datos y añade esa recta a la gráfica. El color de la recta debe ser negra.
Para hacer la regresión usa la siguiente función:
1 2 3 4 5 6 7 8 9 10 11 |
from sklearn.linear_model import LinearRegressiondef get_recta_regresion(x,y): model = LinearRegression() model.fit(x.reshape(-1, 1), y.reshape(-1, 1)) x_init=x.min() y_init=model.predict([[x_init]])[0,0] x_fin=x.max() y_fin=model.predict([[x_fin]])[0,0] return [x_init,x_fin],[y_init,y_fin] |
Esta función retorna los puntos iniciales y finales de la recta de la regresión pero lo primero que retorna son las x's de los 2 puntos y luego las y's de los 2 puntos.
Se ha hecho así para que sea fácil de dibujar la recta con la función plot
Explica la relación entre mayor dosis de vacuna y la cantidad de pacientes que se han infectado con COVID.
Ejercicio 15.C
Muestra ahora el mismo gráfico pero añadiendo:
- Que se muestre cada punto de un color distinto según el rango de edad (La variable
z). - Muestra una leyenda para cada uno de los "colores". Sabiendo que cada color realmente corresponde a un rango de edad.
- Quita el ajuste lineal que habías hecho.
Ejercicio 15.D
Muestra ahora el mismo gráfico pero añadiendo:
- Añade ahora una regresión lineal pero ahora haz una regresión distinta para cada rango de edad.
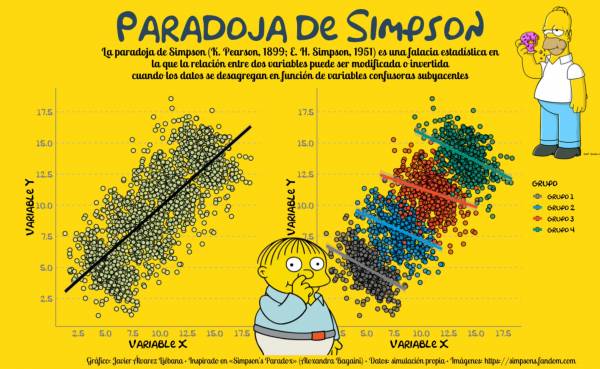
Vuelve a explicar la relación entre mayor dosis de vacuna y la cantidad de pacientes que se han infectado con COVID pero teniendo en cuenta la edad.
Lo que acabas de observar se llama la paradoja de Simpson. La paradoja de Simpson
Ejercicio 15.E
Vuelve a explicar los datos anteriores si:
xes el número de policías negros en EEUUyes el número de delitos
Ahora vuelve a explicar los datos si:
zes el PIB de cada estado de EEUU
Ejercicio 16: plot_surface
Dibuja una superficie en 3D , sabiendo que:
x∈[−15,15]
y∈[−15,15]
z=sin(√x2+y2+4)√x2+y2+4
Haz que se muestre:
- En cada eje su nombre X, Y , Z.
- Con Sombreado
- Cambiando el color map para que sea el llamado
cool - Muestra el colorbar
Ejercicio 17:contourf
Dibuja una superficie en 3D pero como curvas de nivel de distintos colores (debes usar contourf), sabiendo que:
x∈[−15,15]
y∈[−15,15]
z=sin(√x2+y2+4)√x2+y2+4
Además:
- En cada eje su nombre X, Y.
- Cambia el color map por el llamado
cool - Muestra el colorbar
Ejercicio 18: sns.kdeplot
Muestra el Kernel density estimation (KDE) ( es como el histograma pero como una línea continua) de diversas alturas de hombre y de mujeres
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
altura_hombres=[182.74607218, 169.32946152, 169.83096949, 166.56218827, 178.19244578, 159.19076782, 183.46887059, 168.43275859, 174.91423458, 171.50377775, 181.77264762, 160.63915574, 171.06549678, 170.69567387, 179.80261665, 166.4006524 , 171.96543075, 167.73284949, 173.25328248, 176.49689128, 166.39628494, 179.86834226, 178.40954432, 176.01496603, 178.4051357 , 168.89763284, 172.26265865, 167.38538339, 171.39267152, 176.1821328 , 168.85003549, 170.61947884, 168.8769638 , 167.92876615, 168.97252321, 172.92401241, 166.29613791, 174.40649419, 182.95881306, 177.45226496, 171.84898669, 167.67422622, 168.51705024, 183.15472761, 173.30484653, 169.17802612, 174.14549291, 185.60153082, 173.72095371, 176.70321866, 174.80102192, 170.88650092, 166.14489081, 170.90394367, 171.7466346 , 176.51973915, 178.03390048, 178.58661249, 174.71352395, 178.31084699, 168.47361235, 180.51720893, 176.07757892, 171.21144299, 175.93110888, 172.54656972, 179.78977632, 182.1189009 , 186.11345244, 164.62102199, 164.33531717, 169.97320482, 173.96022242, 178.25701353, 174.89380968, 160.86679271, 171.16277592, 177.96784786, 174.38056841, 177.57206708, 171.66603114, 171.79545159, 174.11936835, 175.46030988, 174.18979832, 173.71405187, 168.97602628, 175.26538272, 173.73092763, 179.77690345, 180.19350728, 174.1109385 , 170.7482903 , 169.16761756, 175.54096612, 173.46404041, 170.93687795, 173.26158114, 169.27999494, 177.1881922 ]altura_mujeres=[159.31722861, 169.34704623, 164.42094985, 165.56147114, 155.43052893, 163.0162946 , 166.44333871, 156.27779639, 160.40268896, 162.19568728, 153.76129608, 163.89095635, 167.07696389, 156.84290436, 164.10327587, 154.12629953, 161.76782694, 152.30536587, 168.72850625, 164.45340323, 161.85229826, 157.34903028, 169.64253558, 173.8026105 , 150.85210881, 169.41698418, 171.76590452, 164.02807018, 154.80439181, 167.18007191, 160.91447819, 158.37647623, 154.61965119, 165.30322498, 166.7568412 , 158.25881562, 165.12345802, 155.13395166, 166.81116619, 162.27940379, 160.88058137, 161.38952476, 167.21331694, 166.50246984, 165.17679195, 162.82620726, 162.46692677, 165.71028157, 163.39496736, 166.09530844, 160.13929936, 147.39097342, 168.23294761, 175.12187788, 164.64818666, 161.3990686 , 161.18133154, 161.28567487, 162.10445645, 155.26788763, 158.89743325, 156.01783903, 163.49279497, 160.22015309, 164.97126794, 160.95178104, 167.91801113, 163.28120341, 175.14419837, 150.62183446, 158.11849987, 167.40892135, 177.16995424, 160.50819133, 162.26201396, 160.64211454, 169.98874268, 160.27615282, 166.08041904, 160.08119041, 154.36464747, 163.88128632, 165.01910888, 169.7593553 , 161.33731784, 158.29582762, 165.37656658, 163.44442255, 163.68399046, 161.56132378, 168.96203142, 164.2169563 , 173.42795225, 168.66634019, 165.95429878, 152.23536996, 165.61391568, 164.52169322, 166.86571004, 168.26665257] |
Muestra los datos:
- En el mismo subplot
- Que las etiquetas sean "Hombre" y "Mujer"
- Titulo de la figura
- La etiqueta del eje X sea "Edad"
- La etiqueta del eje Y sea "Densidad"
Ejercicio 19: sns.histplot
Repite el ejercicio anterior pero ahora muestra los datos como un histograma y haz que tengan colores distintos.
Ejercicio 20
Busca las cosas raras que hay en el siguiente código y explica como las harías tu.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import pandas as pddf = pd.read_csv("fifa.csv")plt.figure(figsize=(10, 6))ax = sns.scatterplot(x ='work_rate', y = df['wage_eur'], hue = "league_rank", data = df, palette = ["green", "red", "coral", "blue"], legend="full", alpha = 0.4 )max_wage_eur = df.groupby("work_rate")["wage_eur"].max()#Making a line plot of max wagessns.lineplot(data = max_wage_eur, ax = ax.axes, color="grey")ax.tick_params(axis= "x", rotation=90)plt.xlabel("Work Rate")plt.ylabel("Wage EUR")plt.title("Relationship between work rate and wage by league rank", fontsize = 18)plt.show() |
El código está sacado de la página: Exploratory Data Analysis with Some Cool Visualizations in Python’s Matplotlib and Seaborn Library
Ejercicio 21: imshow
El fichero mario.csv que hay dentro de mario.zip contiene un array de numpy.
Carga ese array y sabiendo que contiene una imagen de tamaño 41x31 y que cada color son 3 números, haz con matplotlib que se muestre la imagen de Mario Bros.
Fíjate que en la imagen no debe salir ninguno de los ejes.
Ejercicio 22.A
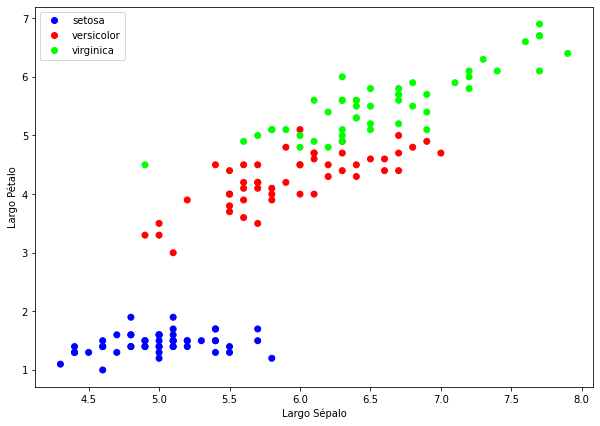
Para la red de las flores, muestra para todos los tipos de flores una gráfica de puntos de forma que:
- El eje X será el largo del sépalo y pon eso como etiqueta del eje
- El eje Y será el largo del pétalo y pon eso como etiqueta del eje
- Que cada tipo de flor sea de un color distinto.
Ejercicio 22.B
Repita el ejercicio anterior pero ahora la creación del gráfico se hará en la función llamada plot_single_scatter con los argumentos:
axes:Axes donde se dibujaráx:Array con los valores de la Xy:Array con los valores de la Ytarget:Array con el Tipo de florlabel_x:Label del eje Xlabel_y:Label del eje Y
Esa función deberá hacer la misma gráfica del ejercicio anterior.
Ejercicio 22.C
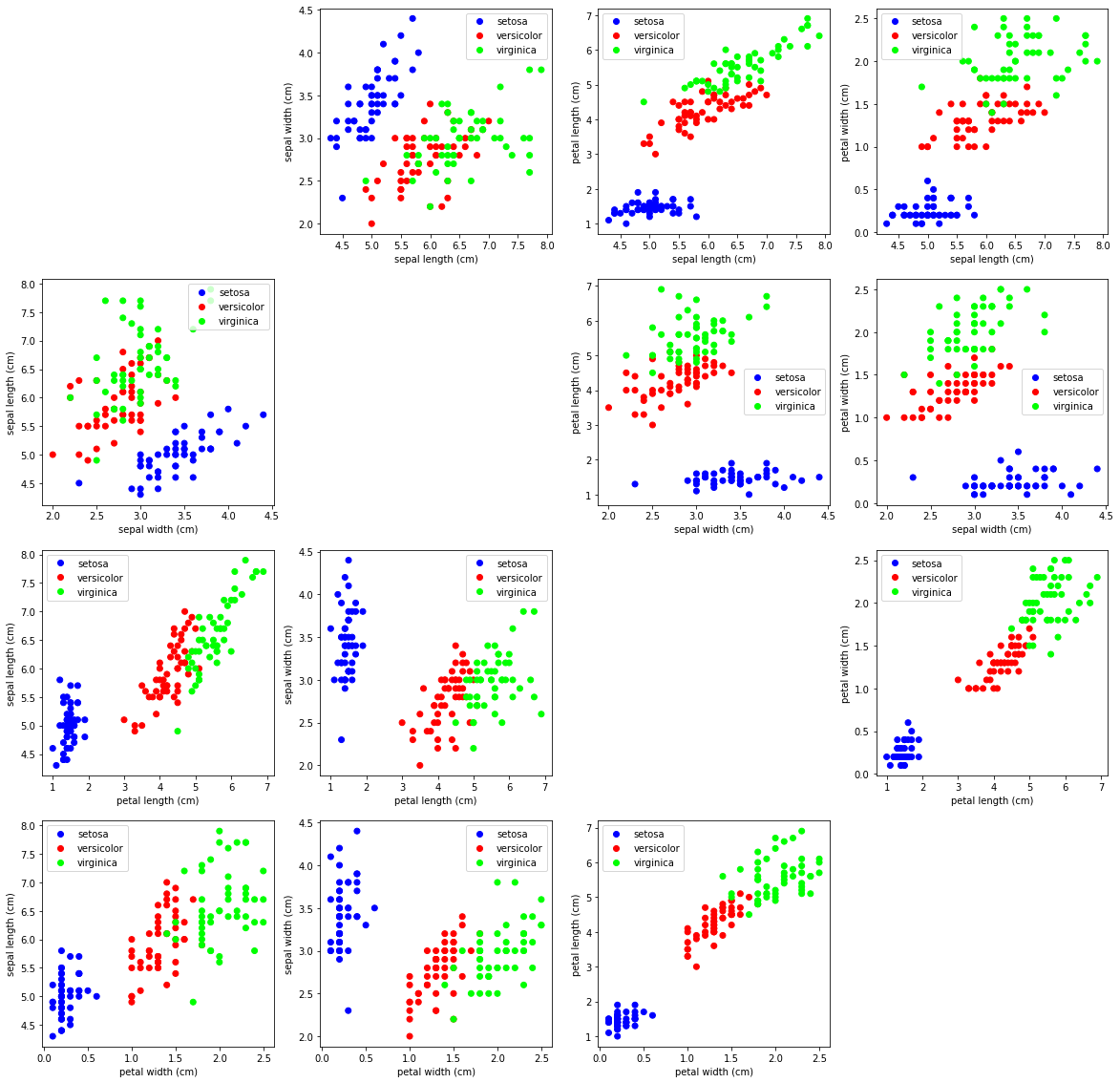
Usando la función plot_single_scatter, muestra varias gráficas de forma que se muestren todas las características vs todas las otras características. Pero no deberás mostrarlo si son iguales las características.
La gráfica debe quedar como la siguiente:
Ejercicio 22.D
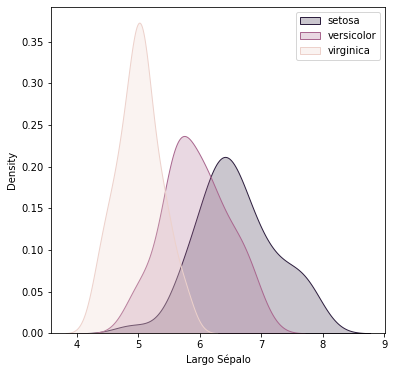
Muestra un gráfico KDE con la distribución de cada tipo de flor en función del largo del sépalo
- La etiqueta del eje X sea "largo sépalo"
Ejercicio 22.E
Repita el ejercicio anterior pero ahora la creación del gráfico se hará en la función llamada plot_single_kde con los argumentos:
axes:Axes donde se dibujaráx:Array con los valores de la Xtarget:Array con el Tipo de florlabel_x:Label del eje X
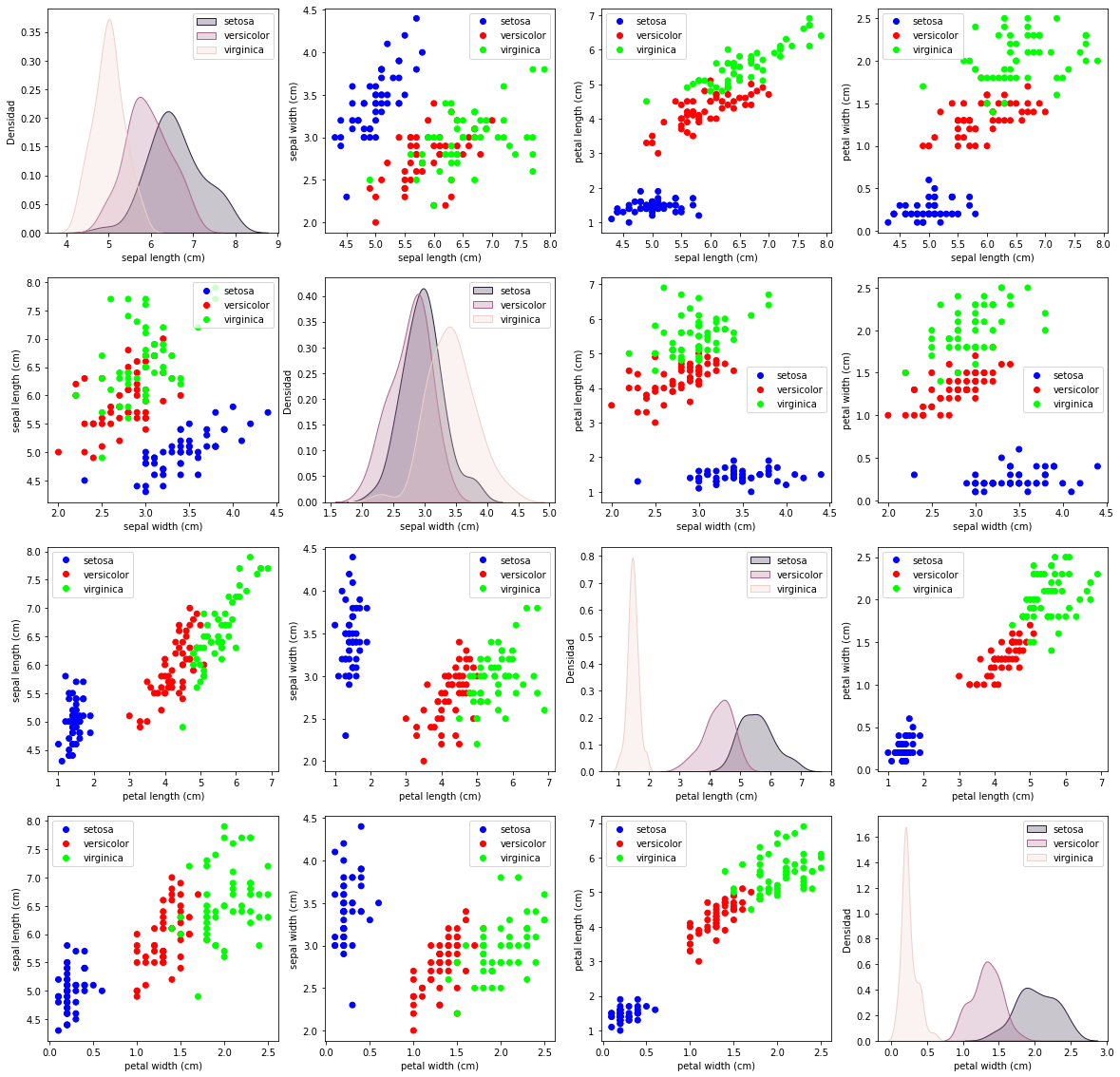
Ejercicio 22.F
Usando la función plot_single_kde, modifica el gráfico anterior de forma que donde había los huecos, se llame a la función plot_single_kde
La gráfica debe quedar como la siguiente:
Ejercicio 22.G
Ejecuta el siguiente código en Python:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import numpy as npimport pandas as pdimport seaborn as snsfrom sklearn.datasets import load_irisiris=load_iris()#Obtener los datosdata=iris.datatarget=iris.targetfeature_names=['longitud sepalo ','ancho sepalo','longitud petalo','ancho petalo'] #iris.feature_namestarget_names=['setosa', 'versicolor', 'virginica'] #iris.target_namestarget_unique=[0,1,2] #np.unique(target)#Crear el DataFrame con los datosdf=pd.DataFrame(data, columns=feature_names)df['flores']=targetdf['flores'] = df['flores'].replace(target_unique,target_names)#Crear el gráficosns.pairplot(df,hue="flores") |
¿Que sorpresa te has llevado?
Ejercicio 23.A
De la primera red neuronal de las flores que hemos usado en el tema 1, muestra una gráfica en la que se muestre:
- Eje X: Nº de época
- Eje Y: Valor de la función de pérdida. Recuerda que los datos están en
history.history['loss'] - Personaliza el gráfico de la forma siguiente:
- El tamaño de la figura será de (7 y 5)
- Eje X:
- El label será "Nº Épocas", con color "#003B80" y tamaño de fuente 13
- Los números que parecerán serán siempre números enteros y no con decimales
- Eje Y:
- El label será "Métricas" con color "#003B80" y tamaño de fuente 13
- Se verá del 0 al 1.1
- Los números a salir los números del eje Y serán 0.1, 0.2, etc
- El título del subplot será "Red:" y el número de neuronas de cada capa.
- El color del fondo es
#F0F7FF - Que se vea el grid de los ejes de color blanco con ancho de las líneas de 2 píxeles.
- Para que la línea salga punteada para ello usa
linestyle="dotted"en el métodoplot - El número que se muestra en la leyenda es "loss entrenamiento:" y el valor en loss la última época con 2 decimales
Para el entrenamiento se usarán 40 épocas
Ejercicio 23.B
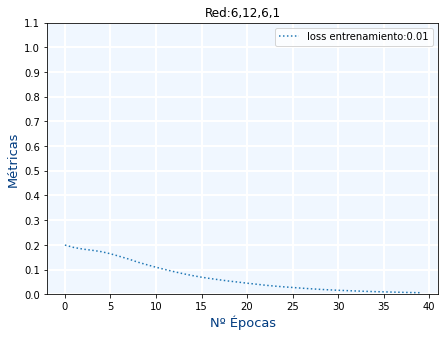
Crea una función de Python llamada plot_metrics(axes,history,title) de forma que salga el mismo gráfico que en el ejercicio anterior
A la función la debes llamar de usa forma similar a la siguiente:
1 2 3 4 5 6 |
history=model.fit(x, y,epochs=40,verbose=False)figure=plt.figure(figsize=(7, 5))axes = figure.add_subplot(1,1,1)plot_metrics(axes,history.history,"Red:6,12,6,1") |
Ejercicio 23.C
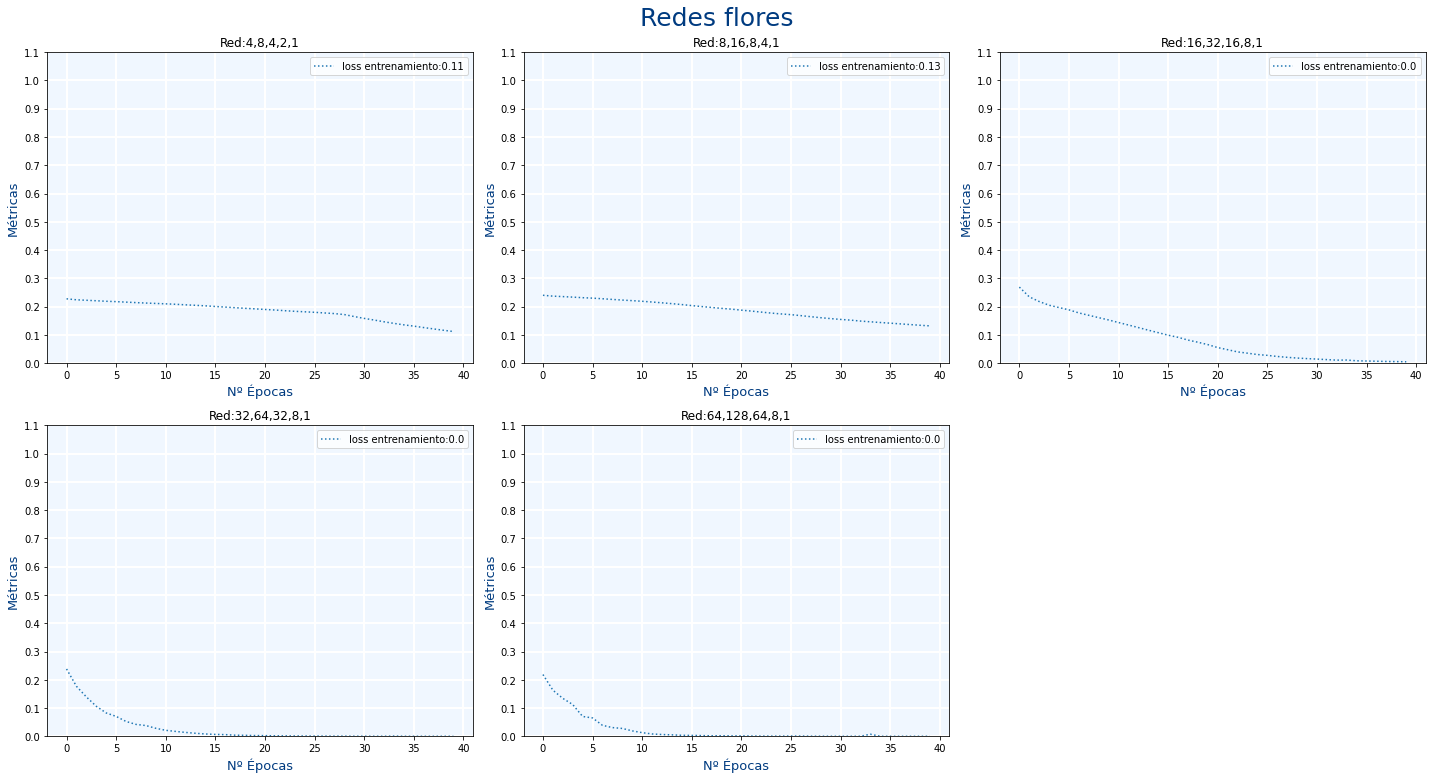
Usando la función plot_metrics muestra las gráficas de las pérdidas por épocas de las siguientes redes neuronales:
| Nº Neuronas en cada capa |
|---|
| 4, 8, 4, 2, 1 |
| 8, 16, 8, 4, 1 |
| 16, 32, 16, 8, 1 |
| 32, 64, 32, 8, 1 |
| 64, 128, 64, 8, 1 |
Además:
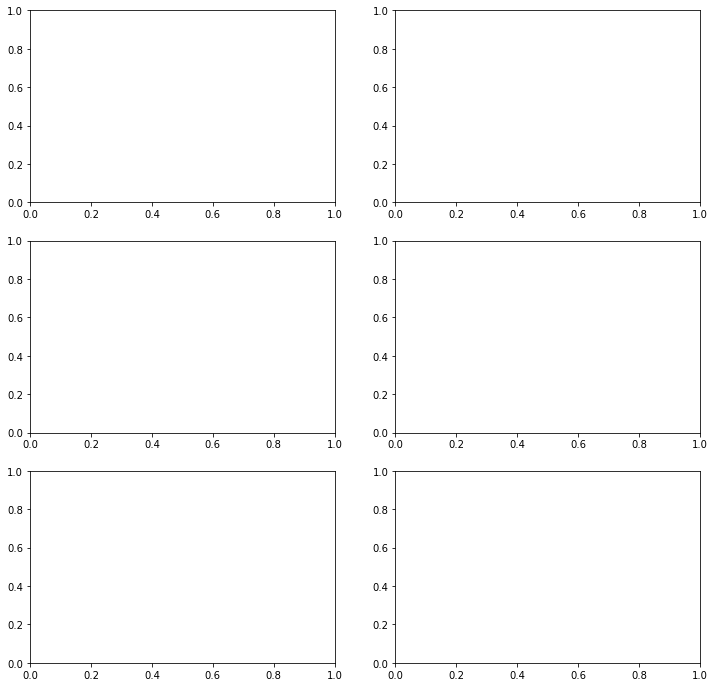
- Deberás mostrar los 5 subplots en la disposición de 2 filas y 3 columnas
- El título de la figura será "Redes flores"
- El Nº de épocas será 40.
Indica para cada red, a partir de que época ya no habría sido necesario seguir entrenando dicha red y cuales son las mejores redes
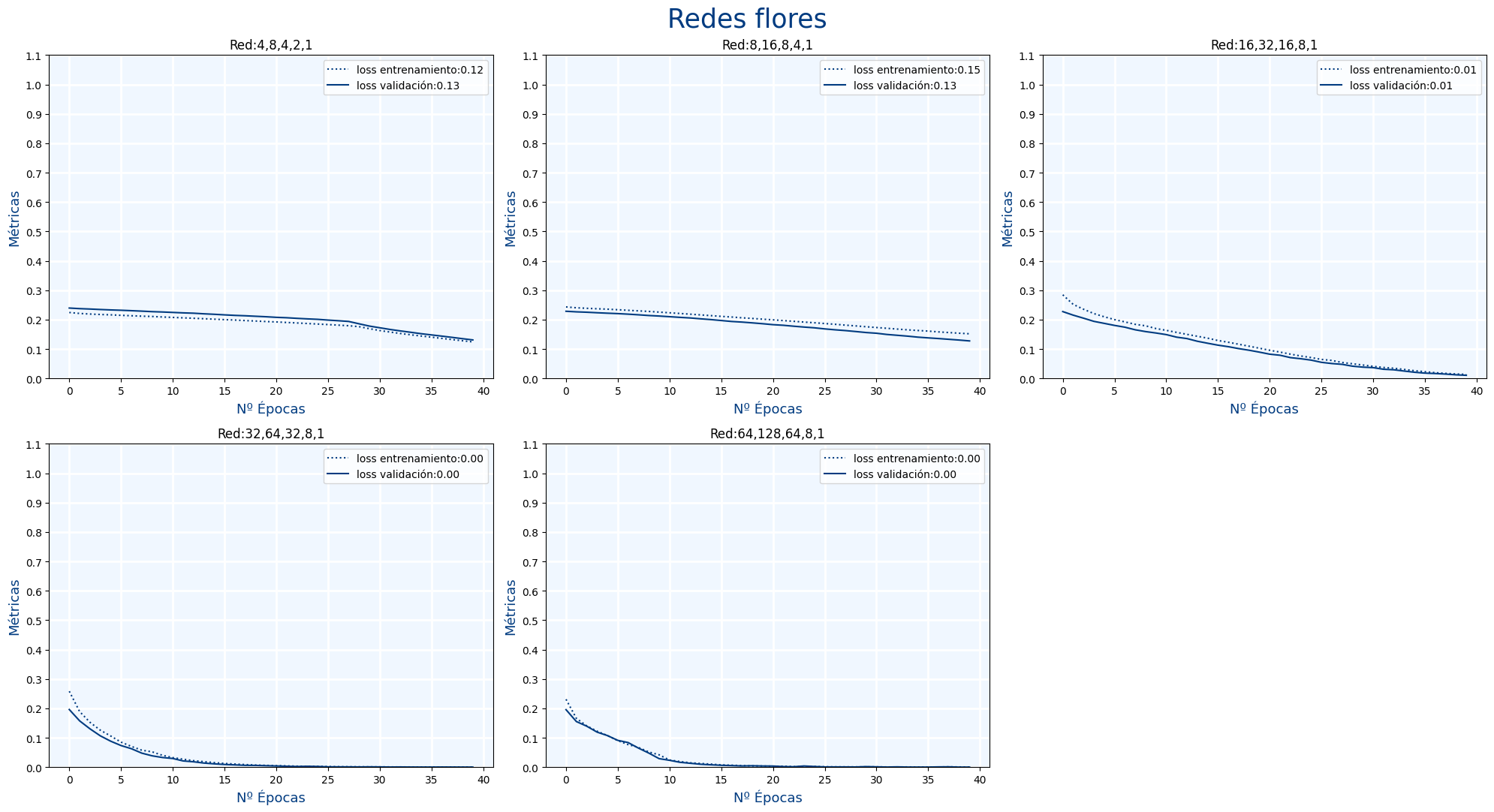
Ejercicio 23.D
Repite el ejercicio anterior pero ahora divide los datos en entrenamiento y validación.
Para ello usa la función train_test_split de sklearn
1 2 3 |
from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42) |
El parámetro test_size indica el % de datos (en tpu) que serán para el test.
Ahora deberás indicar en el método fit que ahora hay datos de entrenamiento y de test
1 |
history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=epochs,verbose=False) |
Para acabar ahora están las métricas de:
loss: La pérdida en entrenamientoval_loss: La pérdida en validación
Al mostrar la gráfica, muestra tanto loss como val_loss del mismo color pero que la línea de val_loss sea continua y la línea de val_loss sea puenteada
Mini-proyecto
Paso 1
De varios paises tenemos los siguientes datos del gatos en educación y su PIB que nos retorna la función get_datos:
1 2 3 4 5 6 7 8 9 10 11 12 |
def get_datos(): datos=np.array( [[ 2.01666708 , 56.18031474], [ 4.79734083 , 47.18848199], [ 9.23784581 , 57.68974048], [ 14.11529384 , 43.70348368], [ 14.92688637 , 59.10244323], [ 17.34408196 , 65.96080804], [ 17.62435324 , 45.74334603], [ 22.41875021 , 13.575581 ], [ 25.3139145 , 68.43756969], [ 34.85886672 , 147.15375307], [ 38.87476262 , 25.39687009], [ 42.01380169 , 74.39010069], [ 46.63551059 , 98.93395801], [ 49.58578273 , 116.07013679], [ 50.18371003 , 138.55546747], [ 52.06630172 , 139.36601894], [ 54.68810274 , 150.09622546], [ 57.13046193 , 156.14375739], [ 66.35609935 , 119.75844452], [ 69.05499042 , 139.08155228], [ 69.51252436 , 128.72247348], [ 69.83788756 , 152.65110462], [ 79.76649746 , 148.23106977], [ 81.83730552 , 137.86314926], [ 87.09879038 , 217.28932067], [ 89.00469759 , 168.64994509], [ 93.17139213 , 163.10598352], [ 93.66070686 , 200.47638924], [ 94.1944751 , 150.44019156], [ 97.36920633 , 173.2055957 ]]) return datos |
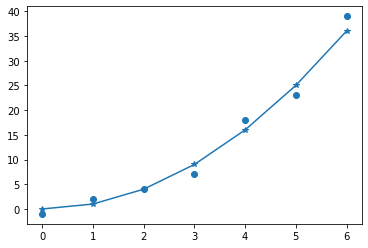
Crea la siguiente gráfica:
Paso 2
Resulta que la ecuación correcta que rige ese modelo es una recta:
y=a⋅x+b
pib=a⋅gastoseneducacion+b
y sabiendo
a=1.6b=30
pib=1.6⋅gastoseneducacion+30
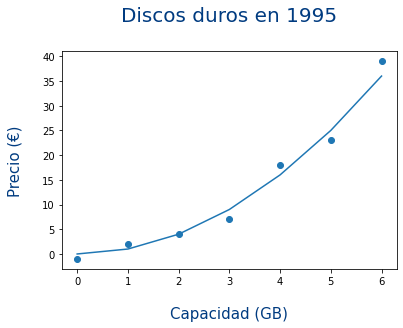
Muestra ahora esa ecuación sobre el gráfico anterior.
Paso 3
Ahora usando la siguiente red neuronal:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
def compile_fit(x,y,epochs): np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() model.add(Dense(1,input_dim=1)) model.compile(loss='mean_squared_error') history=model.fit(x, y,verbose=False,epochs=epochs) return model,history |
- Entrena la red neuronal durante 200 épocas
- Muestra el resultado de la red neuronal sobre la gráfica anterior usando el método
model.predict() - Muestra el valor de a y b del modelo con las siguientes líneas
1 2 |
a_pred=model.layers[0].get_weights()[0][0,0]b_pred=model.layers[0].get_weights()[1][0] |
Paso 4
Vuelve a entrenar ahora el modelo ahora con 27500 épocas y comprueba ahora da mejores resultados.
Para ello:
- Vuelve a recrear la gráfica anterior
- Muestra los valores de a y b
Paso 5
Ahora vamos a calcular como de "buena" es nuestra red. Para ellos vamos a calcular "Perdida" o "Loss" de la red neuronal.
La formula que vamos a usar es Mean Squared Error (MSE)
loss=Perdida=errormedio=1NN∑i=1|ytrue−yscore|2=1NN∑i=1|pibtrue−pibpredicho|2
Imprime el resultado
Paso 6
Si nos fijamos cuando hemos definido la red neuronal , el método model.compile hemos usado el argumento loss='mean_squared_error'
1 |
model.compile(loss='mean_squared_error') |
Es decir que le estamos diciendo a la red neuronal que para entrenarse use el Mean Squared Error como función de pérdida.
Así que resulta que no hace falta que nosotros calculemos el Mean Squared Error porque ya lo hace keras por nosotros.
La forma de acceder a ese valor es la siguiente, el método model.fit() nos retorna un objeto history que contiene las pérdidas al inicio de cada época. Y podemos acceder al array de todas las pérdidas (una por época) mediante history.history['loss']
1 |
history=model.fit(x, y,verbose=False, epochs=epochs) |
1 |
loss=history.history['loss'] |
En este caso loss es un array con la pérdida en cada época. Imprime el valor de la pérdida de la última época y comparalo con el resultado del paso anterior.
Paso 7
Ahora muestra una gráfica con todos los valores de loss para que veas como va evolucionando la pérdida a medida que se va entrenando la red en cada época Y muestra la última perdida
Paso 8
Paso 9
Ahora vamos a crear una red neuronal muchísimo más compleja para hacer que el error sea aun menor. La red es la siguiente:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
def compile_fit(x,y,epochs): np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() model.add(Dense(1,activation="relu",input_dim=1)) model.add(Dense(10,activation="relu")) model.add(Dense(100,activation="relu")) model.add(Dense(300,activation="relu")) model.add(Dense(600,activation="relu")) model.add(Dense(900,activation="relu")) model.add(Dense(1800,activation="relu")) model.add(Dense(900,activation="relu")) model.add(Dense(600,activation="relu")) model.add(Dense(300,activation="relu")) model.add(Dense(200,activation="relu")) model.add(Dense(100,activation="relu")) model.add(Dense(10,activation="relu")) model.add(Dense(1,input_dim=1)) model.compile(loss='mean_squared_error',optimizer="Adam") history=model.fit(x, y,verbose=False, epochs=epochs) return model,history |
Entranala durante 10000 épocas y muestra las 2 gráficas
Paso 10
Ahora usando los siguientes datos, calcula manualmente la pérdida loss y comparala con la pérdida anterior
1 2 3 4 5 6 7 8 9 10 11 |
def get_datos_validacion(): datos_validacion=np.array( [[ 1.22140488 , 59.35315077] , [ 2.42834632 , 3.50613409] , [ 4.27529991 , 70.39938914] , [ 14.44651349 , 50.0606769 ] , [ 16.10795855 , 81.08562061] , [ 16.75024181 , 33.95365822] , [ 26.80487149 , 47.1495392 ] , [ 28.81517859 ,106.34919698] , [ 48.56698654 ,120.25398606] , [ 52.08015067 ,116.7993955 ] , [ 53.30646055 ,131.30936472] , [ 55.09968806 ,131.34281752] , [ 60.39615207 , 97.77483743] , [ 73.52487026 , 92.30645543] , [ 76.2771471 ,109.9995226 ] , [ 84.56808303 ,120.60657657] , [ 89.2700557 ,117.3687155 ] , [ 91.03720679 ,159.47376137] , [ 93.53406333 ,166.44439331] , [ 94.78103495 ,180.66942656]] ) return datos_validacion |
Añade a la gráfica los datos de validación
¿Que ha ocurrido? Se llama Sobreajuste
Paso 11
Estos nuevos datos se pueden incluir también en el método model.fit para que nos calcule la pérdida con los datos de validación en cada época. Para ello modificaremos el método model.fit añadiendo el argumento validation_data=(x_val,y_val):
1 |
history=model.fit(x, y,validation_data=(x_val,y_val), verbose=False, epochs=epochs) |
Para acceder desde history a la pérdida en validación se usará:
1 |
val_loss=history.history['val_loss'] |
Muestra ahora una nueva figura con la perdida tanto en entrenamiento como en validación y los datos.
Paso 12
Paso 13
Ahora vamos a hacer predicciones en el modelo y comprobar si hay algún problema a lo largo del tiempo. Para ello vamos a realizar 300 predicciones semanales y obtener la media y la desviación estándar de todas las predicciones de una semana. Y eso lo vamos a realizar durante 600 semanas.
Para obtener las 300 predicciones semanales vamos a usar la siguiente función get_gastos_educacion():
1 2 3 4 5 6 7 |
np.random.seed(8)def get_gastos_educacion(semana): num_predicciones_semanales=300 gastos_educacion=np.random.uniform((semana/np.random.uniform(20,30)),30+(semana/np.random.uniform(5,20))-np.random.uniform(1,20),num_predicciones_semanales) gastos_educacion=gastos_educacion[gastos_educacion>1] return gastos_educacion |
Y mostraremos para cada un de las 600 semanas la media y la desviación estandard.
¿Ves algo raro?
Paso 14
Siguiendo con el DataSet de los precios de viviendas en la ciudad de Boston, vamos a mostrar las gráficas con las pérdidas y la métrica del Coeficiente de determinación o R² de todas las redes neuronales que se entrenaron en el tema anterior (entrenamiento y validación)
Para poder mostrar el Coeficiente de determinación o R² deberemos modificar el método model.compile de la siguiente forma:
1 |
model.compile(loss='mean_squared_error',metrics=[tf.keras.metrics.R2Score()]) |
Se usa de la siguiente forma:
- Obtener el R² para cada época en el entrenamiento
1 |
r2_score=history.history['r2_score'] |
- Obtener el R² para cada época en validación
1 |
r2_score_validacion=history.history['val_r2_score'] |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
redes_neuronales=[ [[20,1],"relu"], [[20,1],"selu"], [[20,1],"tanh"], [[20,10,1],"relu"], [[20,10,1],"selu"], [[20,10,1],"tanh"], [[20,30,10,1],"relu"], [[20,30,10,1],"selu"], [[20,30,10,1],"tanh"], [[20,40,80,40,20,1],"relu"], [[20,40,80,40,20,1],"selu"], [[20,40,80,40,20,1],"tanh"], [[20,40,80,160,80,40,20,1],"relu"], [[20,40,80,160,80,40,20,1],"selu"], [[20,40,80,160,80,40,20,1],"tanh"] ] epochs=300 |
Nombre Capas Épocas Activación MSE R² Tiempo MSE R²
Red Entrenamiento Entrenamiento Entrenamiento Validación Validación
-------- -------------------------------- -------- ------------ --------------- --------------- --------------- ------------ ------------
1 [20, 1] 300 relu 25.9903 0.700825 13.2181 24.1596 0.670553
2 [20, 1] 300 selu 23.1742 0.733241 12.6924 21.8751 0.701705
3 [20, 1] 300 tanh 69.747 0.197143 12.3714 61.0294 0.167786
4 [20, 10, 1] 300 relu 24.5118 0.717845 12.8602 26.5133 0.638458
5 [20, 10, 1] 300 selu 23.5015 0.729474 12.4664 23.3333 0.681821
6 [20, 10, 1] 300 tanh 59.5199 0.314867 12.466 51.4849 0.297938
7 [20, 30, 10, 1] 300 relu 13.5217 0.844352 13.0145 17.7428 0.758054
8 [20, 30, 10, 1] 300 selu 11.4235 0.868504 12.895 16.8747 0.769892
9 [20, 30, 10, 1] 300 tanh 59.6715 0.313121 12.7907 50.0339 0.317724
10 [20, 40, 80, 40, 20, 1] 300 relu 11.639 0.866023 13.8727 15.3683 0.790433
11 [20, 40, 80, 40, 20, 1] 300 selu 19.7779 0.772336 13.6373 26.7263 0.635553
12 [20, 40, 80, 40, 20, 1] 300 tanh 55.5066 0.361063 13.6796 50.5201 0.311094
13 [20, 40, 80, 160, 80, 40, 20, 1] 300 relu 22.3828 0.742352 13.9058 27.3831 0.626596
14 [20, 40, 80, 160, 80, 40, 20, 1] 300 selu 6.17364 0.928935 14.0711 17.3759 0.763057
15 [20, 40, 80, 160, 80, 40, 20, 1] 300 tanh 86.8736 -2.5034e-06 14.0382 75.0856 -0.0238888
Para cada una de las redes indica:
- Si tiene unas buenas métricas en la última época
- Si es buena o mala red , es decir si la elegirías. Explica el motivo
- Compara los resultados con los del tema anterior ¿Porque hay esas variaciones?