Herramientas de usuario
Barra lateral
Tabla de Contenidos
1. Introducción a las redes neuronales
Es este tema vamos a ver un ejemplo concreto de una red neuronal.
Definición del problema
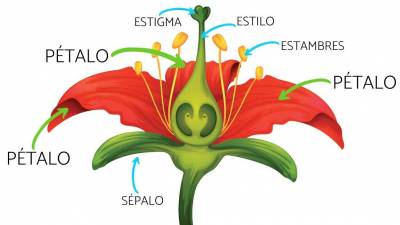
Vamos a ver un ejemplo muy sencillo de red neuronal que averigüe el tipo de una flor. Para ello vamos a usar un conjunto de datos que se llaman el Conjunto de datos flor iris.
Para ello vamos a usar las siguientes variables de entrada:
- El largo de su sépalo: Medido en cm
- El largo de su pétalo: Medido en cm
Este conjunto de datos pretende distinguir entre los siguientes dos tipos de flores:
- Setosa
- Versicolor
Veamos ahora algunos datos:
| X | Y | |
| Largo Sépalo | Largo Pétalo | Tipo de Flor |
| 5.1 | 1.4 | Setosa |
| 4.9 | 1.4 | Setosa |
| 4.7 | 1.3 | Setosa |
| 4.6 | 1.5 | Setosa |
| 5.0 | 1.4 | Setosa |
| 5.4 | 1.7 | Setosa |
| 5.1 | 1.9 | Setosa |
| 4.8 | 1.4 | Setosa |
| 5.3 | 1.5 | Setosa |
| 5.0 | 1.4 | Setosa |
| 7.0 | 4.7 | Versicolor |
| 6.4 | 4.5 | Versicolor |
| 6.9 | 4.9 | Versicolor |
| 5.5 | 4.0 | Versicolor |
| 6.2 | 4.5 | Versicolor |
| 5.6 | 3.9 | Versicolor |
| 5.9 | 4.8 | Versicolor |
| 6.1 | 4.0 | Versicolor |
| 6.3 | 4.9 | Versicolor |
| 6.3 | 4.4 | Versicolor |
| 5.6 | 4.1 | Versicolor |
| 5.7 | 4.2 | Versicolor |
| 5.7 | 4.2 | Versicolor |
| 6.2 | 4.3 | Versicolor |
| 5.1 | 3.0 | Versicolor |
- El largo de su sépalo
- El largo de su pétalo
- El ancho de su sépalo
- El ancho de su pétalo
Y distingue entre 3 tipos de flores:
- Setosa
- Versicolor
- Virginica
Pero por simplificar hemos usado solo el largo del sépalo y pétalo y dos tipos de flores.
La red neuronal lo único que va a hacer es "aprender" a crear una función matemática que dado el largo del sépalo y el largo del pétalo calcule el tipo de flor:
$$ tipo \: flor=f(largo \: sépalo,largo \: pétalo) $$
- 0:Setosa
- 1:Versicolor
La red neuronal
Vamos a hacer la siguiente red neuronal:
Esta red neuronal, consta de una serie de neuronas (ya contaremos mas adelante que es una neurona) que se pasan valores de unas a otras. Son cada uno de los círculos. Las neuronas se organiza en capas:
- Capa de entrada (Círculos amarillos): Es una única capa por donde entran los datos de entrada. Es decir los valores del largo del sépalo y el largo del pétalo. Por lo tanto en este caso debe haber 2 neuronas , una por cada valor de entrada.
- Capas ocultas (Círculos verdes): Son varias capas, las cuales calculan de que tipo es cada flor. La primera capa oculta consta de 6 neuronas. La segunda capa oculta consta de 12 neuronas . La última capa oculta consta de 6 neuronas.
- Capa de salida (Círculos rojos): Es una única capa que es la que genera el resultado de la red neuronal. Como la red genera un único número la capa tiene solo 1 neurona.
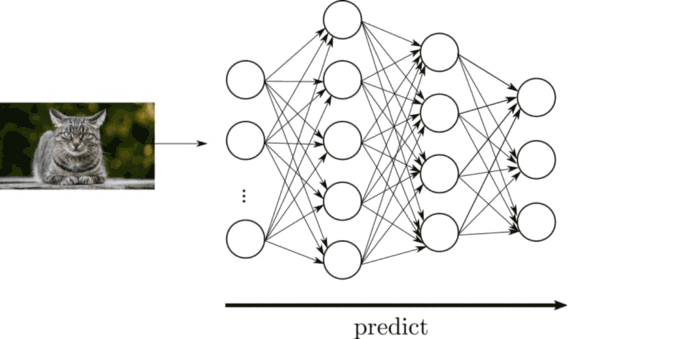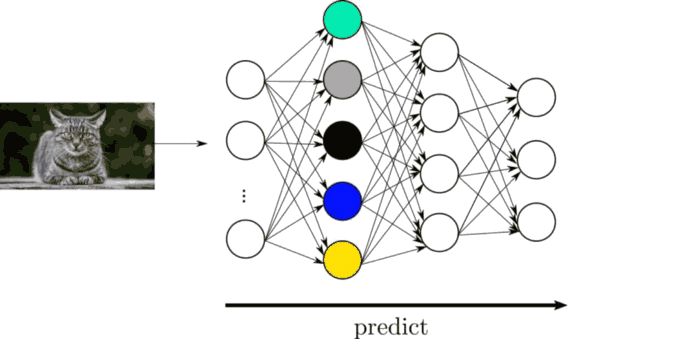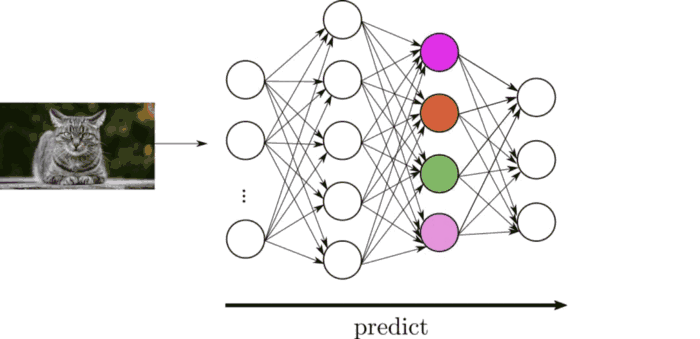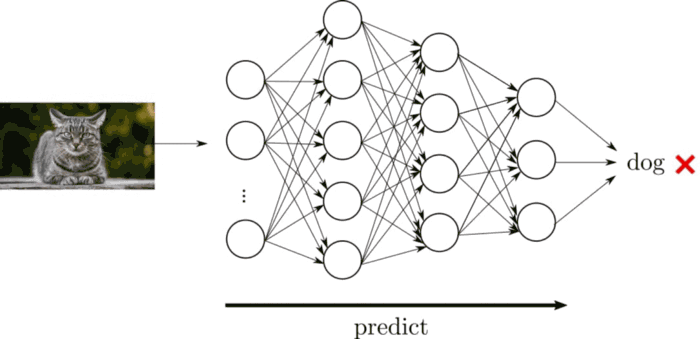
La siguiente imagen es una animación de una red neuronal que calcula si una foto es un perro:
Google Colaboratory
Google Colaboratory es un IDE para programar en Python. El formato del IDE sige lo que se llaman "Jupyter Notebooks" que son ficheros con extensión "ipynb". Estos ficheros se pueden abrir desde VS Code u otros IDEs.
Ves a la página de Google Colaboratory, pincha en "Nuevo Cuaderno" y ya puedes empezar a programar en Python.
Una explicación completa de Google Colab la puedes ver en video Introducción a Google Colab, una noble y completa guía.
Código en Python
Veamos ahora el código python de la red neuronal.
El código completo es el siguiente:
import numpy as np import pandas as pd import tensorflow as tf import matplotlib.pyplot as plt from keras.models import Sequential from keras.layers import Dense from sklearn.datasets import load_iris from matplotlib.colors import LightSource import random iris=load_iris() sepal_length=iris.data[0:99,0] petal_length=iris.data[0:99,2] flower_type=iris.target[0:99] x=np.column_stack((sepal_length,petal_length)) y=flower_type np.random.seed(5) tf.random.set_seed(5) random.seed(5) model=Sequential() model.add(Dense(6, activation='relu',input_dim=2)) model.add(Dense(12, activation='relu')) model.add(Dense(6, activation='relu')) model.add(Dense(1, activation='sigmoid')) model.compile(loss='mean_squared_error') model.fit(x, y,epochs=40) print(model.predict([[4.9,1.4]])) print(model.predict([[6.3,4.9]]))
Ahora vamos a ver todo el código paso a paso.
import numpy as np import pandas as pd import tensorflow as tf import matplotlib.pyplot as plt from keras.models import Sequential from keras.layers import Dense from sklearn.datasets import load_iris from matplotlib.colors import LightSource
Estas líneas simplemente hacer los "import" de varias cosas que vamos a usar.
iris=load_iris() sepal_length=iris.data[0:99,0] petal_length=iris.data[0:99,2] flower_type=iris.target[0:99] x=np.column_stack((sepal_length,petal_length)) y=flower_type
Hemos cargado los datos y hemos creado 3 arrays:
sepal_length: Con la longitud de cada sépalo que es la columna 0 de la matrizdatapetal_length: Con la longitud de cada pétalo que es la columna 2 de la matrizdataflower_type: Con el tipo de flor (0 o 1)
Luego hemos creado una matriz juntando la longitud de cada sépalo y la longitud de cada pétalo, es lo que llamaremos x y luego hemos creado la y que es el tipo de flor.
Es decir que vamos a entrenar a red neuronal con los valores de x e y para que cree la función matemática capaz de calcular el tipo de flor en función de las longitudes.
np.random.seed(5) tf.random.set_seed(5) random.seed(5)
Para a siempre nos salgan los mismos resultados, hemos inicializado los generadores de números aleatorios.
model=Sequential() model.add(Dense(6, activation='relu',input_dim=2)) model.add(Dense(12, activation='relu')) model.add(Dense(6, activation='relu')) model.add(Dense(1, activation='sigmoid')) model.compile(loss='mean_squared_error')
Hemos creado el la estructura de la red neuronal. Excepto la capa de entrada, cada capa se especifica por un objeto de tipo Dense y el primer número especifica el Nº de neuronas de esa capa.
En la primera capa también hemos indicado la propiedad input_dim con el valor 2 que indica el Nº de valores de entrada , es decir que estamos diciendo el tamaño de la capa de entrada.
loss.
Para acabar compilamos el modelo con el método compile.
model.fit(x, y,epochs=40)
Ahora vemos a entrenar con el método fit la red neuronal para que ella internamente genere la función matemática. Fíjate como le pasamos la matriz con los datos de entrada x y el vector con el resultado que debe dar y.
Por último le decimos cuantas veces tiene que entrenar la red con el parámetro epochs. Cuanto más lo entrenemos , en general mejor será la red (Esta frase tiene muchos matices pero ya lo iremos viendo a lo largo del curso).
Epoch 1/40 4/4 [==============================] - 1s 9ms/step - loss: 0.2036 Epoch 2/40 4/4 [==============================] - 0s 5ms/step - loss: 0.1879 Epoch 3/40 4/4 [==============================] - 0s 5ms/step - loss: 0.1885 Epoch 4/40 4/4 [==============================] - 0s 3ms/step - loss: 0.1734 Epoch 5/40 4/4 [==============================] - 0s 7ms/step - loss: 0.1743 ................ Epoch 35/40 4/4 [==============================] - 0s 3ms/step - loss: 0.0110 Epoch 36/40 4/4 [==============================] - 0s 3ms/step - loss: 0.0101 Epoch 37/40 4/4 [==============================] - 0s 3ms/step - loss: 0.0085 Epoch 38/40 4/4 [==============================] - 0s 3ms/step - loss: 0.0085 Epoch 39/40 4/4 [==============================] - 0s 2ms/step - loss: 0.0070 Epoch 40/40 4/4 [==============================] - 0s 6ms/step - loss: 0.0066
Ahora vemos el resultado del entrenamiento para cada una de las épocas, fíjate en loss , es lo que nos dice como de buena es nuestra red. Cuanto más pequeño sea ese valor, mejor es la red.
print(model.predict([[4.9,1.4]])) print(model.predict([[6.3,4.9]]))
Una vez acabar vamos a usar nuestra función matemática con el método predict con los siguientes valores:
| X | Y | |
| Largo Sépalo | Largo Pétalo | Tipo de Flor |
| 4.9 | 1.4 | Setosa |
| 6.3 | 4.9 | Versicolor |
[[0.06094426]] [[0.9634158]]
Vemos como los resultados no son exactamente 0 o 1 sino número cercanos como el 0.0609 o el 0.9634158 pero no nos preocupemos, las redes neuronales no suelen dar resultados exactos al 100%.
- TensorFlow: Es una librería de Google. El problema es que es de muy bajo nivel. Fue de las primeras.
- Keras: Es un API que está por encima de TensorFlow haciendo que sea muy sencillo crear redes neuronales.
- Pytorch: Es la alternativa a Keras, está hecha por Facebook. Se usa mucho en proyectos de investigación.
Durante el curso vamos a usar Keras y algo de TensorFlow
Gráficas
La mayoría de veces para una mayor comprensión de los datos queremos también ver gráficos de éstos.
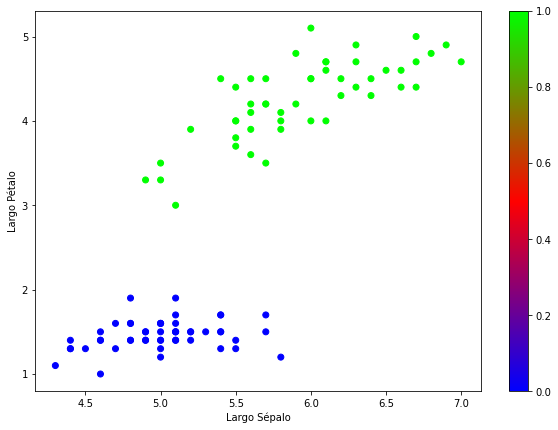
El siguiente código Python muestra la siguiente gráfica con cada una de las flores de los datos.
figure=plt.figure(figsize = (10, 7))
axes = figure.add_subplot()
scatter=axes.scatter(x=x[:,0], y=x[:,1], c=y, cmap=plt.cm.brg)
figure.colorbar(scatter,ax=axes)
axes.set_xlabel('Largo Sépalo')
axes.set_ylabel('Largo Pétalo')
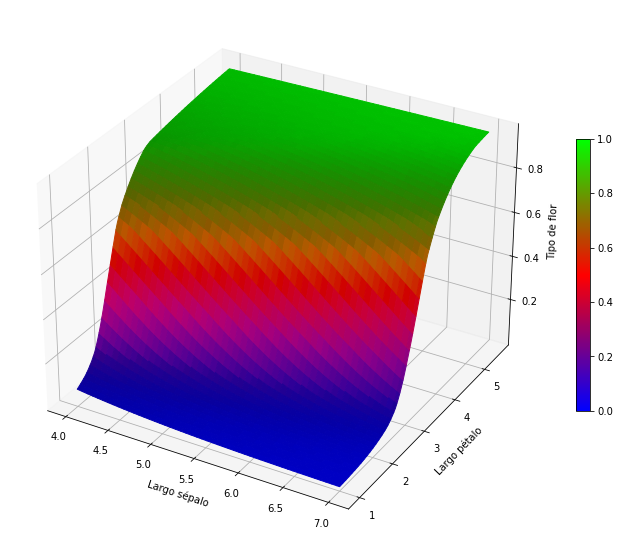
Ahora vamos a hacer una gráfica con el resultado de la red neuronal
figure=plt.figure(figsize=(8,8))
axes = figure.add_subplot(projection='3d')
xt=np.linspace(4,7,100)
yt=np.linspace(1,5.5,100)
xt,yt=np.meshgrid(xt,yt)
xa=xt.reshape(-1)
ya=yt.reshape(-1)
xya=np.column_stack((xa,ya))
za=model.predict([xya])
zt=np.reshape(za,xt.shape)
light_source = LightSource()
facecolors = light_source.shade(zt,plt.cm.brg, blend_mode='soft')
surface=axes.plot_surface(xt,yt,zt,facecolors=facecolors)
figure.colorbar(plt.cm.ScalarMappable(cmap=plt.cm.brg),ax=axes, shrink = 0.5)
axes.set_xlabel('Largo sépalo')
axes.set_ylabel('Largo pétalo')
axes.set_zlabel('Tipo de flor')
Lo que hay que hacer es comparar los datos de las 2 gráficas para si son coherentes entre ellas. Y obviamente lo son
Ejercicios
Ejercicio 1
Usando Google collab haz una red neuronal en python con Keras que obtenga el tipo de flor en función del "Largo Sépalo" y de "Largo Pétalo".
Obtén el resultado de la red neuronal para las siguientes entradas e indica el tipo de flor que ha calcula la red neuronal.
| Largo Sépalo | Largo Pétalo | Resultado red neuronal | Tipo de Flor(0 o 1) |
| 5.4 | 1.7 | ||
| 5.5 | 4.0 |
Ejercicio 2
Modifica ahora la red neuronal de forma que:
- La 1º capa oculta tenga 4 neuronas en vez de 6
- La 2º capa oculta tenga 6 neuronas en vez de 12
- La 3º capa oculta tenga 4 neuronas en vez de 6
- La 4º capa seguirá teniendo 1 neurona
Usando la web http://alexlenail.me/NN-SVG/index.html dibuja la red neuronal que acabas de crear
Ahora muestra los resultados
| Largo Sépalo | Largo Pétalo | Resultado red neuronal | Tipo de Flor(0 o 1) |
| 5.4 | 1.7 | ||
| 5.5 | 4.0 |
Ejercicio 3
Usando el código de la red original, modifica las siguientes líneas:
sepal_length=iris.data[0:99,0] petal_length=iris.data[0:99,2] flower_type=iris.target[0:99]
de forma que queden así:
sepal_length=iris.data[:,0] petal_length=iris.data[:,2] flower_type=iris.target[:]
Entrena la red con los nuevos datos
Muestra la gráfica con los datos de entrada usando el código:
figure=plt.figure(figsize = (10, 7))
axes = figure.add_subplot()
scatter=axes.scatter(x=x[:,0], y=x[:,1], c=y, cmap=plt.cm.brg)
figure.colorbar(scatter,ax=axes)
axes.set_xlabel('Largo Sépalo')
axes.set_ylabel('Largo Pétalo')
Ahora verás que hay otro tipo de flor llamado Virginica.
Prueba a ver si funciona ahora la red neuronal con el nuevo tipo de flor.
| Largo Sépalo | Largo Pétalo | Resultado red neuronal | Tipo de Flor |
| 6.9 | 5.1 | ||
| 7.7 | 6.1 |
Ejercicio 4
Piensa al menos 3 problemas que se podrían resolver con una red neuronal similar a la que has usado.
Ejercicio 5
Vamos a ver ahora otro conjunto de datos relativo a la detección de cáncer de mama.
Los datos se obtienen de la siguiente forma:
from sklearn.datasets import load_breast_cancer breast_cancer=load_breast_cancer() x=breast_cancer.data y=breast_cancer.target
Este conjunto de datos tiene 30 variable de entrada, que son las siguentes:
- mean radius
- mean texture
- mean perimeter
- mean area
- mean smoothness
- mean compactness
- mean concavity
- mean concave points
- mean symmetry
- mean fractal dimension
- radius error
- texture error
- perimeter error
- area error
- smoothness error
- compactness error
- concavity error
- concave points error
- symmetry error
- fractal dimension error
- worst radius
- worst texture
- worst perimeter
- worst area
- worst smoothness
- worst compactness
- worst concavity
- worst concave points
- worst symmetry
- worst fractal dimension
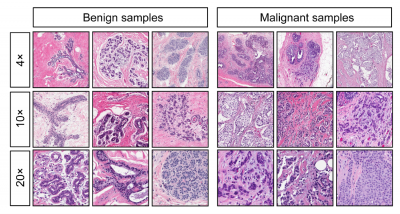
Esto datos son relativos a imágenes de núcleos celulares como los siguientes:
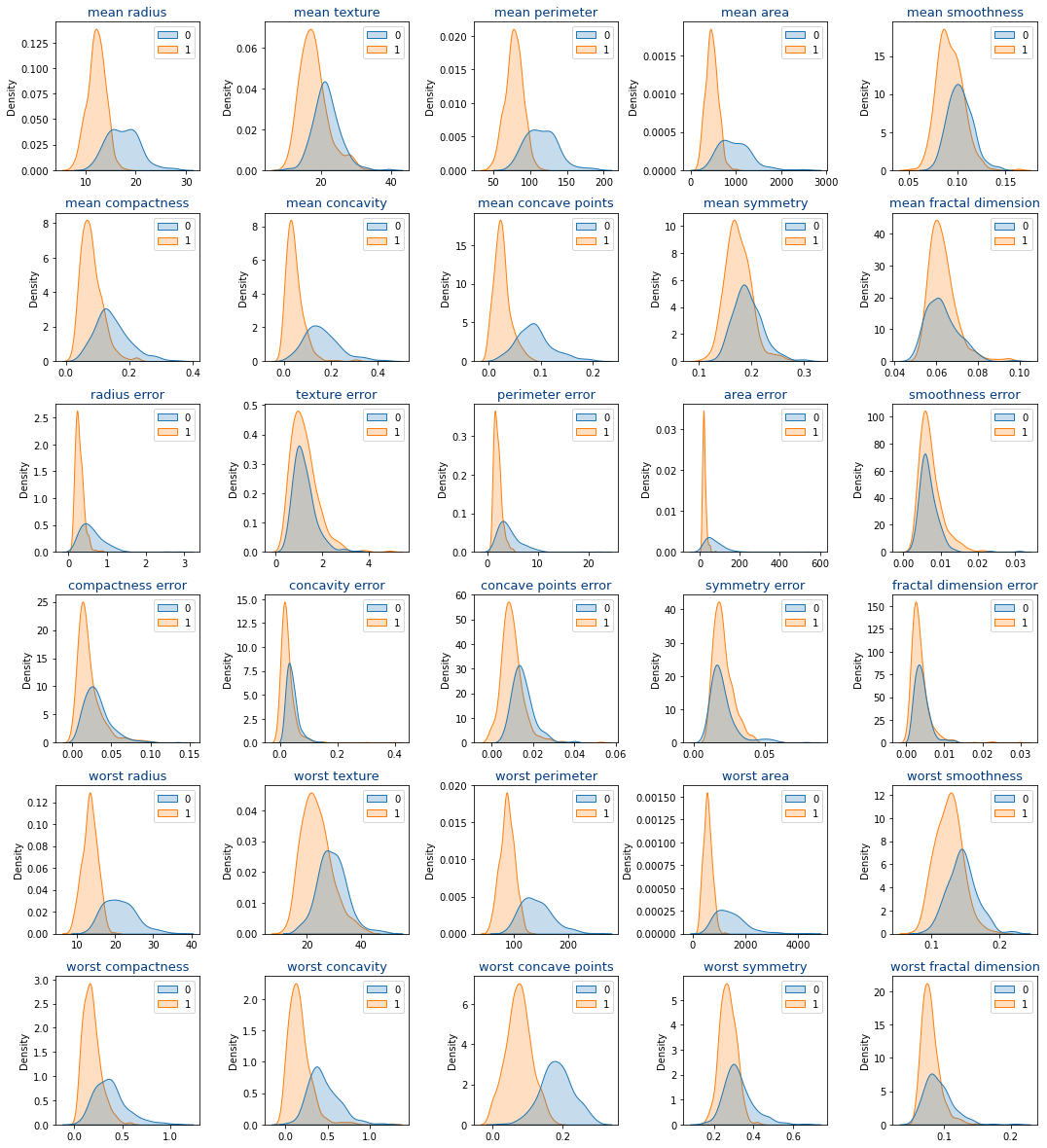
Y los histogramas de todos los datos son los siguientes:
Podemos ven en los histogramas que no hay una forma fácil de saber si una célula es o no cancerígena.
Imprime el valor de la fila 56 tanto de la x como de la y.
#Para que los datos no se muestren con notación científica np.set_printoptions(suppress=True) print(x[56],y[56])
Ahora muestra los valores de la x y la y para la fila 204.
Crea una red neuronal en las que en cada capa tenga los siguientes números de neuronas:
| Nº Capa | Nº Neuronas |
| 1º | 30 |
| 2º | 60 |
| 3º | 100 |
| 4º | 60 |
| 5º | 30 |
| 6º | 10 |
| 7º | 1 |
Rellena la siguiente tabla y muestrala
| Fila Datos | Resultado verdadero | Resultado red neuronal |
| 56 | ||
| 204 |
¿Es una buena red?
Usa hora una red más pequeña de forma que tenga las siguientes capas:
| Nº Capa | Nº Neuronas |
| 1º | 6 |
| 2º | 12 |
| 3º | 6 |
| 4º | 1 |
Rellena la siguiente tabla y muestrala
| Fila Datos | Resultado verdadero | Resultado red neuronal |
| 56 | ||
| 204 |
¿Es una buena red?
Ejercicio 6
Repite la red pequeña del ejercicio anterior pero ahora modificando la semilla de los números aleatorios
np.random.seed(5) tf.random.set_seed(5) random.seed(5)
Rellena la siguiente tabla y muestrala con una red con la semilla 6
| Fila Datos | Resultado verdadero | Resultado red neuronal |
| 56 | ||
| 204 |
Rellena la siguiente tabla y muestrala con una red con la semilla 88
| Fila Datos | Resultado verdadero | Resultado red neuronal |
| 56 | ||
| 204 |