Tabla de Contenidos

8 Métricas y Evaluación de redes neuronales

Hasta ahora hemos visto como definir una red neuronal y como entrenarla. El último paso que nos queda es saber si la red ha funcionado correctamente. Pero ¿Eso no se hacía con la función de coste? Pues no exactamente. La función de coste se usa para ayudar a ajustar los parámetros durante el entrenamiento mediante los datos de entrada pero no para saber si el modelo es bueno. Para saber si el modelo es bueno , se usan las métricas.

Hay métricas que son las mismas que las funciones de coste pero hay otras métricas que no existen como función de coste.

Las métricas son un tema del que se habla mucho pero no se termina de explicar bien. Debido a que tienen una mínima parte de estadística se suelen contar de forma muy superficial y desde mi punto de vista hasta se explican de forma erronea.

Puesto que el tema de las métricas es muy extenso ya que hay muchísimas métricas, lo hemos dividido en:

Métricas en keras

En el método fit de Keras tenemos un nuevo parámetro para indicar la métrica llamado metrics que contiene un array con todas las métricas que queremos tener en nuestra red mientras se va entrenando 

model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.SGD(learning_rate=0.01),metrics=["AUC"])
history=model.fit(x,y_true,epochs=20,verbose=False)


history.history['auc']


history.history['val_auc']

Validación

Acabamos de ver que entrenando la red neuronal , el error se consigue bajar a prácticamente cero. Es decir que los valores de los parámetros , pesos (weight) y sesgos bias, debe ser muy buenos. No exactamente. Resulta que los parámetros se han ajustado a los datos que le hemos pasado, pero ¿Como es de bueno el modelo para nuevos datos que no ha visto? Realmente ver como se comporta con datos nuevos y con los datos que ha ya visto es lo que nos va a decir como es de bueno nuestro modelo. Así que pasemos a ver como sacar las métricas también con datos nuevos.

Lo primero es averiguar de donde obtenemos nuevos datos. Normalmente no tenemos nuevos datos así que lo que hacemos es que solo vamos a entrenar nuestra red neuronal con el 80% de los datos y el 20% restante los guardaremos para validar la red neuronal. Eso lo vamos a hacer con la función train_test_split de scikit-learn 

from sklearn.model_selection import train_test_split

x_train, x_test, y_train, y_test = train_test_split(x, y_true, test_size=0.2, random_state=42)

La función train_test_split tiene los siguientes argumentos:

Y ahora a Keras se los tenemos que pasar así: 

history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=epochs,verbose=False)

Lo datos de entrenamiento se pasan igual que antes pero los de validación se pasan en en un tupla en un parámetro llamado validation_data.

Por último tenemos que obtener la métrica para los datos de validación. Se obtiene igual que antes pero el nombre de la métrica empieza por val_ 

history.history['val_binary_accuracy']

Veamos un ejemplo completo: 

import numpy as np
import tensorflow as tf
import numpy as np
import pandas as pd
import keras
import random
from keras.models import Sequential
from keras.layers import Dense
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

iris=load_iris()
x=iris.data[0:99,2]
y_true=iris.target[0:99]

np.random.seed(5)
tf.random.set_seed(5)
random.seed(5)  

x_train, x_test, y_train, y_test = train_test_split(x, y_true, test_size=0.2, random_state=42)

model=Sequential()
model.add(Dense(3, input_dim=1,activation="sigmoid",kernel_initializer="glorot_normal"))
model.add(Dense(1,activation="sigmoid",kernel_initializer="glorot_normal"))
model.compile(loss="binary_crossentropy",optimizer=tf.keras.optimizers.Adam(learning_rate=0.01),metrics=["binary_accuracy"])
history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=40,verbose=False)

figure=plt.figure(figsize=(8,6))
axes = figure.add_subplot()

axes.plot(history.history['binary_accuracy'],label="Entrenamiento "+str(history.history['binary_accuracy'][-1]))
axes.plot(history.history['val_binary_accuracy'],label="Validación "+str(history.history['val_binary_accuracy'][-1]))

axes.legend()
axes.set_xlabel('Época', fontsize=15,labelpad=20,color="#003B80")  
axes.set_ylabel('Valor métrica', fontsize=15,labelpad=20,color="#003B80")
axes.set_facecolor("#F0F7FF")
axes.grid(b=True, which='major', axis='both',color="#FFFFFF",linewidth=1)

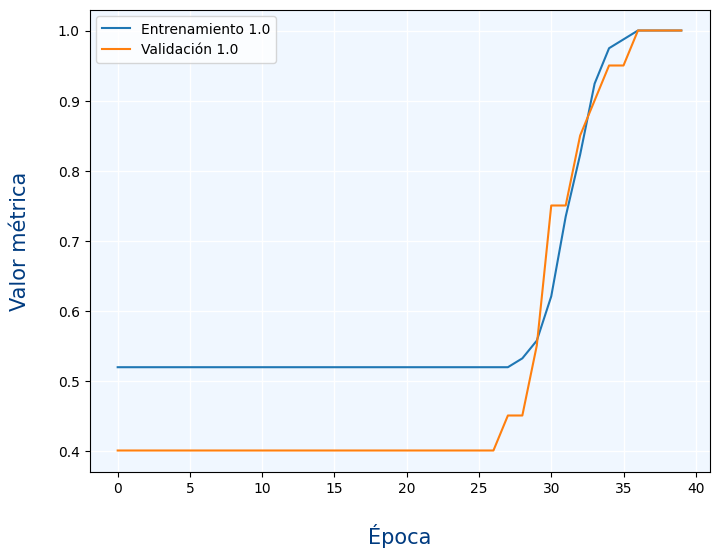
Podemos ver en el gráfico que la métrica es muy similar con los datos de validación que con los de entrenamiento. otro detalle importante es que las métricas suelen ser buenas si su valor es 1 (al contrario de las funciones de pérdida en la que lo bueno era un 0)

Ahora pasemos a ver las distintas métricas que hay:

Ejercicios

Ejercicio 1

Dado el problema de las flores, vuelve a entrenar una red neuronal pero ahora indicando los datos de validación.

Para ello deberás separar los datos en un 80% de datos para entrenamiento y un 20% de datos para validación

Muestra la gráfica en la que se vea el loss en cada época tanto en entrenamiento como en validación.

Ejercicio 2

Dado el problema de las imágenes de los números, vuelve a entrenar una red neuronal pero ahora indicando los datos de validación.

Para ello deberás separar los datos en un 80% de datos para entrenamiento y un 20% de datos para validación

Muestra la gráfica en la que se vea el loss en cada época tanto en entrenamiento como en validación.

Ejercicio 3

Repite los dos ejercicios anteriores pero ahora invirtiendo los porcentajes:

¿Como han cambiado las gráficas?