Tabla de Contenidos
6. Redes neuronales: Apendices
Inicialización de parámetros
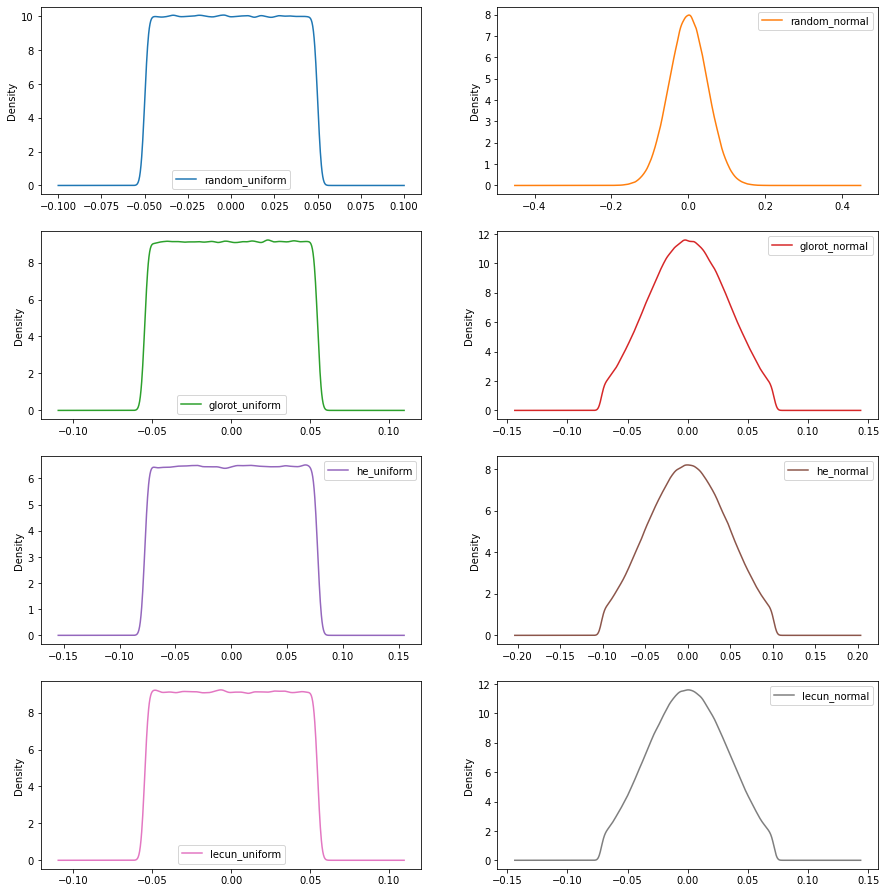
El siguiente código en Python nos muestra las funciones de distribución de cada uno de los inicializadores. El ejemplo no tiene utilidad real mas allá de mostrar los datos y las gráficas de los inicializadores.
import tensorflow as tf
import keras as keras
from keras.models import Sequential
from keras.layers import Dense
import pandas as pd
initializers=["random_uniform","random_normal","glorot_uniform","glorot_normal","he_uniform","he_normal","lecun_uniform","lecun_normal","zeros","ones"]
model=Sequential()
for initializer in initializers:
model.add(Dense(1000, input_dim=1000,kernel_initializer=initializer))
model.add(Dense(1000))
model.compile()
df=pd.DataFrame()
for index,initializer in enumerate(initializers):
pesos=(model.layers[index].get_weights()[0]).reshape(-1)
df[initializer]=pesos
df.describe()
df.iloc[:,0:8].plot(kind = 'density', subplots = True, layout = (5,2),figsize=(15,20),sharex = False)
random_uniform random_normal glorot_uniform glorot_normal he_uniform he_normal lecun_uniform lecun_normal zeros ones count 1000000.000000 1000000.000000 1000000.000000 1000000.000000 1000000.000000 1000000.000000 1000000.000000 1000000.000000 1000000.0 1000000.0 mean -0.000022 -0.000005 -0.000010 0.000020 0.000054 0.000019 -0.000008 -0.000040 0.0 1.0 std 0.028850 0.049970 0.031639 0.031590 0.044715 0.044714 0.031611 0.031635 0.0 0.0 min -0.050000 -0.238984 -0.054772 -0.071899 -0.077459 -0.101682 -0.054772 -0.071899 0.0 1.0 25% -0.025000 -0.033713 -0.027437 -0.022938 -0.038669 -0.032442 -0.027381 -0.023074 0.0 1.0 50% -0.000047 0.000047 -0.000014 0.000056 0.000099 0.000064 0.000006 -0.000038 0.0 1.0 75% 0.024980 0.033729 0.027406 0.022980 0.038725 0.032528 0.027364 0.022952 0.0 1.0 max 0.050000 0.232416 0.054772 0.071900 0.077460 0.101682 0.054772 0.071900 0.0 1.0
Ahora vamos a ver como se comportan 4 redes distintas según el número de capas, el inicializador y la función de activación usada
Mas información:
- Hyper-parameters in Action! Part II — Weight Initializers: Demostración sencilla de las fórmulas de Glorot y He.
- Kaiming He initialization: Demostración del inicializador He
- Artículos académicos originales sobre Glorot, He y LeCun:
- Understanding the difficulty of training deep feedforward neural networks: Artículo original de Xavier Glorot sobre su inicializador.
- Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification: Artículo original de Kaiming He sobre su inicializador.
- Efficient BackProp: Artículo original de Yann LeCun sobre su inicializador.
- Artículos académicos sobre la importancia de la inicialización en distintas redes:
Usando funciones de activación en Keras
Funciones personalizadas
Podemos crear nuestra propia función de activación
from tensorflow.keras import backend as K
def my_relu(x):
return K.maximum(0.3*x, x)
Y usarla de las siguientes formas
- Usando directamente la función de activación
model.add(Dense(3, input_dim=1,activation=my_relu))
- Creando una capa de activación en base a la función de activación con tf.keras.layers.Activation o tf.keras.layers.Lambda
model.add(Dense(3, input_dim=1)) model.add(Dense(3, input_dim=1,activation=tf.keras.layers.Activation(my_relu)))
model.add(Dense(3, input_dim=1)) model.add(Dense(3, input_dim=1,activation=tf.keras.layers.Lambda(my_relu)))
Funciones personalizadas parametrizadas
Pero si nuestra función tiene un parámetro
from tensorflow.keras import backend as K
def my_relu(x,alpha):
return K.maximum(alpha*x, x)
Solo podremos usar tf.keras.layers.Lambda
model.add(Dense(3, input_dim=1)) model.add(tf.keras.layers.Lambda(lambda x: my_relu(x,0.3)))
Funciones con nombre
Para acabar vamos a ver como poder usar el nombre en una capa que nos hayamos creado nosotros usando el método tf.keras.utils.get_custom_objects
Vamos a definir un nombre de función de activación llamado relu_0_3 usando get_custom_objects()
from tensorflow.keras import backend as K
from tensorflow.keras.utils import get_custom_objects
def my_relu(x,alpha):
return K.maximum(alpha*x, x)
get_custom_objects()['relu_0_3']=tf.keras.layers.Lambda(lambda x: my_relu(x,0.3))
Y simplemente lo usamos indicando el nombre de relu_0_3
model.add(Dense(3, input_dim=1,activation="relu_0_3"))
Tipos de funciones de activación en capas ocultas
sigmoid
La fórmula de la sigmoide se obtiene a partir de la función $logit$ o $log odds$.
$$odds(p) = \frac{p}{1-p} $$ $$logit(p) = log(odds(p))=log(\frac{p}{1-p}) $$
Ahora:
$$logit(p) = ax+b $$ $$log(\frac{p}{1-p}) = ax+b $$
Si despejamos $p$ de la anterior fórmula:
$$ log(\frac{p}{1-p}) = ax+b \\ e^{log(\frac{p}{1-p})} = e^{ax+b} \\ \frac{p}{1-p}=e^{ax+b} \\ p=e^{ax+b} \cdot (1-p) \\ p=e^{ax+b}-pe^{ax+b} \\ p+pe^{ax+b}=e^{ax+b} \\ p(1+e^{ax+b})=e^{ax+b} \\ p=\frac{e^{ax+b}}{1+e^{ax+b}} \\ p=\frac{ \frac{e^{ax+b}}{e^{ax+b}} }{ \frac{1+e^{ax+b}}{e^{ax+b}} } \\ p=\frac{ 1 }{ 1+\frac{1}{e^{ax+b}} } \\ p=\frac{ 1 }{ 1+e^{-(ax+b)} } \\ $$
Que es exactamente la función sigmoide
- Más información
ReLU y Leaky ReLU
Ahora vamos a complicarlo un poco. Resulta que la función de activación tf.keras.activations.relu tiene un parámetro llamado alpha que hace que comporte como la función Leaky ReLU. Y también la capa tf.keras.layers.ReLU() tiene el mismo parámetro pero llamado negative_slope y obviamente hace exactamente lo mismo. Por lo tanto es igual a Leaky ReLU
model.add(Dense(3, input_dim=1,activation=tf.keras.layers.ReLU(negative_slope=0.3))) model.add(Dense(3, input_dim=1,activation=tf.keras.layers.Lambda(lambda x: tf.keras.activations.relu(x,alpha=0.3))))
Con el siguiente código podemos ver el resultado:
class_relu=tf.keras.layers.ReLU(negative_slope=0.3) class_leaky_relu=tf.keras.layers.LeakyReLU() x=np.linspace(-5,5,500) y_class_relu=class_relu(x) y_relu=tf.keras.activations.relu(x, alpha=0.3).numpy() y_class_leaky_relu=class_leaky_relu(x) np.set_printoptions(threshold=np.inf) np.set_printoptions(suppress=True) np.column_stack((y_relu,y_class_leaky_relu,y_class_relu,y_relu-y_class_leaky_relu,y_class_relu-y_class_leaky_relu))
Además en el código cuente de TensorFlow podemos ver como realmente son iguales:
PReLU
Existe otra capa de activación llamada PReLU que es similar a Leaky ReLU pero el valor de $\alpha$ se calcula automáticamente durante el entrenamiento, es decir que es como un parámetro mas de la red.
Mas información:
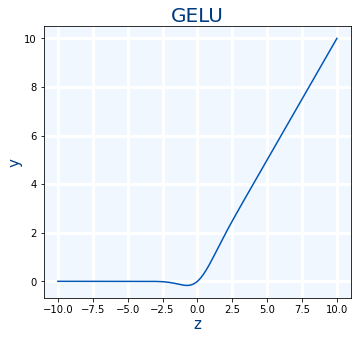
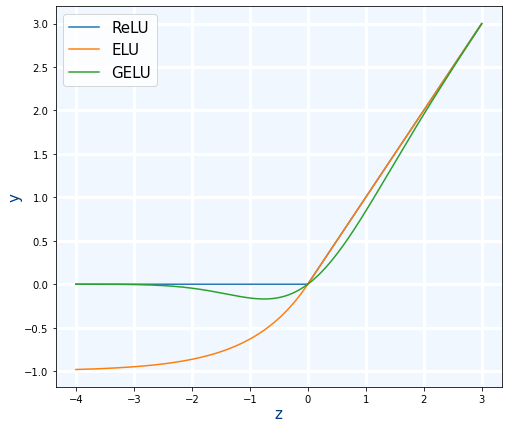
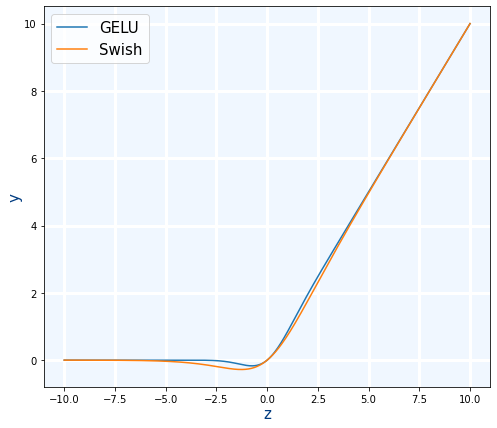
GELU
GELU es de la últimas funciones de activación "famosas" que han aparecido. GELU: Se usa con Transformers. La usa Google con BERT y OpenAI en GPT-2 y GPT-3.1)
$$ GELU(x)=0.5x(1+ \frac {2}{ \sqrt {\pi} } \int_{0}^{ \frac {x}{ \sqrt {2}}} e ^ {-t^{2}}dt) $$
- Uso en Keras
model.add(Dense(3, input_dim=1,activation=tf.keras.activations.gelu)) model.add(Dense(3, input_dim=1,activation="gelu"))
Mas información:
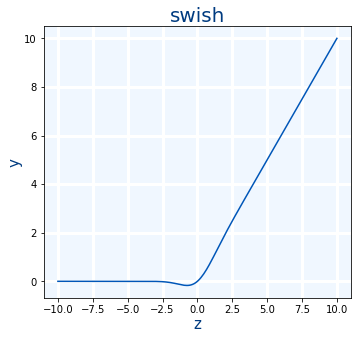
Swish
Se usa cuando ReLU pero es un poco más lenta pero es mejor.
$$swish(x)=x \cdot sigmoid(x)=x \cdot \frac{1}{1+e^{-x}}=\frac{x}{1+e^{-x}}$$
- Uso en Keras
model.add(Dense(3, activation=tf.keras.activations.swish)) model.add(Dense(3, activation="swish"))
- Swish: A Self-Gated Activation Function: Paper original de Swish
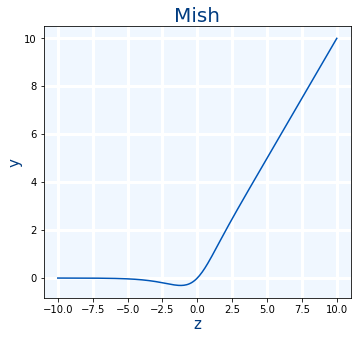
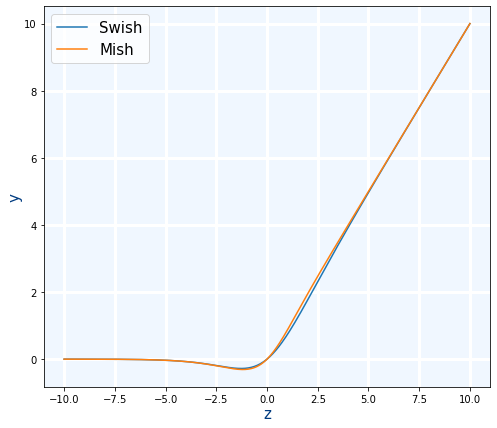
Mish
Se usa cuando ReLU pero aunque es un poco más lenta es mejor. Es muy similar a Swish
$$ mish(x)=x \cdot tanh(softplus(x)) $$
- Uso en Keras
model.add(Dense(3, activation=tf.keras.activations.swish)) model.add(Dense(3, activation="mish"))
- [https://www.tensorflow.org/api_docs/python/tf/keras/activations/mish|tf.keras.activations.mish(x)]]
- Mish: A Self Regularized Non-Monotonic Activation Function: Paper original de Mish
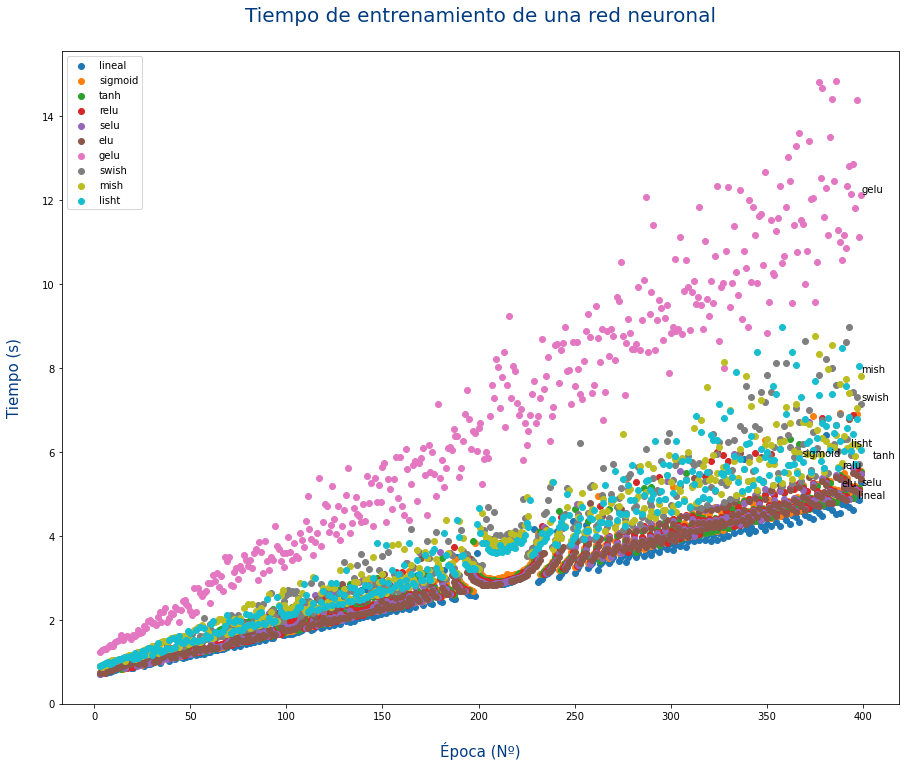
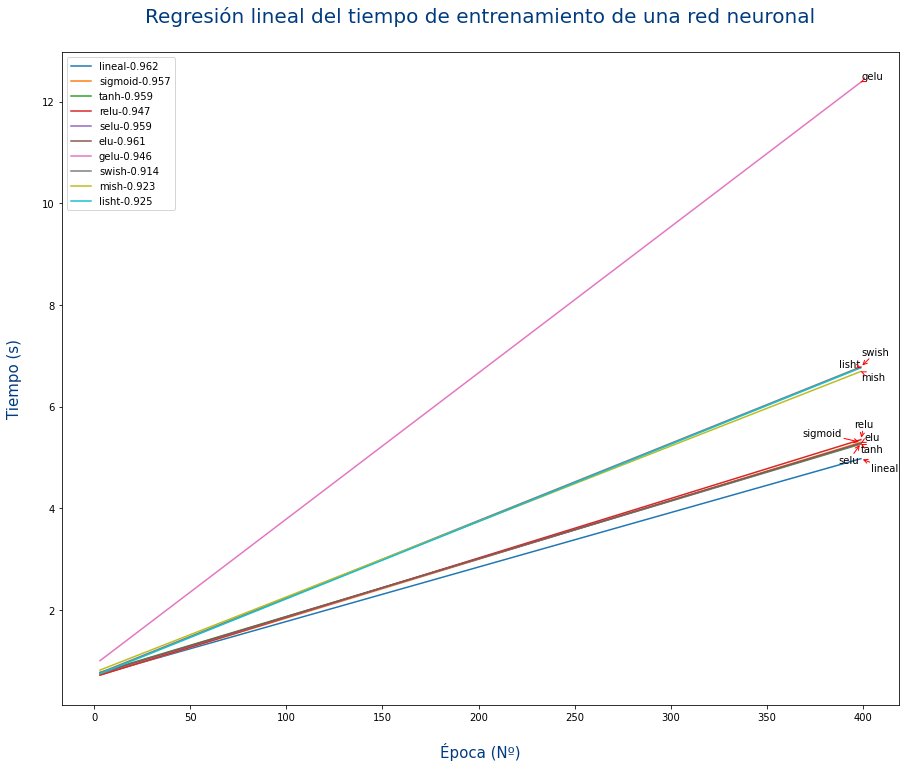
Tiempo de cálculo
Para cada problema puede que una función sea mejor que otra, es decir que cosiga entrenar en un menor número de épocas. Aun así a veces no puede preocupar el tiempo de CPU/GPU que usa cada función de activación.
En la siguiente gráfica se puede ver el tiempo de entrenamiento de una red neuronal con 14 capas y 1521 neuronas usando cada una de las funciones de activación.