Tabla de Contenidos
9.b Apendices
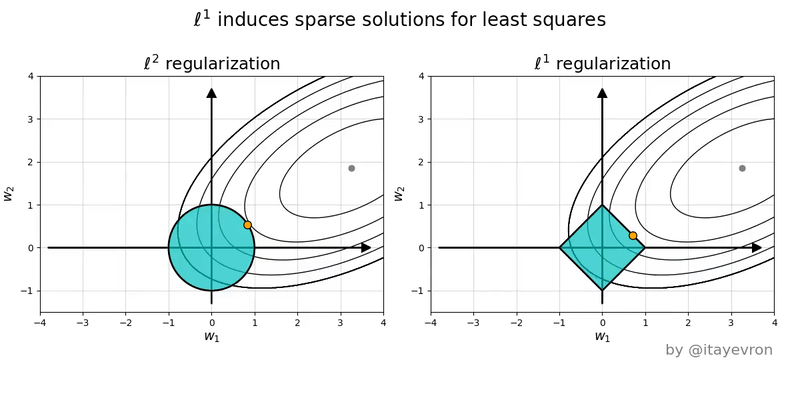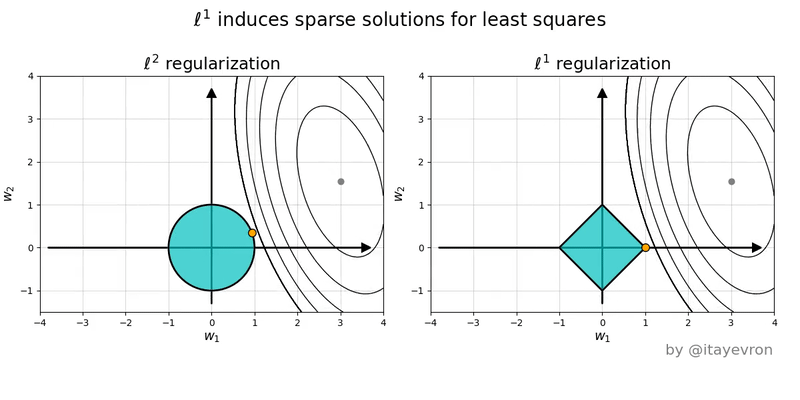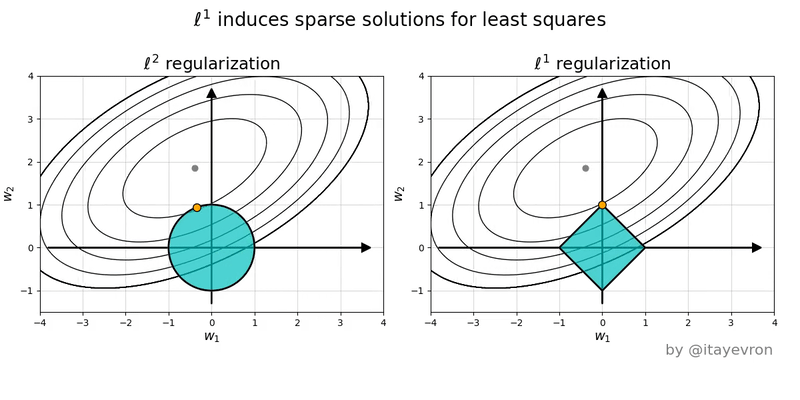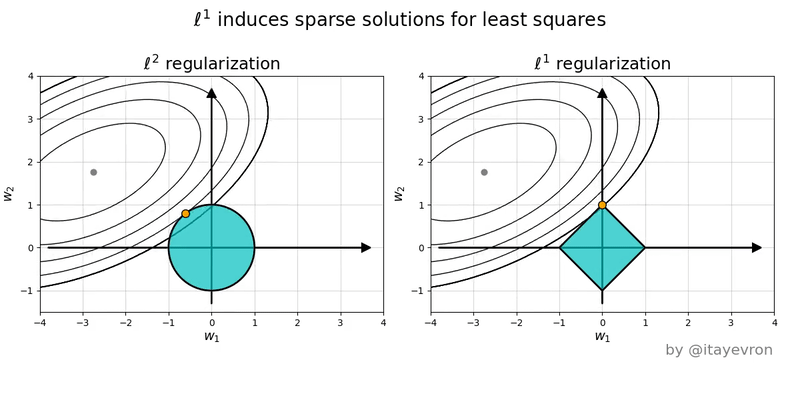
Regularización
Vamos a suponer la siguiente función de pérdida:
$$ Error=\frac 1 n \displaystyle\sum_{i=1}^{n} {(y_i-y'_i)^2 } $$
- $y$: Valor real
- $y'$: Valor predicho.
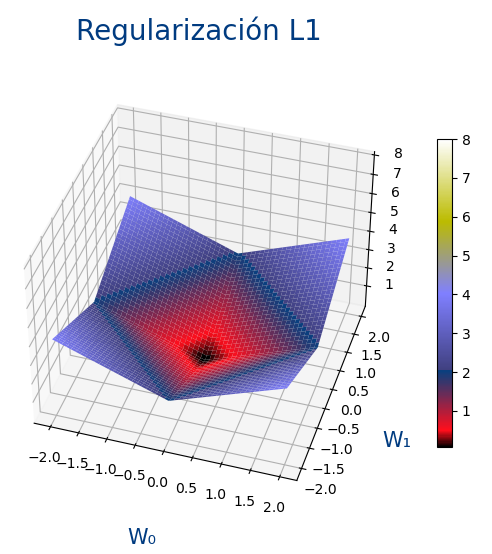
L1 (Lasso)
Hace que los pesos tiendan a ser cero
$$ Error=\frac 1 n \displaystyle\sum_{i=1}^{n} {(y_i-y'_i)^2 } + \alpha \frac 1 m \displaystyle\sum_{j=1}^{m} {|w_j|^1} $$
- α: Es cuanto queremos que regularicemos. Si vale 0, no se regulariza nada. Si vale 1 se regulariza muchísimo.
El uso del valor absoluto hace que cuanto mas pequeño sea el valor de w, menos sea el error.
Sirve para:
- Eliminar variables de entrada que no sirven.
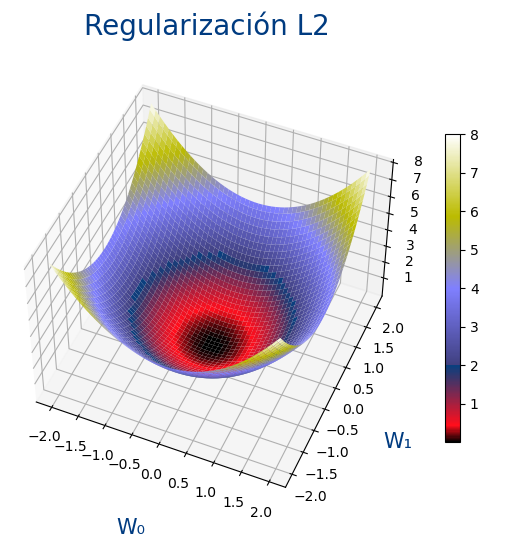
L2 (Ridge)
Hace que los pesos tiendan a tener un valor bajo pero no es necesario que sena tan bajos como con L1
$$ Error=\frac 1 n \displaystyle\sum_{i=1}^{n} {(y_i-y'_i)^2 } + \alpha \frac 1 {2m} \displaystyle\sum_{j=1}^{m} {|w_j|^2} $$
- α: Es cuanto queremos que regularicemos. Si vale 0, no se regulariza nada. Si vale 1 se regulariza muchísimo.
El uso de elevar al cuadrado hace que para valores entre -1 y 1, se hagan aun mas pequeños los w por lo que no es necesario que sena tan cercanos a cero.
Sirve para:
- Eliminar variables que están correlacionadas.
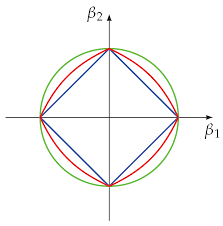
L1 y L2 (ElasticNet)
Es la unión de L1 y L2.
Parece un nuevo hiperparámetro r que indica si queremos que se de mas importancia a L1 o a L2.
- Si r vale 1, solo se hace regularización L1
- Si r vale 0, solo se hace regularización L2
- Si r vale 0,5, se le da la misma importancia a regularizar con L1 que con L2.
$$ Error=\frac 1 n \displaystyle\sum_{i=1}^{n} {(y_i-y'_i)^2 } + r \cdot \alpha \frac 1 m \displaystyle\sum_{j=1}^{m} {|w_j|^1} + (1-r) \cdot \alpha \frac 1 {2m} \displaystyle\sum_{j=1}^{m} {|w_j|^2} $$
- Azul: L1 (Lasso)
- Verde: L2 (Ridge)
- Rojo: L1 y L2 (ElasticNet)