−Tabla de Contenidos
9 Optimización de redes neuronales
Sobreajuste
El sobreajuste (en inglés Overfitting) es cuando nuestro modelo, en vez de aprender lo que hace es memorizar los resultados. Tambien existe el concepto de subajuste (en inglés underfitting) que es cuando el modelo no es lo suficientemente ponente para adecuarse a los datos. En redes neuronales suele darse menos el underfitting ya que las redes las podemos haces bastantes complejos y solemos pecar de modelos demasiado complejos.
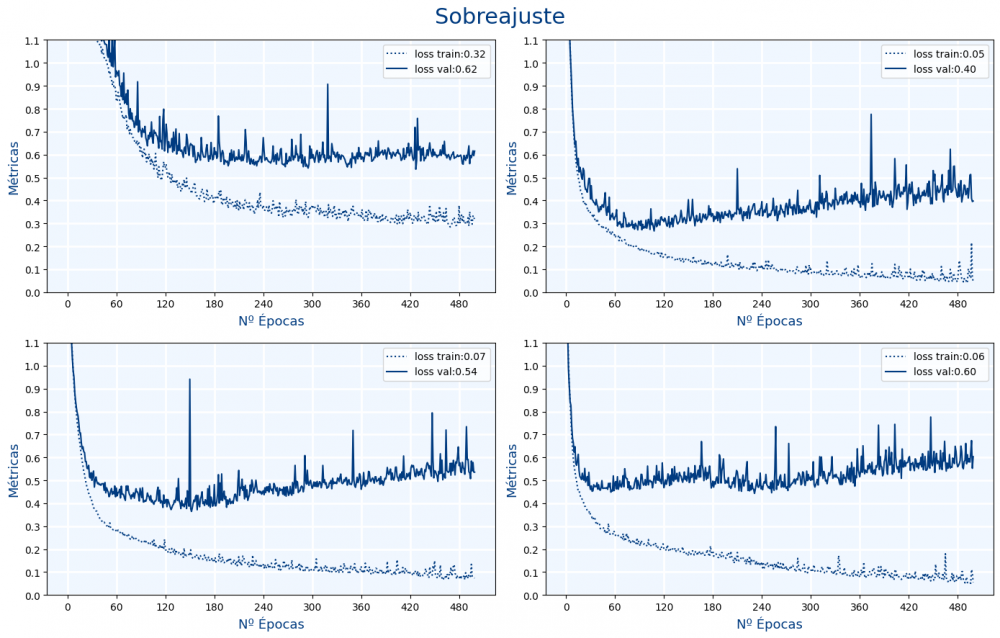
En las siguientes gráficas se observas distintos redes neuronales que tienen sobreajuste:
El sobreajuste se ve porque la red aprende cada vez más en entrenamiento pero aprende cada vez menos en validación. Es decir, disminuye la perdida en entrenamiento pero no disminuye en validación.
¿Como podemos evitar el sobre ajuste? Hay varias formas:
- Dropout
- Regularización
Regularización
Para hacer el modelo mas sencillo, la regularización intenta que los pesos sean mas pequeños. En una red neuronal tenemos una serie de pesos w y b. Si penalizamos la función de pérdida cuando los pesos son mas grandes, habremos "hecho" la regularización.
Se consigue que el tener el w o b muy bajo esa neurona "no exista" y por lo tanto simplifica el modelo. Un modelo más sencillo hace que haya menos sobre ajuste.
Existen 3 tipos de regularizadores (realmente existen más):
- L1: También llamada Lasso. Intenta hacer los pesos lo más pequeños posibles.
- L2: También llamada Ridge. Intenta eliminar correlaciones entre pesos.
- L1 y L2: También llamada ElasticNet. Es la unión de los 2 anteriores.
LossconL1=1nn∑i=1(yi−y′i)2+α1mm∑j=1|wj|1LossconL2=1nn∑i=1(yi−y′i)2+β12mm∑j=1|wj|2LosssconL1L2=1nn∑i=1(yi−y′i)2+α1mm∑j=1|wj|1+β12mm∑j=1|wj|2
Más información:
- Difference between L1 and L2 regularization, implementation and visualization in Tensorflow: Las imágenes en 3D de las 2 regularizaciones.
- How we express regularization in practice: Mas imágenes en 3D de L1 y L2
- Intuiciones sobre la regularización L1 y L2: Explica gracias a las derivadas porque L1 hace que el peso sea menor.
- l0-Norm, l1-Norm, l2-Norm, … , l-infinity Norm: Las normas (de matemáticas) que se usan en L1 y L2.
- De la regresión lineal a la regresión de crestas, el lazo y la red elástica: Están las gráficas de L1, L2 pero también L1+L2
Regularización en Keras
Los regularizadores se pueden aplicar tanto a los w como a los b:
kernel_regularizer: Para aplicarse a loswbias_regularizer: Para aplicarse a losb
w es decir usar kernel_regularizer.
Ejemplos de uso en Keras de L1:
1 2 3 4 5 |
from tensorflow.keras import regularizerskernel_regularizer=regularizers.L1(l1=0.01)kernel_regularizer="l1"model.add(Dense(neuronas_capa, activation=activation,kernel_regularizer=kernel_regularizer)) |
Ejemplos de uso en Keras de L2:
1 2 3 4 5 |
from tensorflow.keras import regularizerskernel_regularizer=regularizers.L2(l2=0.01)kernel_regularizer="l2"model.add(Dense(neuronas_capa, activation=activation,kernel_regularizer=kernel_regularizer)) |
Ejemplos de uso en Keras de L1L2:
1 2 3 4 5 |
from tensorflow.keras import regularizerskernel_regularizer=regularizers.L1L2(l1=0.01, l2=0.01)kernel_regularizer="l1_l2"model.add(Dense(neuronas_capa, activation=activation,kernel_regularizer=kernel_regularizer)) |
Los valores de l1, l2 que se pasa a los regularizadores es la tasa de regularización o cantidad de regularización y es cuanto queremos que regularicemos. Si vale 0, no se regulariza nada. Si vale 1 se regulariza muchísimo.
Analizando la regularización
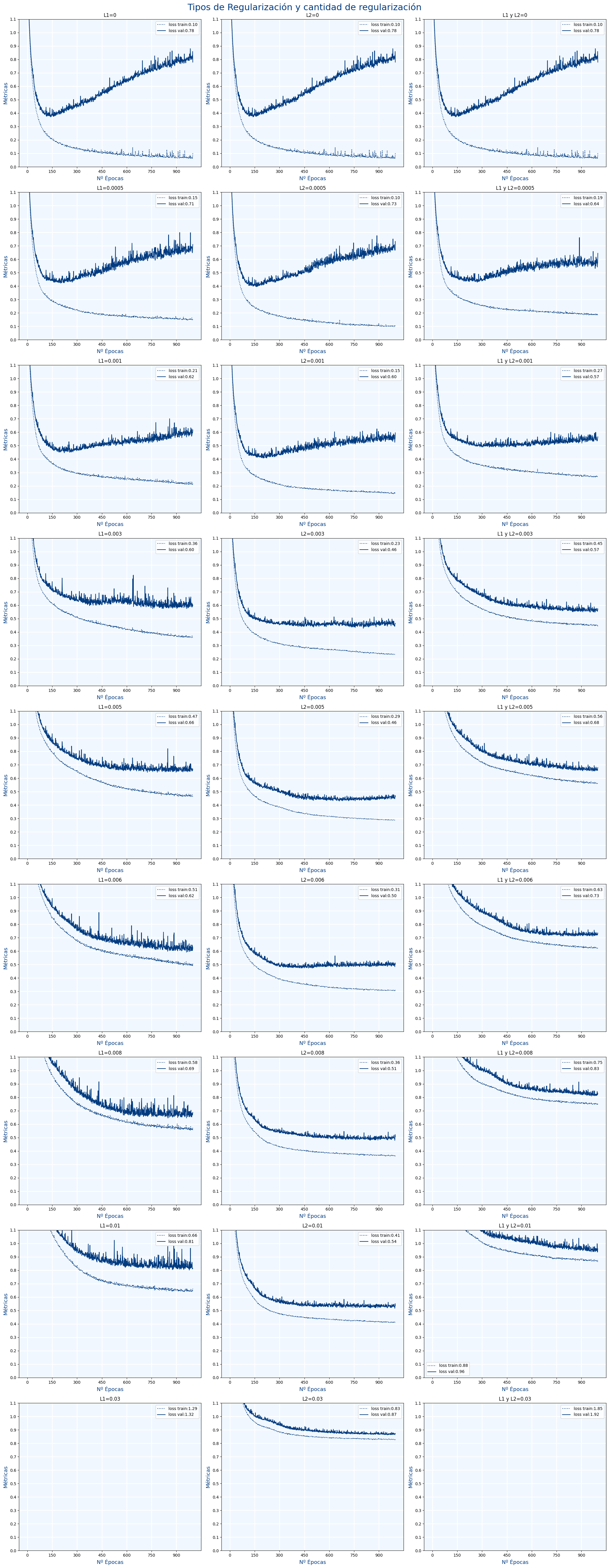
Vamos a ver como funcionan los distintos regularizadores y con distintos valores:
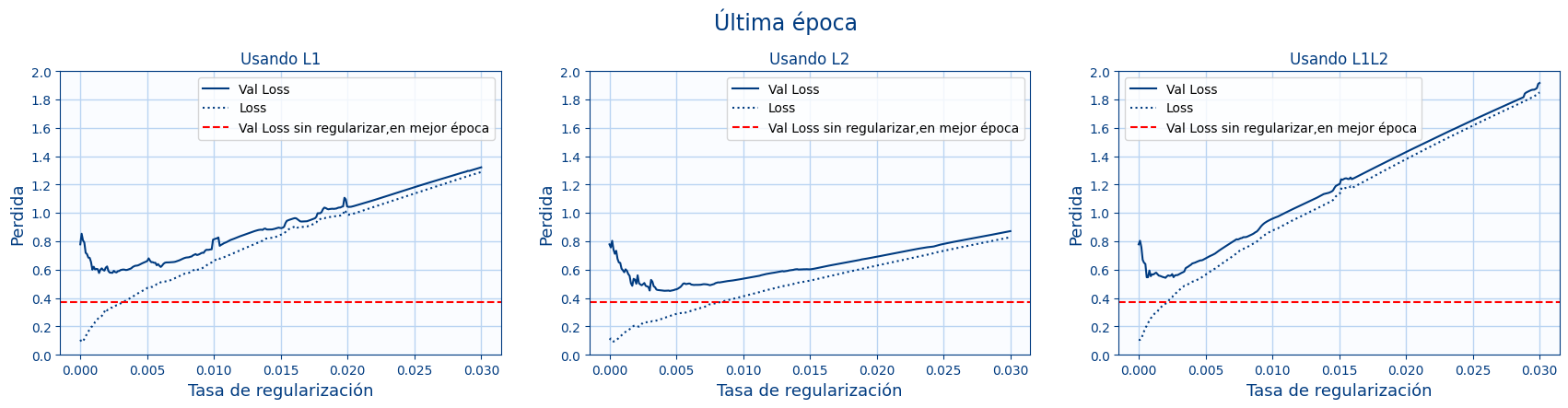
- En la siguiente gráfica vamos a mostrar el valor de la pérdida en la última época en función del nivel de regularización:
La línea roja indica para la red sin regularizar el mejor valor de todas las épocas. Es decir es el valor cuando aun no hay sobre ajuste y por lo tanto pocas épocas. La gráfica muestra la pérdida de la última época para cada tasa de regularización. Se puede apreciar que con un poco de regularización se mejora la red , pero nunca llega a estar por debajo de la línea roja. Es decir se ve que entrenar más y aplicar regularización no supone ninguna mejora.
- En la siguiente gráfica vamos a mostrar el valor de la pérdida en la mejor época en función del nivel de regularización:
Esta gráfica es similar a la anterior pero ahora se muestra la mejor pérdida (para cualquier época) en vez de la perdida de la última época.En ese caso la línea roja coincide con el primer punto de "Val loss" ya que es cuando no hay regularización. En ese caso también se ve que entrenar más y aplicar regularización no supone ninguna mejora en ninguna de las épocas.
- Entrenar pocas épocas antes de que haya sobreajuste y no necesitar ninguna regularización.
- Entrenar durante muchas épocas aunque haya sobreajuste y aplicar regularización
La opción a elegir dependerá del problema y hay que probar ambas opciones para saber cual es la mejor opción.
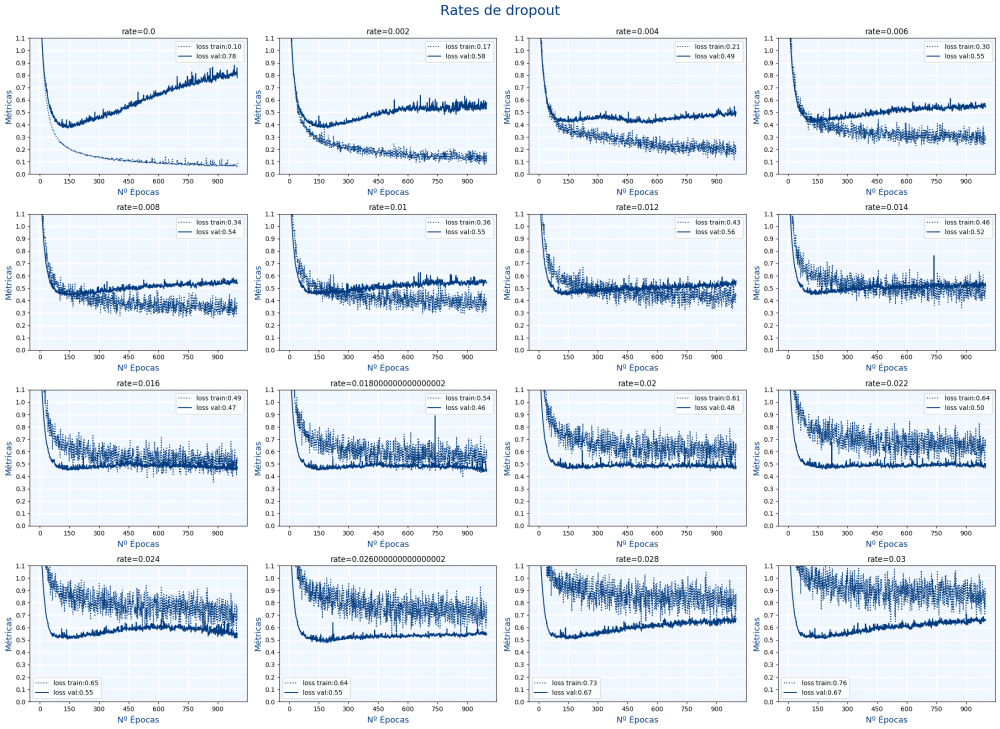
Dropout
El Dropout consiste en hacer que ciertas neuronas se vayan desactivando cada vez en el entrenamiento.
Se hace añadiendo capas de Dropout con una tasa (rate) de cuantas neuronas se desactivan. Un valor de 0 es como si no hubiera dropout y un valor cercano a 1 es como si se desactivaran la mayoría de neuronas. (No se permite el valor de 1)
Uso de uso en Keras de Dropout:
1 2 3 4 5 |
from tensorflow.keras.layers import Dropoutdropout_rate=0.02model.add(Dense(neuronas_capa, activation=activation))model.add(Dropout(rate=dropout_rate)) |
Optimización
Junto con las técnicas anteriores , existen otras para mejorar una red neuronal:
- Normalization
- Tamaño de Batch
- Batch Normalization
- Parada anticipada
Normalization
La normalización consiste es que los datos de entrada estén centrado en 0 y una desviación "pequeña". Esto se hace porque la red va a entrenarse mejor si los datos son "pequeños" y todos en la misma escala ya que así funciona mejor el algoritmo del descenso de gradiente.
Para normalizar los datos se usa la clase StandardScaler de sklearn.
1 2 3 4 5 |
from sklearn.preprocessing import StandardScalerstandard_scaler = StandardScaler()standard_scaler.fit(x)x_standard = standard_scaler.transform(x) |
Y sobre un ejemplo de datos sería lo siguiente:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def get_datos_bread_cancer(): datos=load_breast_cancer() x=datos.data y=datos.target standard_scaler = StandardScaler() standard_scaler.fit(x) x = standard_scaler.transform(x) x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=42,stratify=y) state={ "mean":standard_scaler.mean_, "var":standard_scaler.var_, "scale":standard_scaler.scale_ } return x_train, x_test, y_train, y_test, statex_train, x_test, y_train, y_test,state=get_datos_bread_cancer() |
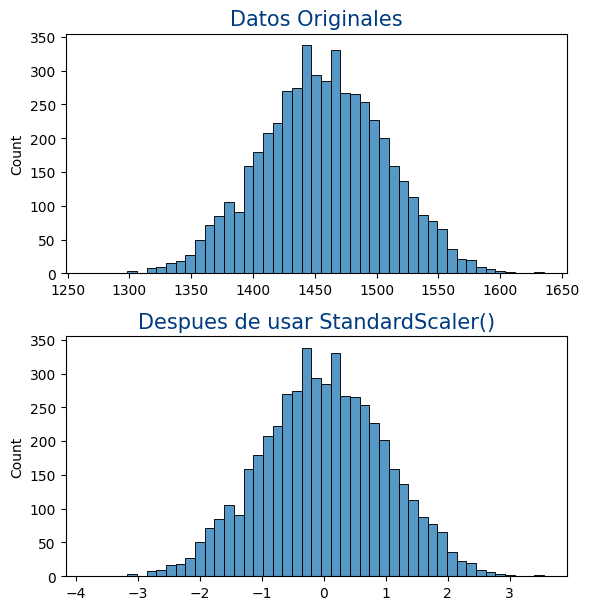
Veamos un ejemplo de que es lo que realmente hace.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
from sklearn.preprocessing import StandardScalerdatos=np.random.normal(1000,50,5000).reshape(-1,1)figure=plt.figure(figsize = (6, 9))axes = figure.add_subplot(3,1,1)sns.histplot(x=datos.reshape(-1),ax=axes)standard_scaler = StandardScaler()standard_scaler.fit(datos)datos_standarized = standard_scaler.transform(datos)axes = figure.add_subplot(3,1,2)sns.histplot(x=datos_standarized.reshape(-1),ax=axes)figure.suptitle("StandardScaler", fontsize=22, color='#003B80') |
Un problema que hay al usar la clase StandardScaler es que en producción hay que usar la misma transformación para predecir los datos. Por ello es necesario guardar los datos de la clase para volver a ponerlos.
La forma de hacerlo es la siguiente:
1 2 3 4 5 6 7 8 9 10 11 12 13 |
state={ "mean":standard_scaler.mean_, "var":standard_scaler.var_, "scale":standard_scaler.scale_}new_standard_scaler = StandardScaler()new_standard_scaler.fit([[0]])new_standard_scaler.mean_=state["mean"]new_standard_scaler.var_=state["var"]new_standard_scaler.scale_=state["scale"]new_datos_standarized = new_standard_scaler.transform(datos)print("Iguales=",np.array_equal(datos_standarized,new_datos_standarized)) |
Iguales= True
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
class DataScaler: def __init__(self,x,y,scaler=StandardScaler): self.x=x self.y=y self.scaler=scaler if (np.ndim(x)==1): self.x_ndim=1 else: self.x_ndim=x.shape[1] if (np.ndim(y)==1): self.y_ndim=1 else: self.y_ndim=y.shape[1] def get_datos_escalados_entrenamiento(self): self.x_scaler = self.scaler() self.y_scaler = self.scaler() x_scaled = self.x_scaler.fit_transform(self.x.reshape(-1,self.x_ndim)) y_scaled=self.y_scaler.fit_transform(self.y.reshape(-1,self.y_ndim)) return x_scaled,y_scaled def get_datos_reales(self): return self.x,self.y def predict(self,model,x_pred): y_pred=self.y_scaler.inverse_transform(model.predict(self.x_scaler.transform(x_pred.reshape(-1,self.x_ndim)))) return y_pred |
Batch Normalization
Hace que las salida sigan con valores alrededor de media 0 y desviación 1.
1 2 |
model.add(Dense(neuronas_capa, activation=activation))model.add(BatchNormalization()) |
Tamaño del Batch
1 |
history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=40,verbose=False,batch_size=20) |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def fit(x, y_true,epochs,batch_size,learning_rate,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5): #Divide los datos en batchs x_batchs=np.split(x, np.arange(batch_size,len(x),batch_size)) y_true_batchs=np.split(y_true, np.arange(batch_size,len(y_true),batch_size)) num_batchs=len(x_batchs) for epoch in range(epochs): for i in range(num_batchs): x_batch=x_batchs[i] y_true_batch=y_true_batchs[i] w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5=descenso_gradiente(x_batch,y_true_batch,learning_rate,w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5) return w_2,w_3,w_4,w_52,w_53,w_54,b_2,b_3,b_4,b_5 |
Callbacks
Guardar mejor modelo
Al entrenar no siempre la última época es el mejor modelo, por ello hay un callback de keras que nos guarda el mejor modelo. Se llama ModelCheckpoint.
La clase contiene entre otros los siguientes parámetros:
filepath: Nombre del fichero donde se guarda el modelomonitor: La métrica a monitorizar. Por defecto monitorizaval_loss.mode: Indica el tipo de métrica que es. Es decir si la métrica es mejor cuanto mayor valor tiene (max) o la métrica es mejor cuanto menor valor tiene (min). Por defecto es valor esautoy keras sabrá el tipo de la métrica por el nombre que tiene.save_best_only=True: Guardar solo el mejor modelo porque sino guara todos y no nos suele interesar.
1 2 3 4 5 6 7 8 9 10 11 |
from tensorflow.keras.callbacks import ModelCheckpointcheckpoint_callback = ModelCheckpoint( 'best_model.h5', monitor='val_loss', save_best_only=True, mode='min')history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=40,verbose=False,callbacks=[checkpoint_callback()]) |
Parada anticipada
La parada anticipada resuelve el problema de cuántas épocas debemos entregar nuestro modelo. Lo que hace es detener el entrenamiento si la métrica no mejora. Para ello se usa la clase de callback de keras llamado EarlyStopping().
La clase contiene entre otros los siguientes parámetros:
monitor: La métrica a monitorizar. Por defecto monitorizaval_loss.min_delta: El mínimo valor que consideramos como una mejora. Si mejora menos que este valor lo consideraremos como que no ha mejorado. Por defecto si valor es 0.patience: Cuántas épocas puede estar sin mejorar antes de que paremos el entrenamiento. Por defecto vale 0.mode: Indica el tipo de métrica que es. Es decir si la métrica es mejor cuanto mayor valor tiene (max) o la métrica es mejor cuanto menor valor tiene (min). Por defecto es valor esautoy keras sabrá el tipo de la métrica por el nombre que tiene.restore_best_weights: Si es True, restaurará los pesos del modelo a la mejor versión del entrenamiento, es decir, la versión que tuvo el mejor valor en la métrica monitorizada.
1 2 3 4 5 6 7 8 9 10 11 12 13 |
from tensorflow.keras.callbacks import EarlyStoppingearlystopping_callback = EarlyStopping( monitor='val_loss', # Métrica a monitorear min_delta=0.001, # Mejora mínima a considerar significativa patience=10, # Esperar 10 épocas sin mejora antes de detenerse mode='min', # Monitorizar si la pérdida disminuye restore_best_weights=True # Restaurar los mejores pesos)history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=40,verbose=False,callbacks=[earlystopping_callback()]) |
ModelCheckpoint si ya EarlyStopping nos permitirá obtener el mejor modelo con restore_best_weights=True. Si ,porque si falla el entrenamiento , con ModelCheckpoint se va guardando a disco y así nunca lo perderemos.
Más información:
Ejercicios
Ejercicio 1.A
Crea una red neuronal para predecir si una persona va a tener una enfermedad cardíaca. Para ello se han usado los datos de heart-disease-health-indicators-dataset.
Las columnas del dataset son las siguientes:
- HeartDiseaseorAttack: Indica si el individuo ha experimentado una enfermedad cardíaca o un ataque al corazón. Es lo que hay que predecir.
- HighBP: Indica si el individuo tiene presión arterial alta.
- HighChol: Indica si el individuo tiene niveles altos de colesterol.
- CholCheck: Indica si el individuo ha realizado chequeos de colesterol.
- BMI: Índice de Masa Corporal del individuo.
- Smoker: Indica si el individuo fuma.
- Stroke: Indica si el individuo ha experimentado un derrame cerebral.
- Diabetes: Indica si el individuo tiene diabetes.
- PhysActivity: Nivel de actividad física del individuo.
- Fruits: Consumo de frutas por parte del individuo.
- Veggies: Consumo de vegetales por parte del individuo.
- HvyAlcoholConsump: Indica si el individuo consume mucho alcohol
- AnyHealthcare: Indica si el individuo tiene acceso a algún tipo de atención médica.
- NoDocbcCost: Indica si el individuo tiene costos médicos sin documentar.
- GenHlth: Estado general de salud del individuo.
- MentHlth: Estado de salud mental del individuo.
- PhysHlth: Estado de salud física del individuo.
- DiffWalk: Dificultad para caminar del individuo.
- Sex: Género del individuo.
- Age: Edad del individuo.
- Education: Nivel educativo del individuo.
- Income: Ingreso económico del individuo.
Los datos son los siguientes: heart_disease_health_indicators_brfss2015.csv.zip
Ejercicio 1.B
Mejora la red normalizando los datos . Usa StandardScaler.
¿Ha mejorado la red?
Ejercicio 1.C
Modifica la red de forma que haya muchas neuronas y que haya sobreajuste.
Debes mostrar una gráfica en la que se vea el loss en entrenamiento y validación.
Ahora vamos a comprobar si es mejor regularizar (L1, L2 y L1L2) o simplemente no sobreentrenar para ello crea una gráficas similares a éstas:
Ejercicio 1.D
Repite ahora las gráficas pero en vez de regularizar, usa Dropout
Ejercicio 1.E
Usa ahora EarlyStopping y ModelCheckpoint para obtener el modelo evitando que se entrene durante tantas épocas y que se guarde a disco automáticamente.