−Tabla de Contenidos
6. Redes neuronales
Al principio del curso vimos un esbozo de una red neuronal, en este tema vamos a profundizar en las redes neuronales.
Como vimos una red neuronal no es más que una función matemática de la forma:
→y=f(→x)
- →x es el vector de entrada a la red neuronal
- →y es el vector de salida de la red neuronal.
En el caso de las flores era:
tipoflor=f(largosépalo,largopétalo)
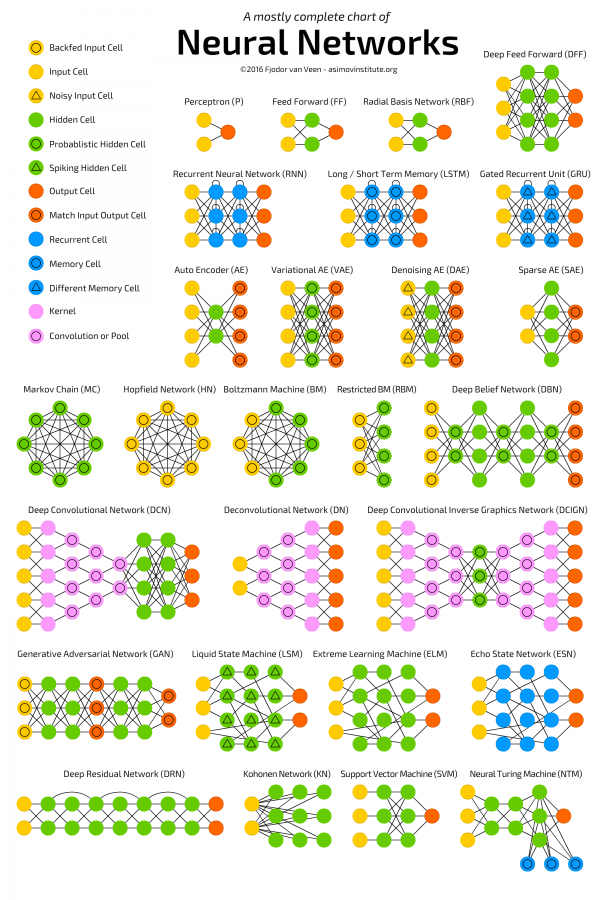
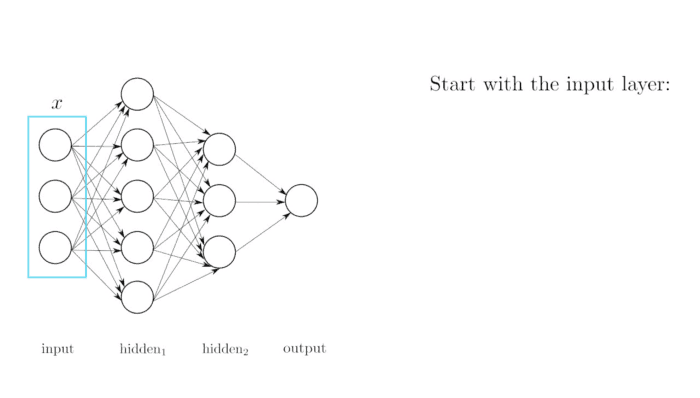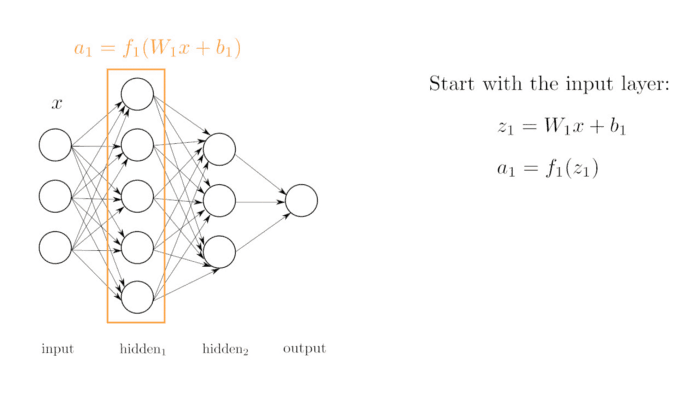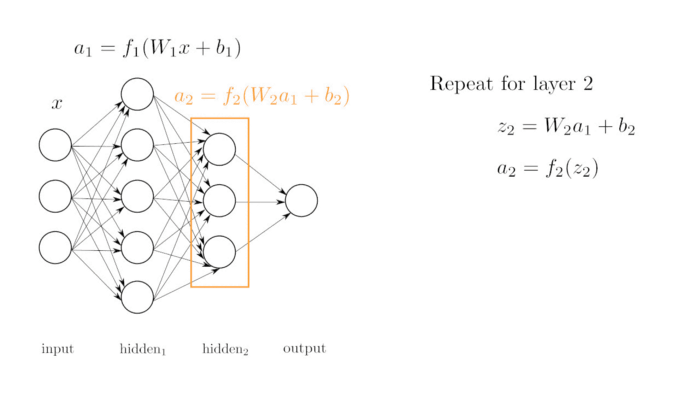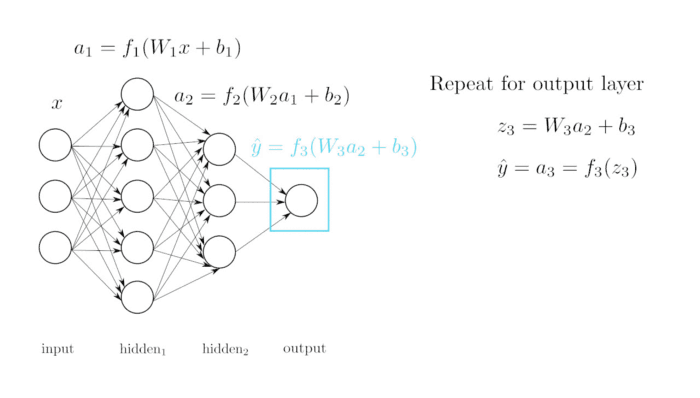
Y la red neuronal que vimos de ejemplo era:
Esta red neuronal, consta de una serie de neuronas que se pasan valores de unas a otras. Son cada uno de los círculos. Las neuronas se organiza en capas:
- Capa de entrada (Círculos amarillos): Es una única capa por donde entran los datos de entrada. Es decir los valores del largo del sépalo y el largo del pétalo. Por lo tanto en este caso debe haber 2 neuronas , una por cada valor de entrada.
- Capas ocultas (Círculos verdes): Son varias capas, las cuales calculan de que tipo es cada flor. La primera capa oculta consta de 6 neuronas. La segunda capa oculta consta de 12 neuronas . La última capa oculta consta de 6 neuronas.
- Capa de salida (Círculos rojos): Es una única capa que es la que genera el resultado de la red neuronal. Como la red genera un único número la capa tiene solo 1 neurona.
Mas información:
Neurona
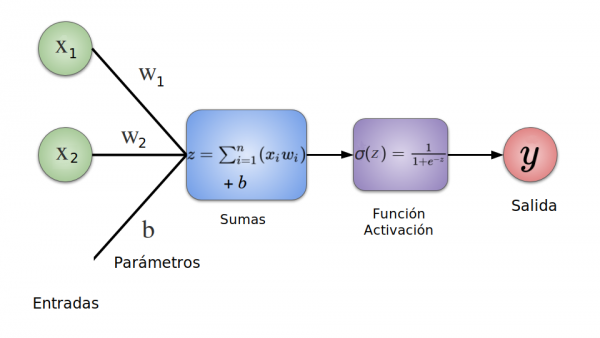
Pasemos a ver que es una neurona. La neurona no es mas que otra función matemáticas que por ahora es solo un polinomio de primer grado.
En su forma mas sencilla una neurona es únicamente lo siguiente:
y=wx+b
Es decir que a cada neurona le entra el valor de entrada llamado x, y calcula el valor de salida llamado y y para ello usa la fórmula wx+b. Y esa fórmula es la ecuación de una recta.
Si la entrada en vez de ser un único valor de x fueran varios valores, la fórmula quedaría así:
y=w1x1+w2x2+w3x3...+wnxn+b
que puesto en forma de vectores sería:
y=→w⊺⋅→x+b
Por ejemplo si hubiera 3 valores de entrada llamados x1, x2 y x3. La formula sería:
y=w1x1+w2x2+w3x3+b
El siguiente esquema resume como es una neurona:
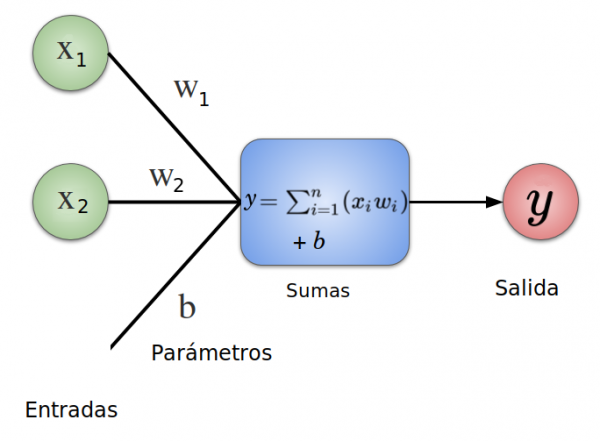
Lo siguiente a ver es ¿Que son los w y b que hay en la fórmula? Es lo que se llama pesos y sesgos que vienen del ingles weight y bias. Esos 2 valores es lo que se llaman parámetros de una red neuronal. Esos valores los desconocemos y al crear la red neuronal se eligen aleatoriamente pero al entrenar la red reuronal con el método fit, lo que hace la red neuronal es justamente calcular los parámetros pesos w y sesgos b más adecuados
w y b
Red Neuronal
Pasemos ahora a explicar que es una red neuronal. No es mas que muchas neuronas conectadas entre ellas.
En la siguiente imagen se pueden ver diversos tipos de redes neuronales
Mas información:
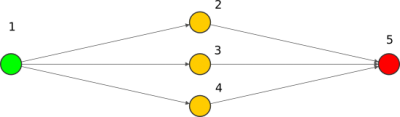
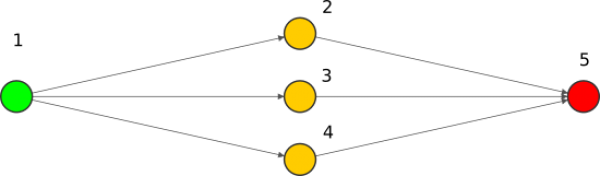
Pasemos ahora a ver un ejemplo simple con 5 neuronas.
Veamos esta red y como son cada una de las neuronas.
| Nº Neurona | Formula | Explicación |
|---|---|---|
| 1 | y1=x | Como es una neurona de entrada , realmente no hace nada. Su salida realmente es la entrada ya que solo captura los datos de entrada. |
| 2 | y2=w2y1+b2 | Esta neurona obtiene su entrada de la salida de la neurona anterior que es y1 |
| 3 | y3=w3y1+b3 | Esta neurona obtiene su entrada de la salida de la neurona anterior que es y1 |
| 4 | y4=w4y1+b4 | Esta neurona obtiene su entrada de la salida de la neurona anterior que es y1 |
| 5 | y5=w5,2y2+w5,3y3+w5,4y4+b5 | Esta neurona obtiene su entrada de las salidas de las 3 neuronas anteriores que son y2 , y3 e y4 |
Pero sabiendo que y1=x, podemos substituirlo en las neuronas 2, 3 y 4
| Nº Neurona | Formula |
|---|---|
| 2 | y2=w2y1⏞x+b2 |
| 3 | y3=w3y1⏞x+b3 |
| 4 | y4=w4y1⏞x+b4 |
y finalmente como ya sabemos lo que vale y2 , y3 e y4 podemos substituirlo en la neurona 5.
| Nº Neurona | Formula |
|---|---|
| 5 | y5=w5,2y2⏞(w2x+b2)+w5,3y3⏞(w3x+b3)+w5,4y4⏞(w4x+b4)+b5 |
Ahora si decíamos que una red neuronal es solo una función matemática que calcula una y en función de una x ya tenemos la fórmula:
y=f(x)=w5,2(w2x+b2)+w5,3(w3x+b3)+w5,4(w4x+b4)+b5
Y el cálculo de todos esos parámetros ( w2,w3,w4,w5,2,w5,3,w5,4,b4,b2,b3,b5) es lo que se hace al entrenar la red con todos los datos de entrada de todas las posibles x y todos los resultados de y.
¿Como sería esa red programada en Keras?
1 2 3 4 |
model=Sequential()model.add(Dense(3, input_dim=1))model.add(Dense(1))model.compile() |
Mas información:
Tamaño red neuronal
Pasemos ahora a ver el tamaño una red neuronal. Para ver el tamaño podríamos medirlo por el número de neuronas pero hemos visto que hay neuronas mas simples y mas complejas
- Neurona Ejemplo A: y=w1x1+b
- Neurona Ejemplo B: y=w1x1+w2x2+w3x3+w4x4+w5x5+b
La neurona A es mas sencilla que la neurona B. Por ello para determinar el tamaño de la red lo que se cuenta es la suma de los parámetros de todas sus neuronas.
- Neurona A: Tiene 2 parámetros (w1,b)
- Neurona B: Tiene 6 parámetros (w1,w2,w3,w4,w5,b)
Calculemos ahora cuantos parámetros tiene la red que hemos visto antes.
- La capa de entrada no contiene parámetros.
- La capa oculta (Color amarilla) contiene 6 parámetros ( w2,w3,w4,b2,b3,b4 )
- La capa de salida (Colo roja) contiene 4 parámetros ( w5,2,w5,3,w5,4,b5 )
Es decir que en total son 10 parámetros.
Con Keras podemos saber el Nº de parámetros de cada capa y los totales con el método summary()
1 |
model.summary() |
Model: "sequential" _________________________________________________________________ Layer (type) Output Shape Param # ================================================================= dense (Dense) (None, 3) 6 _________________________________________________________________ dense_1 (Dense) (None, 1) 4 ================================================================= Total params: 10 Trainable params: 10 Non-trainable params: 0 _________________________________________________________________
El método summary() demás de indicarnos en Nº de parámetros de cada capa , también nos indica el Nº de neuronas de cada capa. Fijaros que no aparece la primera capa ya que nunca tiene ningún parámetro para entrenar.
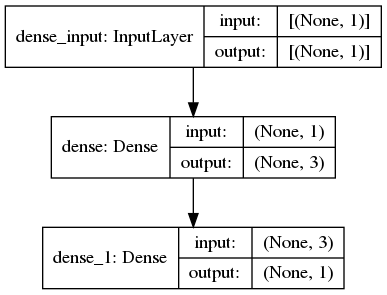
También podemos ver la estructura de la red neuronal con el método plot_model()
1 2 3 |
from tensorflow.keras.utils import plot_modelplot_model(model, show_shapes=True) |
Podemos ver para cada capa el Nº de entradas y salidas. El Nº de salidas determinará el Nº de neuronas que tendrá esa capa.
Mas información:
Parámetros en Keras
En Keras para ver los valores exactos de cada parámetro de la red neuronal se usa el método .get_weights. Este método retorna tanto los weight como los bias
Sigamos con el ejemplo pero vamos a explicar como Keras numera las neuronas. Lo que hace es organizar las neuronas en capas (layers)y numerar cada neurona con un número dentro de la capa.
La capa de entrada como no hace ningún cálculo es como si no existiera por eso la primera capa oculta es la capa "0" y la de salida al ser la siguiente es la capa "1". Luego dentro de cada capa, las neuronas se enumeran desde el "0" hasta el número de neuronas menos 1.
Para simplificar la obtención de los valores de los parámetros hemos creado dos funciones:
get_w: Obtiene el weight de una neurona. Los argumentos son:model: El modelo de red neuronal sobre el que se van a obtener los weightlayer: El Nº de la capa en la que se encuentra la neuronaneuron: El Nº de la neurona dentro de la capa. Se empieza por 0index: Dentro de la neurona puede haber varios weight, así que este argumento indica cual de todos ellos retornará.Empieza por 0.
get_b: Obtiene el bias de una neurona. Los argumentos son:model: El modelo de red neuronal sobre el que se van a obtener los biaslayer: El Nº de la capa en la que se encuentra la neuronaneuron: El Nº de la neurona dentro de la capa. Se empieza por 0
1 2 3 4 5 6 7 8 9 |
def get_w(model,layer,neuron,index): layer=model.layers[layer] return layer.get_weights()[0][index,neuron]def get_b(model,layer,neuron): layer=model.layers[layer] return layer.get_weights()[1][neuron] |
Usando las funciones que acabamos de crear vamos a obtener cada uno de los parámetros
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
#weights y bias cada neurona de la capa 0 w_2=get_w(model,0,0,0)b_2=get_b(model,0,0)w_3=get_w(model,0,1,0)b_3=get_b(model,0,1)w_4=get_w(model,0,2,0)b_4=get_b(model,0,2)#weights y bias de la única neurona de la capa 1w_52=get_w(model,1,0,0)w_53=get_w(model,1,0,1)w_54=get_w(model,1,0,2)b_5 =get_b(model,1,0) |
Inicialización de parámetros
Hemos indicado antes que cuando se define la red neuronal con compile, Keras genera valores aleatorios para los parámetros y luego con el método fit se entrena la red neuronal para averiguar los valores mas adecuados.
Cuando decimos que los parámetros de inicializan de forma aleatoria ¿que distribución siguen? ¿distribución Normal ,distribución Uniforme, etc? Pues bien , en ciertos casos es necesario definir exactamente cual es la forma de inicializar los parámetros.
En keras al crear una capa podemos indicar como se inicializan los pesos (weights) y como se inicializan los sesgos (bias), para ello están los siguientes parámetros:
kernel_initializer: Indica la forma en la que se inicializan los pesos (weights). Por defecto se usaglorot_uniformbias_initializer: Indica la forma en la que se inicializan los sesgos (bias). Por defecto se usazeros
1 2 3 4 |
model=Sequential()model.add(Dense(3, input_dim=1,kernel_initializer="glorot_uniform",bias_initializer="zeros"))model.add(Dense(1))model.compile() |
En el ejemplo los pesos (weights) se inicializan de la forma "Glorot Uniforme" y los sesgos (bias) mediante "ceros".
bias_initializer no se suele usar.
Los siguientes son los posibles inicializadores en Keras:
zeros: Se inicializa todo con 0.ones: Se inicializa todo con 1- Uniformes: Usan la distribución uniforme para generar los datos entre los dos valores [−limit,limit]
random_uniform: limit=0.05glorot_uniform: limit=√3fanin+fanout2=√6fanin+fanouthe_uniform: limit=√6faninlecun_uniform: limit=√3fanin
- Normal: Usan la distribución Normal para generar los datos. media=0 , lo que cambia es la desviación estándar
random_normal: desviaciónestándar=0.05glorot_normal: desviaciónestándar=√1fanin+fanout2=√2fanin+fanouthe_normal: desviaciónestándar=√2faninlecun_normal: desviaciónestándar=√1fanin
Siendo:
fanin=elnºdeentradasdelacapa
fanout=elnºdesalidasdelacapa
- El inicializador
glorottambién se puede llamar Xavier ya que el autor es Xavier Glorot. - El inicializador
hetambién se puede llamar Kaiming ya que el autor es Kaiming He. - El inicializador
lecuntambién se puede llamar Yann ya que el autor es Yann LeCun.
La pregunta ahora es ¿que inicializador usar? Por defecto Keras usa para los pesos (weights) el inicializador glorot_uniform y para los sesgos (bias) el inicializador zeros.
Los inicializadores de los pesos (weights) dependen de la función de activación y se recomiendan los siguientes:
| Inicializador | Función de Activación |
|---|---|
| Glorot Normal | Ninguna, sigmoide, tanh, softmax |
| He Uniform | ReLu y sus variantes |
| LeCum Normal | SELU |
| LeCum Uniform | GELU |
Mas información:
- Weight Initialization in Neural Net: Ejemplos en Keras.
Funciones de activación
Si sabes de matemáticas te puedes haber dado cuenta que falta algo en una neurona. Resulta que si cada neurona es un polinómio de primer grado ( y=wx+b ) la unión con otras neuronas acaba siendo también otro polinomio de primer grado, con lo que no serviría para nada hacer una red neuronal.
Recordemos la red neuronal
Cuya función era:
y=f(x)=w5,2(w2x+b2)+w5,3(w3x+b3)+w5,4(w4x+b4)+b5
Si agrupamos un poco los términos, se puede queda la expresión de la siguiente forma:
y=f(x)=(w5,2w2+w5,3w3+w5,4w4)x+(w5,2b2+w5,3b3+w5,4b4+b5)
Si creamos dos nuevas variable llamas W y B
W=w5,2w2+w5,3w3+w5,4w4B=w5,2b2+w5,3b3+w5,4b4+b5
Entonces
y=f(x)=Wx+B
¡¡¡¡¡¡¡Así que la red se podría haber simplificado a una única neurona de entrada y otra de salida!!!!
Para que realmente funcionen las redes neuronales hay que añadir "algo" que cree una "no linealidad". Ésto se consigue con la función de activación.
Para añadir la función de activación vamos a cambiar un poquito la nomenclatura que hemos usado hasta ahora. La salida de la función lineal a partir de ahora la vamos a llamar z en vez de y ya que la y sigue siendo la salida de la neurona pero después de aplicar la función de activación a z.
z=wx+b
y=σ(z)
Siendo σ (sigma ) el nombre que le vamos a dar a la función de activación.
Una función de activación sencilla es la llamada "función sigmoide" y es la siguiente fórmula :
σ(z)=11+e−z
Por lo que la neurona queda de la siguiente forma:
z=wx+by=σ(z)σ(z)=11+e−z}y=11+e−(wx+b)
Así que vamos a cambiar la fórmula de nuestra red neuronal incluyendo la función de activación sigmoide:
| Nº Neurona | Formula |
|---|---|
| 1 | y1=x |
| 2 | y2=σ(w2y1+b2)=11+e−(w2y1+b2) |
| 3 | y3=σ(w3y1+b3)=11+e−(w3y1+b3) |
| 4 | y4=σ(w4y1+b4)=11+e−(w4y1+b4) |
| 5 | y5=σ(w5,2y2+w5,3y3+w5,4y4+b5)=11+e−(w5,2y2+w5,3y3+w5,4y4+b5) |
Y si volvemos a generar la formula completa de la neurona de la salida (es decir y5), la red neuronal queda de la siguiente forma:
y5=11+e−(w5,211+e−(w2x+b2)+w5,311+e−(w3x+b3)+w5,411+e−(w4x+b4)+b5)
Y esa si que es la verdadera función de nuestra red neuronal.
Y en la siguiente imagen se puede ver una animación esquemática de como funciona para predecir datos:
¿Y como sería ahora la programación en Keras de la red neuronal incluyendo la función de activación sigmoide en las neuronas?
1 2 3 4 |
model=Sequential()model.add(Dense(3, input_dim=1,activation="sigmoid"))model.add(Dense(1,activation="sigmoid"))model.compile() |
Mas información:
Recreando la red neuronal
Acabamos de ver que para la red neuronal
Y usando la función de activación sigmoide, la red neuronal que se obtiene es:
y5=11+e−(w5,211+e−(w2x+b2)+w5,311+e−(w3x+b3)+w5,411+e−(w4x+b4)+b5)
Pues bien, vamos a comprar el resultado de usar una red neuronal con el de la fórmula, para verificar que dar el mismo resultado.
Para ello vamos a crear con Keras la red neuronal, obtener los parámetros , crear la fórmula y comprar lo que retorna la red neuronal y la fórmula.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as npimport pandas as pdimport tensorflow as tffrom keras.models import Sequentialfrom keras.layers import Densefrom sklearn.datasets import load_irisiris=load_iris()x=iris.data[0:99,2]y=iris.target[0:99]np.random.seed(5)tf.random.set_seed(5)random.seed(5) model=Sequential()model.add(Dense(3, input_dim=1,activation="sigmoid"))model.add(Dense(1,activation="sigmoid"))model.compile(loss='mean_squared_error') |
Hemos creado el modelo y ahora vamos a entrenarlo con los datos.
1 |
model.fit(x, y,epochs=100) |
compile ya se dan valores aleatorios a los parámetros y luego con el método fit ya se entrena la red neuronal para que aprenda los valores correctos de los parámetros.
Ahora vamos a obtener todos los parámetros como hemos visto antes.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
def get_w(model,layer,neuron,index): layer=model.layers[layer] return layer.get_weights()[0][index,neuron] def get_b(model,layer,neuron): layer=model.layers[layer] return layer.get_weights()[1][neuron]w_2 =get_w(model,0,0,0)w_3 =get_w(model,0,1,0)w_4 =get_w(model,0,2,0)w_52=get_w(model,1,0,0)w_53=get_w(model,1,0,1)w_54=get_w(model,1,0,2)b_2 =get_b(model,0,0)b_3 =get_b(model,0,1)b_4 =get_b(model,0,2)b_5 =get_b(model,1,0)print(f"w_2={w_2}\nw_3={w_3}\nw_4={w_4}\nw_52={w_52}\nw_53={w_53}\nw_54={w_54}\nb_2={b_2}\nb_3={b_3}\nb_4={b_4}\nb_5={b_5}") |
- Y muestra por pantalla los valores de cada parámetro:
1 2 3 4 5 6 7 8 9 10 |
w_2=0.49803927540779114w_3=0.4119996428489685w_4=-0.46713322401046753w_52=0.8982692956924438w_53=-0.0004859123146161437w_54=0.3734080493450165b_2=-0.3795720934867859b_3=-0.20187339186668396b_4=-0.3774943947792053b_5=-0.3136947453022003 |
y5=11+e−(0.8982⋅11+e−(0.4980x−0.3795)+(−0.0004)⋅11+e−(0.4119x−0.2018)+0.3734⋅11+e−(−0.4671x−0.3774)+(−0.3136))
Por fin vamos a crear la fórmula que hará las predicciones pero usando únicamente los parámetros en vez de la red neuronal, para ello hemos creado la función predict_formula:
1 2 3 4 5 6 7 8 9 10 11 |
def sigmoid(z): return 1/(1 + np.exp(-z))def predict_formula(x): part1=w_52*sigmoid(w_2*x+b_2) part2=w_53*sigmoid(w_3*x+b_3) part3=w_54*sigmoid(w_4*x+b_4) part4=b_5 z=part1+part2+part3+part4 return sigmoid(z) |
Y ahora con todas las x que tenemos vamos a calcular el resultado de la red neuronal y lo mismo con la fórmula para ver si dan lo mismo:
1 2 |
y_predicho_red_neuronal=model.predict([x])y_predicho_formula=predict_formula(x) |
Para compararlos, los ponemos uno al lado del otro y así saldrán en parejas.
1 |
np.column_stack((y_predicho_red_neuronal,y_predicho_formula)) |
El resultado es éste:
array([[0.49011275, 0.49011275],
[0.49011275, 0.49011275],
[0.48533145, 0.48533144],
[0.49485764, 0.49485766],
[0.49011275, 0.49011275],
[0.50421923, 0.50421925],
[0.49011275, 0.49011275],
[0.49485764, 0.49485766],
[0.49011275, 0.49011275],
[0.49485764, 0.49485766],
[0.49485764, 0.49485766],
[0.49956134, 0.49956136],
[0.49011275, 0.49011275],
[0.47567996, 0.47567996],
[0.48051879, 0.48051877],
[0.49485764, 0.49485766],
[0.48533145, 0.48533144],
[0.49011275, 0.49011275],
[0.50421923, 0.50421925],
[0.49485764, 0.49485766],
[0.50421923, 0.50421925],
[0.49485764, 0.49485766],
[0.4708204 , 0.47082038],
[0.50421923, 0.50421925],
[0.51338053, 0.51338055],
......
[0.56985992, 0.56985994],
[0.59807748, 0.59807747],
[0.59807748, 0.59807747],
[0.59807748, 0.59807747],
[0.60083133, 0.60083131],
[0.5590229 , 0.5590229 ]])
¡¡¡¡¡¡Como podemos ver los números son iguales hasta el 7º decimal. Es decir que hemos comprobado que la fórmula coincide con la red neuronal!!!!!
Usando funciones de activación en Keras
Antes de ver los tipos de funciones de activación que hay , vamos a ver como se pueden usar el Keras ya que hay varias formas distintas de usarlas.
Para explicar como indicar la función de activación , vamos a usar como ejemplo usa función de activación llamada "ReLU".
- Usando un String con el nombre de la función de activación
1 |
"relu" |
- Usando una función de activación
1 |
tf.keras.activations.relu |
- Usando una capa de activación.
1 |
tf.keras.layers.ReLU() |
Las 3 formas de definir función de activación, se pueden usar en 2 sitios distintos. Como el parámetro activation o añadiendolo una nueva capa.
| Parámetro activation | Una nueva capa | |||||
|---|---|---|---|---|---|---|
| String |
| - | ||||
| Función de Activación |
| - | ||||
| Capa de Activación |
|
|
Parece que la forma más normal de definir la función de activación es simplemente poner el nombre pero hay funciones de activación que se pueden parametrizar , es decir que las puedes personalizar con un parámetro. La única forma de definir el parámetro en una capa de activación
1 2 |
model.add(Dense(3, input_dim=1))model.add(tf.keras.layers.ReLU(negative_slope=0.3)) |
Función a Capa
Si queremos seguir usando la función de activación pero dentro de una capa de activación podemos usar la clase tf.keras.layers.Activation o tf.keras.layers.Lambda
1 2 |
model.add(Dense(3, input_dim=1))model.add(tf.keras.layers.Activation(tf.keras.activations.relu)) |
1 2 |
model.add(Dense(3, input_dim=1))model.add(tf.keras.layers.Lambda(tf.keras.activations.relu)) |
Función parametrizada a Capa
Si queremos seguir usando la función de activación pero parametrizarla, podemos hacerlo transformandola en una capa de activación con la clase tf.keras.layers.Lambda
1 2 |
model.add(Dense(3, input_dim=1))model.add(tf.keras.layers.Lambda(lambda x: tf.keras.activations.relu(x,alpha=0.3))) |
alpha y en la capa se llama negative_slope. No se el porqué de dicha discrepancia
La lista competa en Keras de funciones de activaciones y capas de activación es la siguiente:
Tipos de funciones de activación en capas ocultas
Pasemos ahora a ver las distintas funciones de activación que se pueden usar en las capas ocultas. Por cuestiones didácticas, se han agrupado por similitud
- Sigmoide y Tangente Hiperbólica (tanh)
- Rectified Linear Unit (ReLU) y Leaky ReLU
- Exponential Linear Unit (ELU) y Scaled Exponential Linear Unit (SELU)
Mas información:
Sigmoide y Tangente Hiperbólica (tanh)
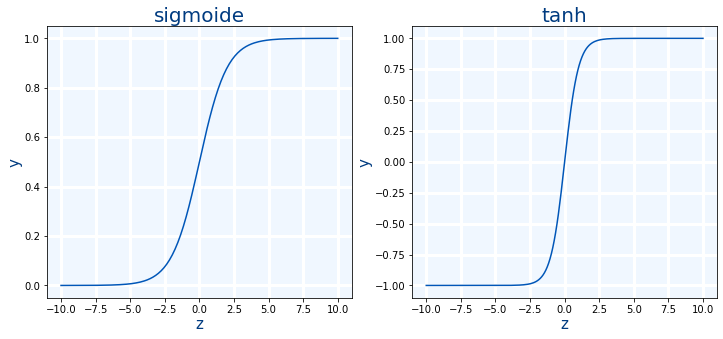
Son funciones de activación que tiene forma de "S". Se pueden usar en capas ocultas como de salida.
Sigmoide es la primera función de activación que se explica.Si rango de salida es de 0 a 1. Ya no se usa nunca en capas ocultas.
sigmoid(x)=11+e−x
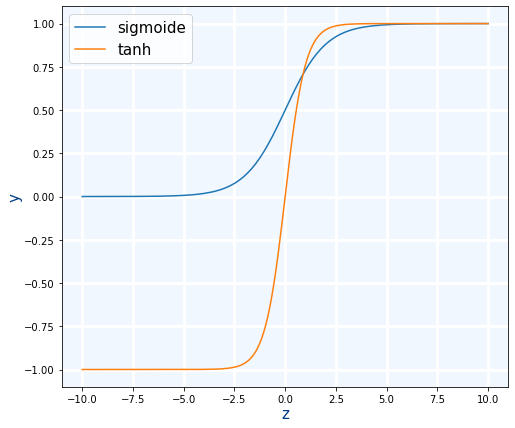
tanh es una mejora de la sigmoide. La ventaja es que su salida está centrada en 0 ya que salida está en el rango de -1 a 1. Las tarjetas gráficas actuales, pueden calcula la tanh en una única instrucción tanh.approx.f32
senh(x)=ex−e−x2 cosh(x)=ex+e−x2
tanh(x)=senh(x)cosh(x)=ex−e−x2:ex+e−x2=2⋅(ex−e−x)2⋅(ex+e−x)=ex−e−xex+e−x
Un problema de estas dos funciones es que para valores muy grandes o muy pequeños dan siempre el mismo valor.
- Uso en Keras: Sigmoide
1 2 |
model.add(Dense(3, activation="sigmoid"))model.add(Dense(3, activation=tf.keras.activations.sigmoid)) |
- Uso en Keras: Tangente Hiperbólica
1 2 |
model.add(Dense(3, activation="tanh"))model.add(Dense(3, activation=tf.keras.activations.tanh)) |
Mas información:
ReLU y Leaky ReLU
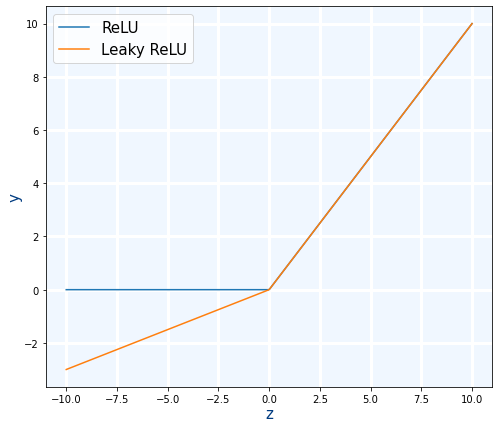
ReLU: Es mejor que las anteriores ademas de ser muy rápida ya que prácticamente no hace falta calcular nada. Sin embargo tiene un problema con valores negativos que siempre retorna 0.
ReLu(x)={x>0xx≤00
Leaky ReLU: Es una mejora de ReLU al hacer que los valores negativos tengan un valor menor que cero. Sigue siendo muy rápida de calcular.
- Ese valor negativo de define en función de un parámetro llamado "alpha" α.
- El rango de su valor es α=]0,1[
- Si α=0, se comportará como ReLU
- Si α=1, se comportará como si no hubiera función de activación (o también se puede decir que la función de activación es linear y=z).
- El valor por defecto en Keras es α=0.3
LeakyReLU(x)={x>0xx≤0αx
- Uso en Keras: ReLU
1 2 3 |
model.add(Dense(3, activation="relu"))model.add(Dense(3, activation=tf.keras.activations.relu))model.add(Dense(3, activation=tf.keras.layers.ReLU())) |
- Uso en Keras: Leaky ReLU. Por defecto α=0.3
1 2 3 |
model.add(Dense(3, activation="LeakyReLU"))model.add(Dense(3, activation=tf.keras.layers.LeakyReLU()))model.add(Dense(3, activation=tf.keras.layers.LeakyReLU(alpha=0.2))) |
Mas información:
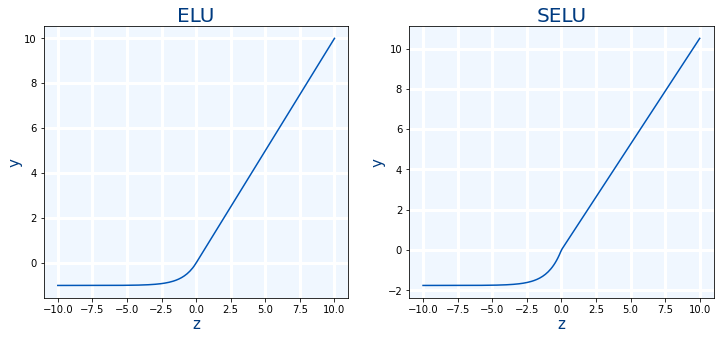
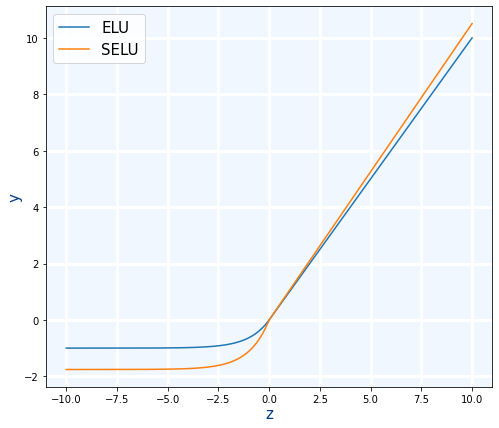
ELU y SELU
Son unas mejora de las anteriores pero tienen que problema de que son muchas lentas de calcular.
ELU:Es similar a ReLU pero cuando cuando la entrada es negativa, hace una caída mas suave para luego estabilizarse. Tiene un parámetro para controlar la caída llamado alfa cuyo valor por defecto α=1
ELU(x)={x>0xx≤0α(ex−1)
SELU: Es similar a ELU pero mejor que ella.Lo que hace es modificar ligeramente la formula estableciendo el valor de α=1.67326324 y multiplicando la salida por el factor de escala scale=1.05070098. Por lo tanto al ser casi como ELU por lo que su velocidad es prácticamente la misma y ser mejor que ELU se recomienda usar SELU. Sin embargo para que SELU sea mejor que ELU se tienen que cumplir una serie de precondiciones:
- Las entradas deben estar normalizadas. Media 0 y desviación 1.
- La inicialización de los pesos debe ser Lecun Normal.
kernel_initializer="lecun_normal" - No se puede usar en redes recurrentes.
- Las capa deben ser densas
SELU(x)=1.05070098⋅{x>0xx≤01.67326324⋅(ex−1)
- Uso en Keras: ELU. α=0.1 por defecto
1 2 3 |
model.add(Dense(3, activation="elu"))model.add(Dense(3, activation=tf.keras.activations.elu))model.add(Dense(3, activation=tf.keras.layers.ELU(alpha=0.2))) |
- Uso en Keras: SELU
1 2 |
model.add(Dense(3, activation="selu"))model.add(Dense(3, activation=tf.keras.activations.selu)) |
Mas información:
Selección de función de activación
¿Que función de activación deberíamos usar entonces para las capas ocultas?
Según Hands-On Machine Learning with Scikit-Learn and TensorFlow:
SELU>ELU>LeakyReLU>ReLU>Tanh>Sigmoid
Sin embargo según Activation functions you might have missed se debería seguir este esquema:
Pero mi opinión es la siguiente:
- Deberíamos empezar siempre probando con
ReLUyLeaky ReLUya que son las más rápidas y en general funcionan bien. - Si
ReLUyLeaky ReLUno dan un resultado lo suficientemente bueno, probar conSELUoELU - El último lugar probar con
swish - Nunca deberíamos usar ni
SigmoideniTanha menos que no nos quede mas remedio
Tipos de funciones de activación en la capa de salida
En el apartado anterior hemos visto las funciones de activación que se usan en las capas ocultas, ahora vamos a ver las que se pueden usar en la capa de salida.
- Linear
- Sigmoide
- Softmax
Los problemas que resuelven las redes neuronales se suelen clasificar en:
- Problemas de regresión: En los que se calcula un número.Ejemplo: El consumo de gasolina de un coche en función del peso, cilindrada y altura.
- Problemas de clasificación: En lo que hay que clasificar los datos entrada: Ejemplo: Dado una imagen indicar si es de una persona sonriendo.
Según el tipo de problema se usarán unas funciones u otras:
- Problemas de regresión
- Linear
- Problemas de clasificación
- Sigmoide
- Softmax
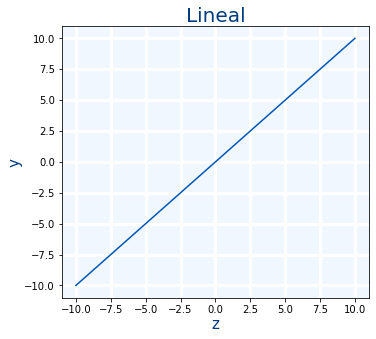
Lineal
La función de activación lineal es como si realmente no hubiera función de activación.
lineal(x)=x
La forma de usarla en keras es simplemente no diciendo nada sobre la función de activación en la capa de salida.
La función lineal se usa en problemas de regresión, cuando la salida puede ser cualquier número. Ejemplos de ello son:
- El dinero que vamos a ganar
- La temperatura que va a hacer en grados centígrados °C.
- Cuanto va a subir o bajar la bolsa
- La cantidad de combustible que consume un coche
- Etc.
- Uso en Keras
1 2 |
model.add(Dense(3, activation="linear"))model.add(Dense(3, activation=tf.keras.activations.linear)) |
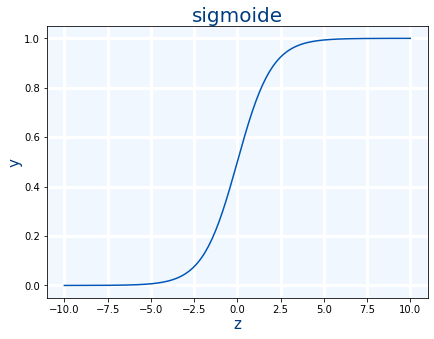
Sigmoide
Ya hemos visto la función de activación sigmoide
sigmoide(x)=11+e−x
La función Sigmoide se usa en problemas de clasificación, cuando la salida es una probabilidad entre 0 y 1. Ejemplos de ello:
- La probabilidad de que una foto sea un gato
- La probabilidad de que una foto sea un perro
- La probabilidad de que una foto sea una vaca
- La probabilidad de que haya que comprar mañana acciones de la empresa X.
- La probabilidad de que haya que comprar mañana acciones de la empresa Y.
- La probabilidad de que haya que comprar mañana acciones de la empresa Z.
Es decir se puede usar para clasificar entre 2 opciones pero también se puede usar cuando son más de dos opciones pero que no sean excluyentes entre ellas.
y_true deben estar preparados para ello. Por ejemplo en la red de las flores, cada flor es un número. Pero deberíamos usar la función OneHotEncoder para transformarlo en columnas distintas para cada tipo de flor
- Uso en Keras
1 2 |
model.add(Dense(3, activation="sigmoid"))model.add(Dense(3, activation=tf.keras.activations.sigmoid)) |
Softmax
Se usa en problemas de clasificación. La función Softmax no es fácil de representar gráficamente pero vamos a intentar explicarla.
En vez de aplicarse a una única neurona se aplica a todas las neuronas de una capa. Es similar a la sigmoide pero lo que hace es que la probabilidad de todas las salidas de la capa debe sumar 1.
softmax(xi)=exin∑j=0exj
Siendo xi la entrada la la neurona i-esioma y siendo xj todas las entradas a todas las neuronas de la capa habiendo n neuronas en la capa. Por lo que xi corresponde con uno de los valores de xj
Ejemplos de ello:
- La probabilidad de que una foto sea un gato o un perro o una vaca
- La probabilidad de que haya que comprar mañana acciones de la empresa X o de la Y o de la Z.
La explicación es similar a la sigmoide pero vamos a ver con ejemplos las diferencias.
- Ejemplo de red que dice si una foto tiene una jarrón, una mesa o un perro.
En este caso la red neuronal tendría 3 neuronas en la capa de salida. Una para cada uno de los objetos que puede detectar.
¿Pueden las 3 neuronas sacar cada una un 1 porque están los 3 objetos? En ese caso debemos usar la función sigmoide.
- Ejemplo de red que dice si una foto es de un jarrón, una mesa o un perro.
En este caso la red neuronal también tendría 3 neuronas en la capa de salida. Una para cada uno de los objetos que puede detectar.
¿Pueden las 3 neuronas sacar cada una un 1 porque están los 3 objetos? No porque solo puede ser uno de los 3 objetos, por lo tanto hay que usar la función de activación softmax ya que de esa forma indicamos cual de los 3 objetos es mas probable pero la suma de las 3 probabilidades debe sumar 1.
Es decir que si las neuronas de la capa de salida son resultados independientes de las otras neuronas , usamos sigmoide pero si sus salidas están relacionadas con las otras neuronas, usaremos softmax
y_true deben estar preparados para ello. Por ejemplo en la red de las flores, cada flor es un número. Pero deberíamos usar la función LabelBinarizer para transformarlo en columnas distintas para cada tipo de flor
1 2 3 4 5 6 |
from sklearn.preprocessing import LabelBinarizery=iris.targetlabel_binarizer = LabelBinarizer()label_binarizer.fit(range(max(y)+1))y = label_binarizer.transform(y) |
- Uso en Keras
1 2 |
model.add(Dense(3, activation="softmax"))model.add(Dense(3, activation=tf.keras.activations.softmax)) |
Para finalizar vamos a mostrar en una tabla resumen cuando se usa función de activación
Para acabar vamos a ver una tabla con la relación entre las funciones de activación usadas en la salida de una red neuronal y la función de coste que se podría usar.
| Problema | Función de Activación a la salida |
|---|---|
| Regresión | Lineal |
| Clasificación con 2 posibles valores | Sigmoide |
| Clasificación con más de 2 posibles valores NO excluyentes entre si | Sigmoide |
| Clasificación con más de 2 posibles valores SI excluyentes entre si | Softmax |
Uno se puede preguntar en redes en las solo queremos saber si es positivo/negativo, es decir con dos valores, porqué en vez de usar una única neurona con sigmoide, no usamos softmax con 2 valores. ¿Sería lo mismo? Pues vamos a desarrollarlo.
- Imaginemos una única neurona que acaba en sigmoide.
z1:Es la salida de la parte lineal de la única neuronay1:Es la salida de la única neuronay1=sigmoid(z1)=11+e−z1
- Ahora vamos a tener 2 neuronas de forma que la primera neurona de el mismo resultado que cuando solo hay una neurona
z1:Es la salida de la parte lineal de la 1º neuronay1:Es la salida de la 1º neuronay1=softmax(z1)=ez1ez1+ez2
z2:Es la salida de la parte lineal de la 2º neuronay2:Es la salida de la 2º neuronay2=softmax(z2)=ez2ez1+ez2
- Además se debe cumplir que
y1+y2=1
Ya que la probabilidad de ser positivo o ser negativo debe sumar 1.
- Como ambas redes deben tener el mismo resultado en la 1º reurona se cumple que
11+e−z1=ez1ez1+ez2
- Y ahora vamos a despejar cuando debe valer z2 para que se cumple esa igualdad y para ello multiplicamos en cruz
ez1+ez1−z1=ez1+ez2
ez1+e0=ez1+ez2
ez1+1=ez1+ez2
1=ez2
ln1=lnez2
z2=0
Por lo tanto:
y1=ez1ez1+1=11+e−z1
Es decir que la 2º neurona siempre debe valer 0 en la parte lineal. z2=0
- ¿Pero que valor tendrá realmente a la salida de la 2º neurona?
y2=softmax(z2)=ez2ez1+ez2
y2=e0ez1+e0
y2=11+ez1
- Pero, ¿es ese valor realmente el complementario de y1. Es decir ¿y1+y2=1?
y1=11+e−z1y2=11+ez1
y1+y2=11+e−z1+11+ez1=
1+ez1+1+e−z1(1+e−z1)(1+ez1)=
2+ez1+e−z11+e−z1+ez1+ez1−z1=
2+ez1+e−z11+e−z1+ez1+e0= 2+ez1+e−z11+e−z1+ez1+1=
2+ez1+e−z12+ez1+e−z1=1
Mas información:
Guardando modelos a disco
Una vez tenemos la red neuronal entrenada, la podemos guardar a disco para poder usarla en otro programa.
- Para guardar la red
1 2 3 4 5 6 |
model=Sequential()model.add(Dense(10, activation="sigmoid",input_dim=2))model.compile(loss="mse")history=model.fit(x_train,y_train,validation_data=(x_test,y_test),epochs=10,verbose=False)model.save('my_red_neuronal.keras') |
- Para cargar la red en otro programa
1 |
model=tf.keras.models.load_model('my_red_neuronal.keras') |
- Si el modelo al crearse usó funciones personalizadas, se debe usar el parámetro
custom_objects. Por ejemplo si se usó la funciónspecificityse debe cargar:
1 |
model=tf.keras.models.load_model('my_red_neuronal.keras',custom_objects={"specificity": specificity}) |
Más información:
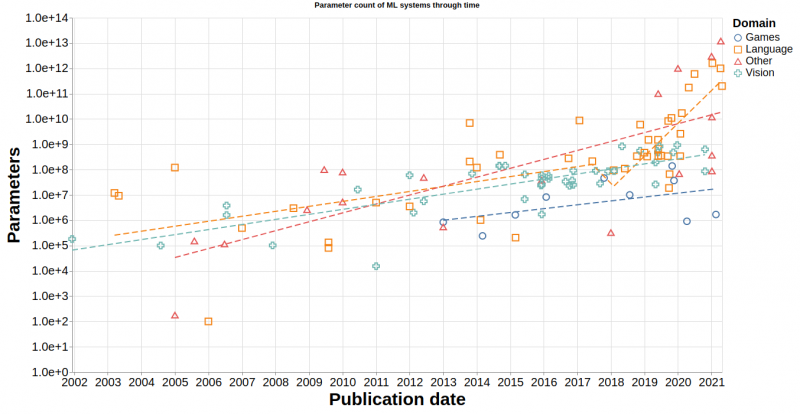
Redes Neuronales Famosas
Antes hemos vito el tamaño de una red neuronal, ¿Que tamaño tienen las redes neuronales mas famosas? Lo podemos ver en el siguiente gráfico:
| Año | Red | Nº Parámetros | Creador |
|---|---|---|---|
| 2004 | Lira | 100.000 | |
| 2007 | λ-WASP | 490.000 | |
| 2008 | Semantic Hashing | 2.600.000 | |
| 2010 | NORB | 16.000.000 | |
| 2012 | AlexNet | 60.000.000 | |
| 2014 | Seq2Seq | 380.000.000 | |
| 2017 | MoE | 8.700.000.000 | |
| 2019 | DLRM-2020 | 100.000.000.000 | |
| 2020 | GPT-3 | 175.000.000.000 | OpenAI |
| 2021 | Gopher | 280.000.000.000 | DeepMind (Google) |
| 2021 | Megatron-Turing NLG | 530.000.000.000 | Microsoft & NVIDIA |
| 2021 | DLRM-12T | 12.000.000.000.000 |
¿Y con que hardware se hace todo eso? La red neuronal StyleGAN3 que genera imágenes de caras , tiene 530 mil millones de parámetros. NVIDIA uso 560 ordenadores DGX A100, teniendo cada uno de ellos con 8 tarjetas gráficas A100 con 80GB de RAM cada una. Por lo tanto se usaron 4.480 gráficas y un total de 358.400 GB de memoria.
¿Y cuales son las empresas punteras en inteligencia artificial?: Artificial intelligence researchers rank the top A.I. labs worldwide
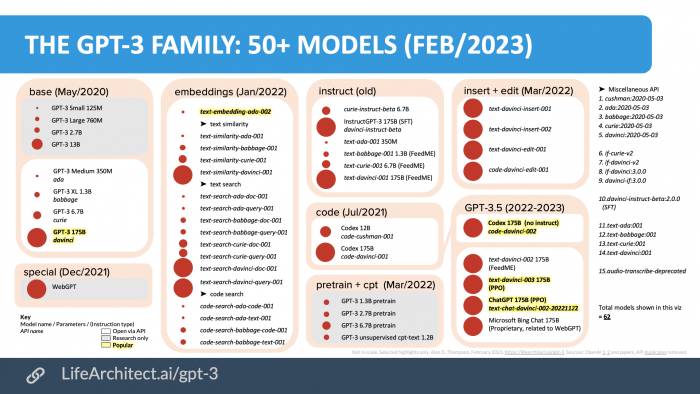
ChatGPT forma parte de la familia de modelos basados en GPT-3 pero especializado en conversaciones como se puede ver en la siguiente imagen:
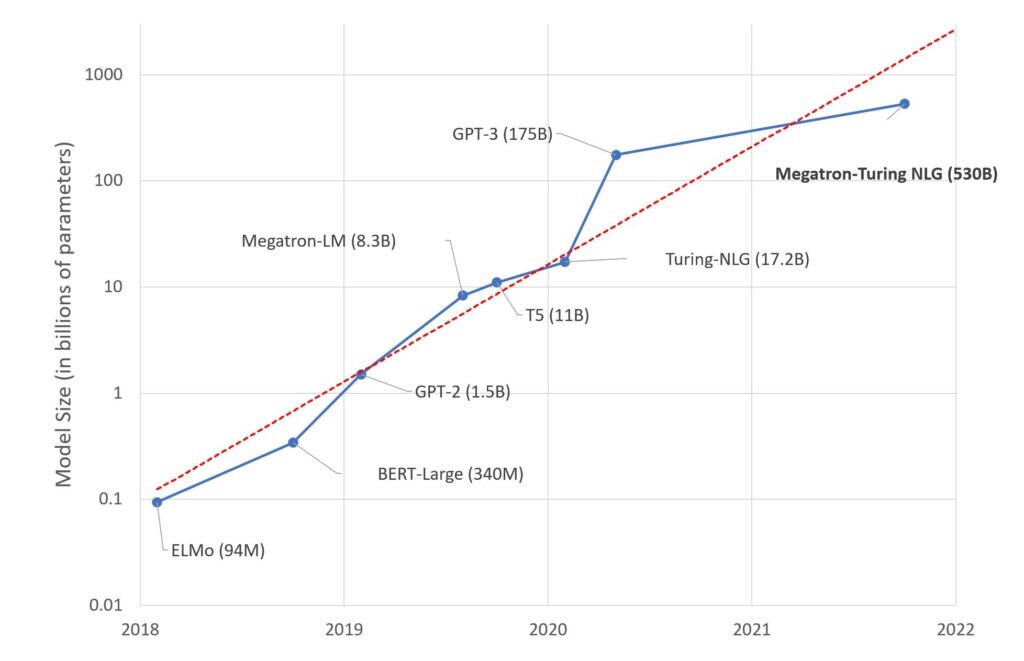
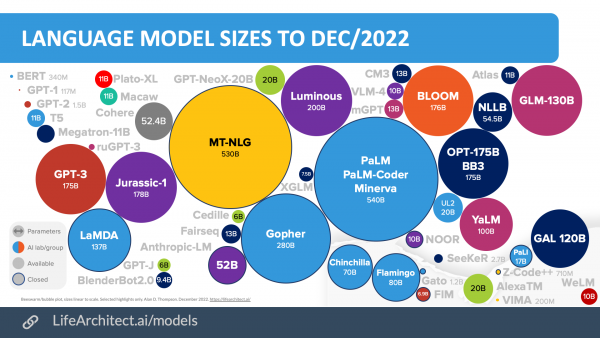
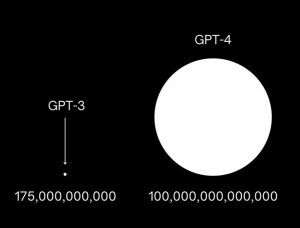
Además ChatGPT no es de los modelos con más parámetros como podemos ver a continuación:
Por último vemos el tamaño que tendrá GPT4:
Mas información:
- Ordenador NVIDIA DGX A100:
- ChatGPT
Ejercicios
Ejercicio 1.A
Dada la siguiente red neuronal:
- Indica las fórmulas de cada una de las neuronas suponiendo que no hay función de activación
- Indica el Nª de capas
- Entrada
- Salida
- Ocultas
- Para cada neurona
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Para cada capa
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Para toda la red
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Crea el código en Keras de la red neuronal.
- Muestra el resumen de la red en Keras y comprueba que coincide con lo calculado
- Muestra el grafico de la red en Keras y comprueba que coincide con lo calculado
- Imprime por pantalla el valor de cada uno de los pesos
Ejercicio 1.B
Modifica la red anterior pero ahora.
- Indica las fórmulas de cada una de las neuronas sabiendo que la función de activación de todas la neuronas es
sigmoid.
Ejercicio 1.C
Modifica la red anterior pero ahora.
- Indica las fórmulas de cada una de las neuronas sabiendo que la función de activación de todas la neuronas es
tanh.
Ejercicio 2.A
Dada la siguiente red neuronal:
- Indica las fórmulas de cada una de las neuronas suponiendo que no hay función de activación
- Indica el Nª de capas
- Entrada
- Salida
- Ocultas
- Para cada neurona
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Para cada capa
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Para toda la red
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Crea el código en Keras de la red neuronal.
- Muestra el resumen de la red en Keras y comprueba que coincide con lo calculado
- Muestra el grafico de la red en Keras y comprueba que coincide con lo calculado
- Imprime por pantalla el valor de cada uno de los pesos
Ejercicio 2.B
Modifica la red anterior pero ahora.
- Indica las fórmulas de cada una de las neuronas sabiendo que la función de activación de todas la neuronas es
sigmoid.
Ejercicio 2.C
Modifica la red anterior pero ahora.
- Indica las fórmulas de cada una de las neuronas sabiendo que la función de activación de todas la neuronas es
tanh.
Ejercicio 3
Dada la siguiente red neuronal:
- Indica el Nª de capas
- Entrada
- Salida
- Ocultas
- Para cada capa
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Para toda la red
- Indica el nº parámetros
- Indica en nº de entradas
- Indica en nº de salidas
- Crea el código en Keras de la red neuronal.
- Muestra el resumen de la red en Keras y comprueba que coincide con lo calculado
- Muestra el grafico de la red en Keras y comprueba que coincide con lo calculado
Ejercicio 4.A
Dada la siguiente red neuronal:
- Indica las fórmulas de cada una de las neuronas sabiendo que la función de activación es
sigmoiden las 2 capas - Crea la red en Keras y obtén el valor de los parámetros.
- Modifica la fórmula poniendo el valor de los parámetros.
- Aplica la fórmula con los valores de entrada
4.7y1.3y calcula el resultado. - Usando el método
predictcalcula lo que da la red de keras y comprueba que coincide con el calculado.
¡¡¡Acabas de comprobar como funciona internamente una red neuronal!!!
Ejercicio 4.B
Repite el ejercicio anterior pero antes de obtener los parámetros, entrena la red con los valora del largo del sépalo y el largo del pétalo.
Y comprueba si los resultados coinciden con todas las flores de tipo 0 y tipo 1, para ello deberás hacer un pequeño programa que calcule el resultado de la fórmula.
Ejercicio 5.A
Con los datos de las flores y la configuración de neuronas [2,4,8,4,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación tangente hiperbólica indicando la función de activación como un
string - Usen la función de activación tangente hiperbólica indicando la función de activación como una
función de python
Indica además que inicializador usarías con ella
Ejercicio 5.B
Con los datos de las flores y la configuración de neuronas [2,4,8,4,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación ReLU indicando la función de activación como un
string - Usen la función de activación ReLU indicando la función de activación como una
función de python - Usen la función de activación ReLU indicando la función de activación como una
clase de python
Indica además que inicializador usarías con ella
Ejercicio 5.C
Con los datos de las flores y la configuración de neuronas [2,4,8,4,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación LeakyReLU indicando la función de activación como un
string(No se puede) - Usen la función de activación LeakyReLU indicando la función de activación como una
función de python(No se puede) - Usen la función de activación LeakyReLU indicando la función de activación como una
clase de python - Usen la función de activación LeakyReLU con un valor de α=0.03 indicando la función de activación como una
clase de python
Indica además que inicializador usarías con ella
Ejercicio 5.D
Con los datos de las flores y la configuración de neuronas [2,4,8,4,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación SELU indicando la función de activación como un
string - Usen la función de activación SELU indicando la función de activación como una
función de python
Indica además que inicializador usarías con ella
Ejercicio 5.E
Con los datos de las flores y la configuración de neuronas [2,4,8,4,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación ELU con un valor de α=0.2
Indica además que inicializador usarías con ella
Ejercicio 5.F
Con los datos de las flores y la configuración de neuronas [2,4,8,4,2,1] crea una red neuronal cuyas capas ocultas:
- Usen la función de activación tangente hiperbólica indicando la función de activación como un
string - Usen la función de activación ReLU indicando la función de activación como una
función de python - Usen la función de activación LeakyReLU con un valor de α=0.35 indicando la función de activación como una
clase de python - Usen la función de activación SELU indicando la función de activación como un
string - Usen la función de activación ELU con un valor de α=0.25
Indica además que inicializador usarías con ella
Ejercicio 6.A
Con los datos del cáncer de mama crea una red neuronal de forma que
- Tenga las siguientes capas
[2,5,10,15,20,15,10,5,2,1] - Se entrenará durante 100 épocas
- En las capas ocultas se usará la función de activación "SeLU"
- Haz 3 gráficas con la función de pérdida comparando los inicializadores:
lecun_normalhe_normalglorot_normal
¿Que dice la teoría de cual se debería haber usado? ¿Ha habido alguna diferencia?
Ejercicio 6.B
Repita el ejercicio anterior pero ahora con las siguientes capas:
[5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,70,65,60,55,50,45,40,35,30,25,20,15,10,5,1]
¿Que dice la teoría de cual se debería haber usado? ¿Ha habido alguna diferencia?
Ejercicio 7
Con los datos del cáncer de mama crea una red neuronal con las siguientes capas [16,32,64,127,64,32,16,8,1] variando cada vez la función de activación y mostrando una gráfica con su función de perdida. el nº de épocas será de 100. Y se usará el inicializador glorot_uniform
- sigmoid
- tanh
- ReLU
- Leaky ReLU
- ELU
- SELU
Responde:
- ¿Cuales son las que dan un mejor resultado?
Ejercicio 8
Para cada uno de los problemas siguientes de redes neuronales:
- Obtener el consumo de un coche según las distintas condiciones climáticas, la carretera y el tipo de coche
- Averiguar si un paciente tendrá diabetes en el futuro según una serie de analíticas que se han ido haciendo a lo largo de su vida.
- Distinguir entre 5 tipos de vino según distintas características del vino
- Indicar las variedades de olivas que lleva un aceite y su proporción según el análisis químico que se le hace al aceite.
- Indicar si una compra con tarjeta es fraudulenta
- Averiguar a que partido político ha votado una persona
- Averiguar la distancia a la que se encuentra una estrella según diversas fotos que se van sacando de ella con telescopios.
- Entre 8 tipos distintos de canceres y dada la foto de las células de una persona averiguar los cánceres que puede tener
- Saber el tipo de tiburón según el sonido que hace bajo el agua al desplazarse
- Calcular la ubicación de los objetivos a destruir por un tanque según los sensores proporcionados por el tanque
- Averiguar la cifra que se ha escrito una persona a mano.
Indica:
- La función de activación que usarías en la última capa
- El Nº de neuronas de la última capa
Ejercicio 9.A
Crea y entrena una red neuronal con los datos de las flores pero ahora ya deberás tener en cuenta los 3 tipos de flor.
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- ¿Cuantas neuronas tiene la última capa?
Ejercicio 9.B
Crea y entrena una red neuronal que averigüe el tipo de un vino. Los datos los obtendrás con la función load_wine.
1 |
from sklearn.datasets import load_wine |
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- ¿Cuantas neuronas tiene la última capa?
Ejercicio 9.C
Crea y entrena una red neuronal que averigüe el dígito que ha escrito una persona. Los datos los obtendrás con la función load_digits.
1 |
from sklearn.datasets import load_digits |
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- ¿Cuantas neuronas tiene la última capa?
Ejercicio 9.D
Crea y entrena una red neuronal que averigüe la "cantidad" (es un número) de diabetes que tendrá un paciente. Los datos los obtendrás con la función load_diabetes.
1 |
from sklearn.datasets import load_diabetes |
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- ¿Has conseguido que haya un error bajo?
Ejercicio 10
Crea y entrena una red neuronal que averigüe el tipo de vino. Los datos los obtendrás con la función load_wine.
1 |
from sklearn.datasets import load_wine |
Deberás:
- Probar con varias funciones de activación en las capas ocultas para ver cual es la mejor.
- Elegir adecuadamente la función de activación de la capa de salida
- Deberás también probar para cada una de las funciones de activación las siguientes estructuras de red:
| Nº Neuronas en cada capa |
|---|
| 2,4,3 |
| 4,8,3 |
| 8,16,8,3 |
| 4,8,4,3 |
| 8,16,8,3 |
| 16,32,16,8,3 |
| 32,64,32,8,3 |
| 64,128,64,8,3 |
| 8,16,32,64,32,16,8,3 |
- La colocación de las distintas gráficas serán la siguiente:
- En cada columna estarán las gráficas de cada función de activación
- En cada fila estarán las gráficas de cada arquitectura de red